
var计量模型.pdf

as****16



亲,该文档总共22页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料
var计量模型.pdf
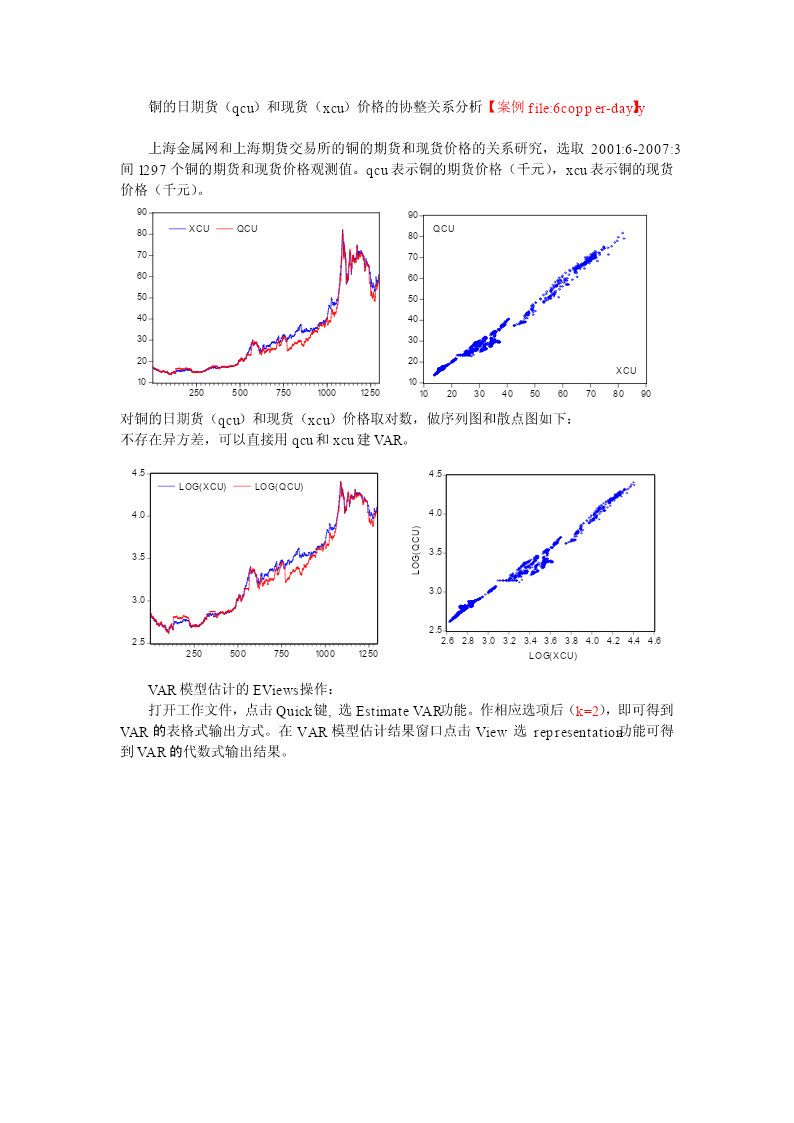
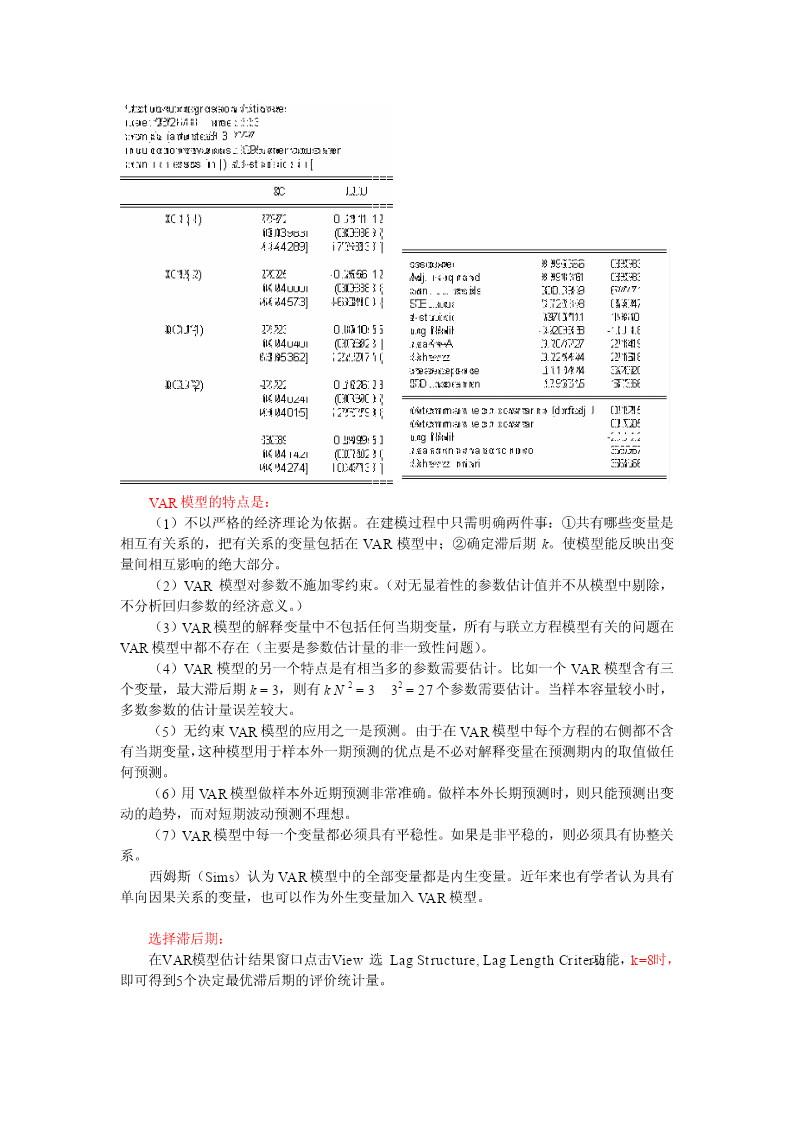
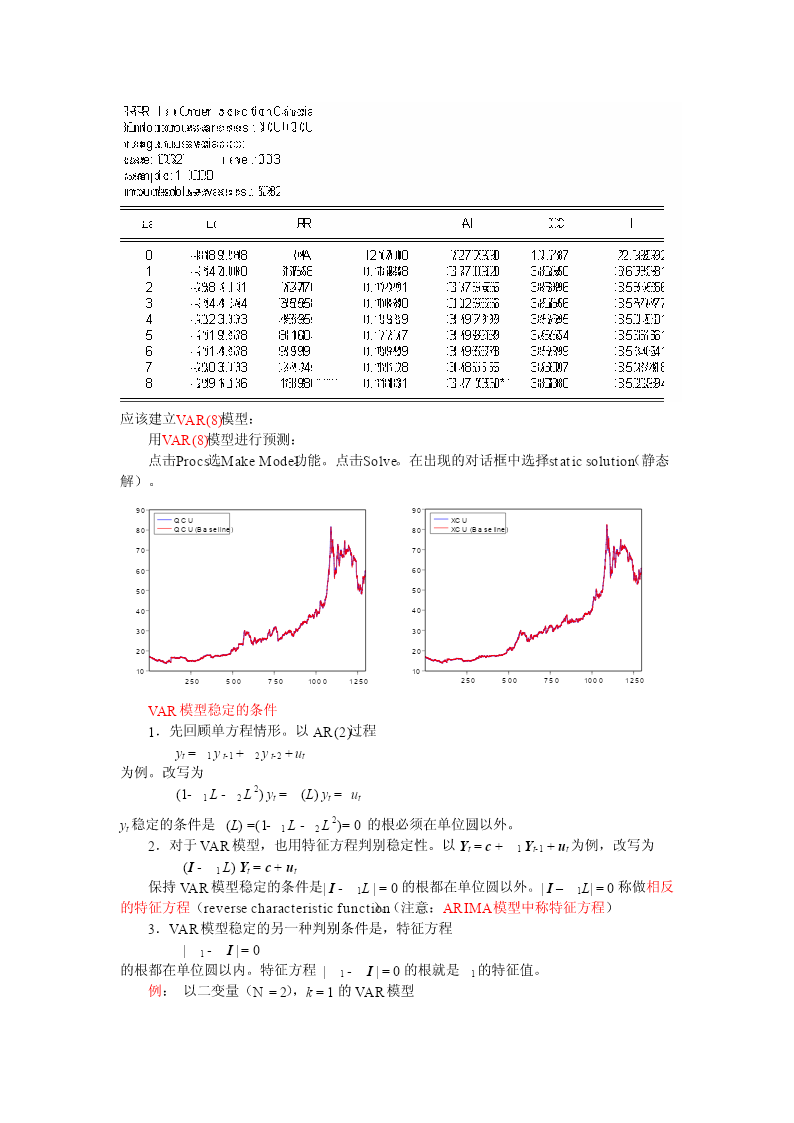
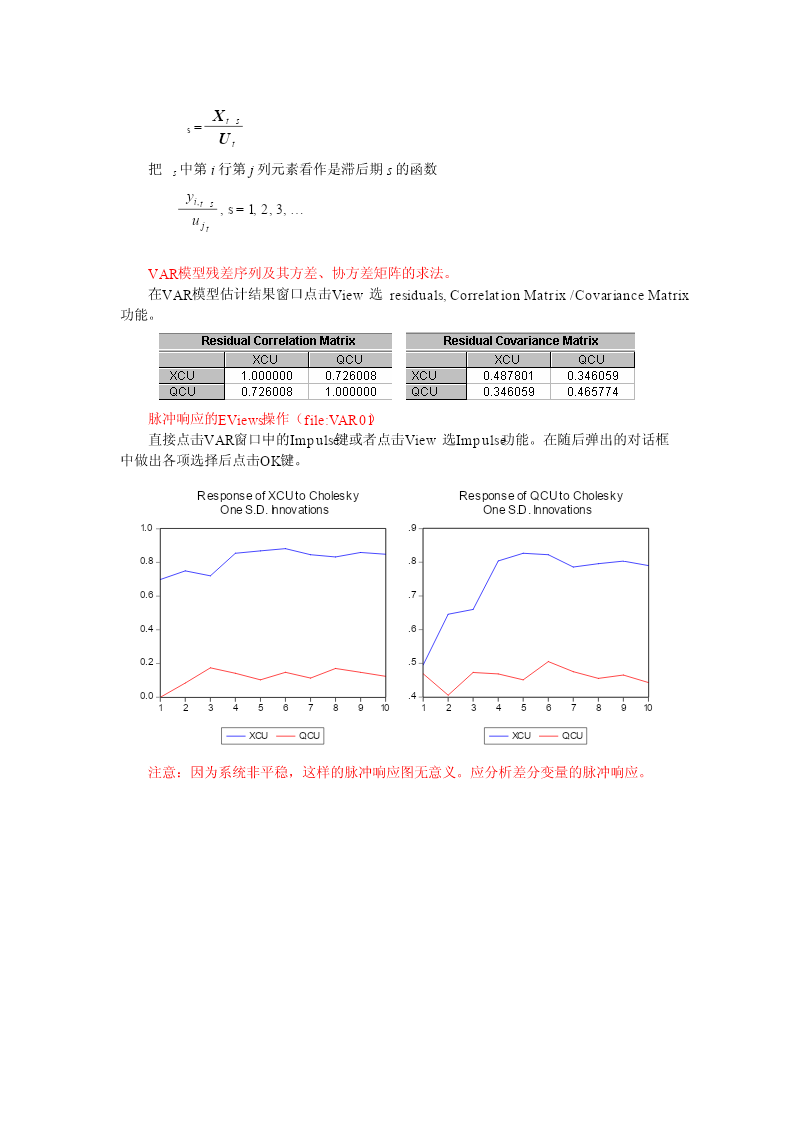
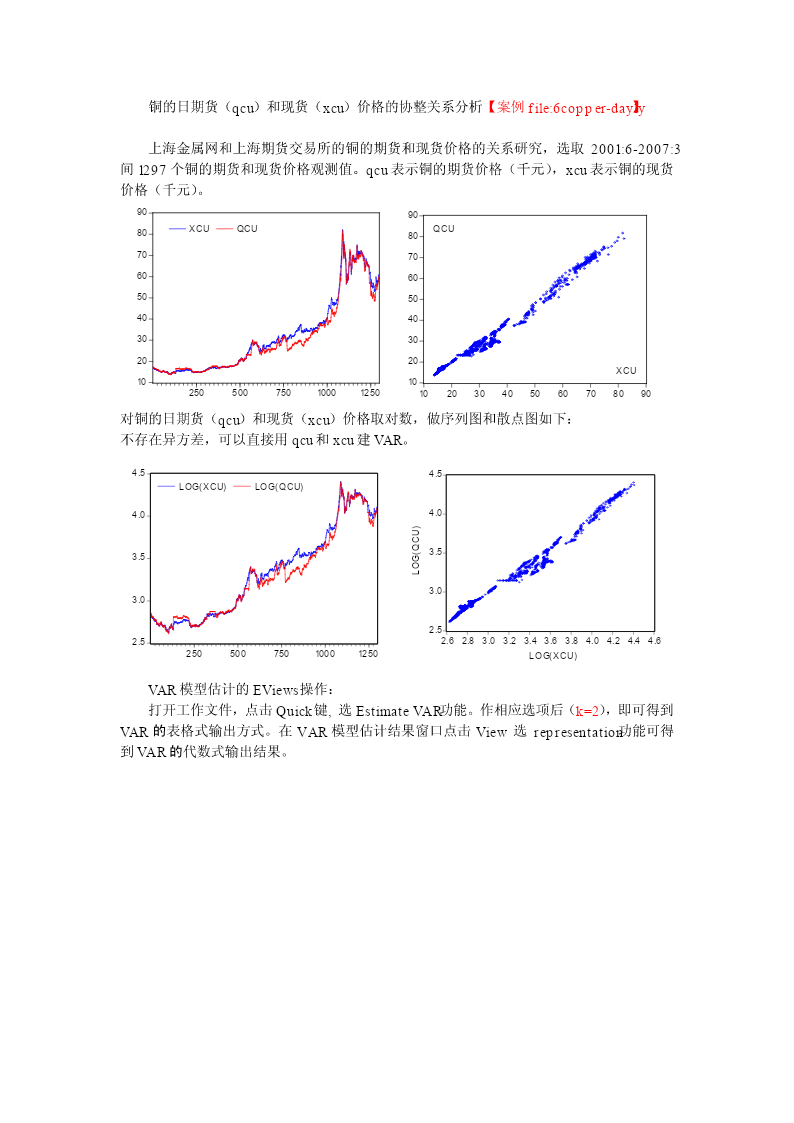
铜的日期货(qcu)和现货(xcu)价格的协整关系分析【案例file:6copper-dayly】上海金属网和上海期货交易所的铜的期货和现货价格的关系研究,选取2001:6-2007:3间1297个铜的期货和现货价格观测值。qcu表示铜的期货价格(千元),xcu表示铜的现货价格(千元)。9090XCUQCUQCU8080707060605050404030302020XCU101025050075010001250102030405060708090对铜的日期货(qcu)和现货(xcu)价格取对数,做序列

以VaR风险计量模型.ppt
以VaR風險計量模型衡量台灣指數期貨的避險效果專題大綱第一章緒論1.1研究動機1.2研究目的1.3研究方法資料蒐集1.5研究限制第二章文獻探討表2.1與共同基金相關之文獻表2.2與指數相關之文獻表2.3與匯率相關之文獻表2.4其他類別-1表2.4其他類別-2第三章研究方法3.1風險值的計算法歷史模擬法找出過去一段時間(T天)每日歷史價格時間序列。P1,P2,P3,……,Pr拔靴法求1000個亂數→(rand()*100)複製1000個亂數蒙地卡羅法求亂數1000個,複製亂數1000筆變異數-共變異數法求出

VaR计量模型分析案例.pdf
沪市动态VaR计量模型分析案例西南财经大学统计学院马丹一、案例背景金融风险是指由于经济活动的不确定性而导致资金在筹措和运用中遭受损失的可能性。在20世纪80年代以前,金融机构所面临的风险还主要是信用风险。然而,近20多年来金融市场发生了重大变化,全球化的证券市场迅猛发展,资产证券化的趋势越来越强,外汇交易和衍生品交易成了金融市场交易的重要组成部分。这使得金融机构所面临的主要风险已从信用风险转向了市场风险。市场风险度量的方法有多种,VaR(Value-at-Risk)方法是目前金融市场风险测量的主流方法。V

VaR计量模型在A商业银行应用的案例研究.docx
VaR计量模型在A商业银行应用的案例研究随着金融市场的快速发展和金融产品的不断创新,商业银行的风险管理也面临着愈加复杂的挑战。在这种背景下,如何利用有效的风险管理工具来降低银行的风险,成为了商业银行重要的任务之一。其中,VaR(ValueatRisk)计量模型被广泛应用于商业银行的风险管理中。VaR是一种通过量化风险的方法,评估在给定置信水平下的最大可能亏损额。VaR可以帮助商业银行拟定风险管理策略,制定合理的资产配置和底仓控制,从而降低银行的风险水平。本文以A商业银行为例,对其VaR计量模型的应用进行研

VAR模型.ppt
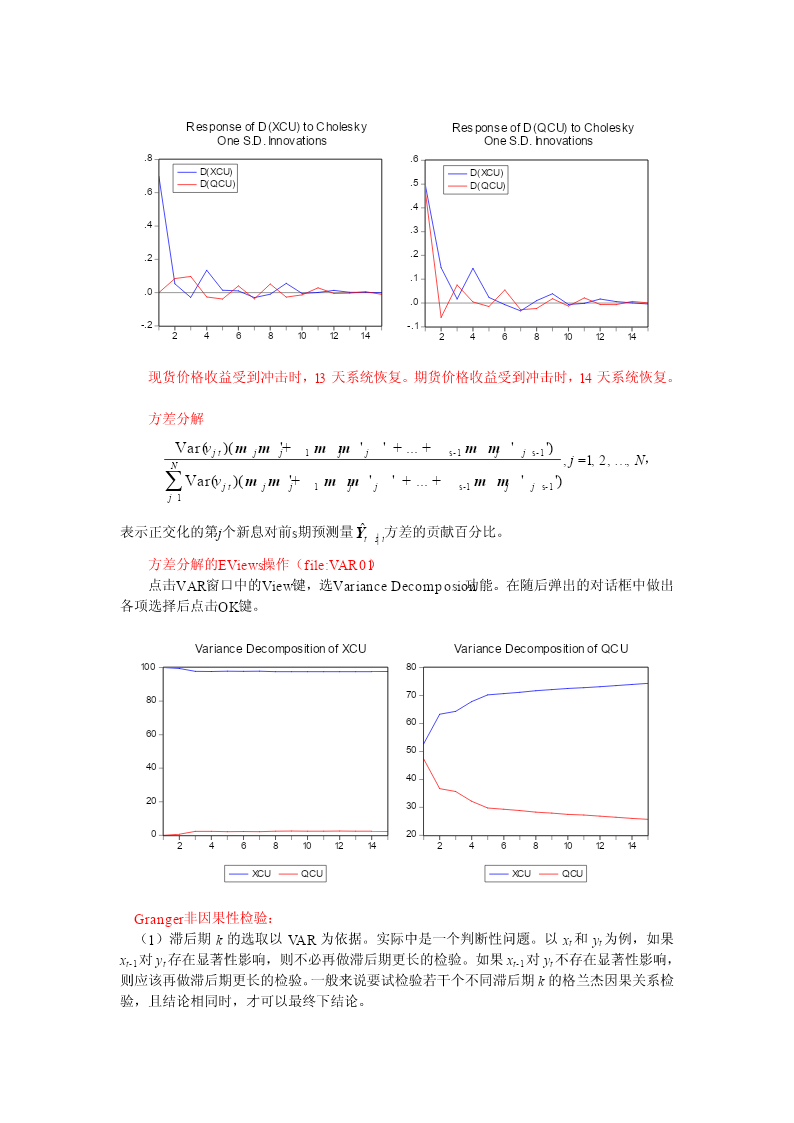
第5讲VAR模型本讲内容一、VAR模型介绍二、VAR模型的估计与相关检验三、格兰杰因果关系检验四、脉冲响应分析
