
小孩拉玩具问题数学模型.doc

qw****27




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

小孩拉玩具问题数学模型.doc
小孩和玩具的问题图1ABC图2解:假设小孩拉的玩具如图1所示,由于整个推拉过程中(图2),玩具走的轨迹,只与C在地面上的投影点B的轨迹有关。所以我们把模型简化为图3。Aa图3假设1:小孩B点所走曲线为沿着小棒a的方向(直线AB),则玩具A走的轨迹为直线(沿AB方向的)。此时,小孩行走的速度与玩具的速度相同。假设2:小孩B点所走曲线为一个A点为心的圆,则玩具不动。此时,如果小孩B行走的速度为v,而玩具A的速度却为零,这说明,在推玩具的过程中,小孩B的速度与玩具A的速度不同。由此特殊情况,我们可以看到,当小孩
小孩拉玩具问题.pdf
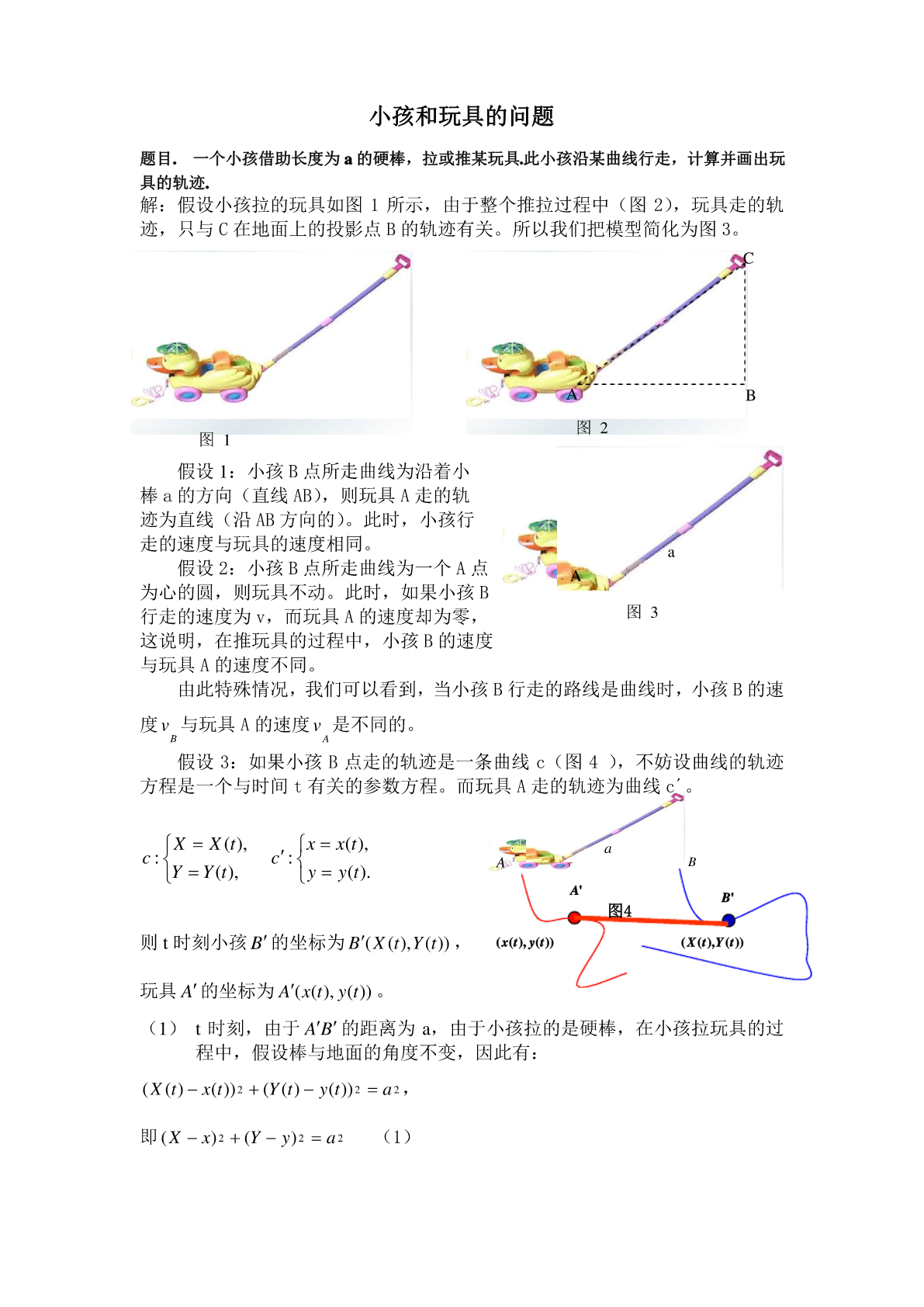
小孩和玩具的问题题目.一个小孩借助长度为a的硬棒,拉或推某玩具.此小孩沿某曲线行走,计算并画出玩具的轨迹.解:假设小孩拉的玩具如图1所示,由于整个推拉过程中(图2),玩具走的轨迹,只与C在地面上的投影点B的轨迹有关。所以我们把模型简化为图3。CAB图2图1假设1:小孩B点所走曲线为沿着小棒a的方向(直线AB),则玩具A走的轨迹为直线(沿AB方向的)。此时,小孩行走的速度与玩具的速度相同。a假设2:小孩B点所走曲线为一个A点A为心的圆,则玩具不动。此时,如果小孩B行走的速度为v,而玩具A的速度却为零,图3这

小孩拉玩具问题.docx
小孩和玩具的问题题目.一个小孩借助长度为a的硬棒,拉或推某玩具.此小孩沿某曲线行走,计算并画出玩具的轨迹.图1ABC图2解:假设小孩拉的玩具如图1所示,由于整个推拉过程中(图2),玩具走的轨迹,只与C在地面上的投影点B的轨迹有关。所以我们把模型简化为图3。Aa图3假设1:小孩B点所走曲线为沿着小棒a的方向(直线AB),则玩具A走的轨迹为直线(沿AB方向的)。此时,小孩行走的速度与玩具的速度相同。假设2:小孩B点所走曲线为一个A点为心的圆,则玩具不动。此时,如果小孩B行走的速度为v,而玩具A的速度却为零,这

数学建模-小孩拉玩具.doc
问题:一个小孩借助长度为a的硬棒,拉或推某玩具.此小孩沿某曲线行走,计算并画出玩具的轨迹.假设小孩沿的圆运动。小孩的坐标为,玩具的坐标为。如图:其中为玩具运动方向,为小孩运动方向。由题意知:(1)与之间的距离为硬棒的长度a。有①(2)玩具总在硬棒的方向上运动,因此,两个位置的差向量是玩具速度方向的倍数,即②(3)玩具的速度依赖于小孩的速度向量的方向,小孩的速度在硬棒上的投影是玩具的速度的模,③这里表示内积,为方向上的单位向量,则④⑤由①②③④⑤可得⑥因为我们假设小孩沿圆运动,由⑥可得:程序求解:建立M文件

(完整word版)数学建模-小孩拉玩具.doc
问题:一个小孩借助长度为a的硬棒,拉或推某玩具.此小孩沿某曲线行走,计算并画出玩具的轨迹.假设小孩沿的圆运动。小孩的坐标为,玩具的坐标为。如图:其中为玩具运动方向,为小孩运动方向。由题意知:(1)与之间的距离为硬棒的长度a。有①(2)玩具总在硬棒的方向上运动,因此,两个位置的差向量是玩具速度方向的倍数,即②(3)玩具的速度依赖于小孩的速度向量的方向,小孩的速度在硬棒上的投影是玩具的速度的模,③这里表示内积,为方向上的单位向量,则④⑤由①②③④⑤可得⑥因为我们假设小孩沿圆运动,由⑥可得:程序求解:建立M文件
