麻疯树施肥效果分析.pdf

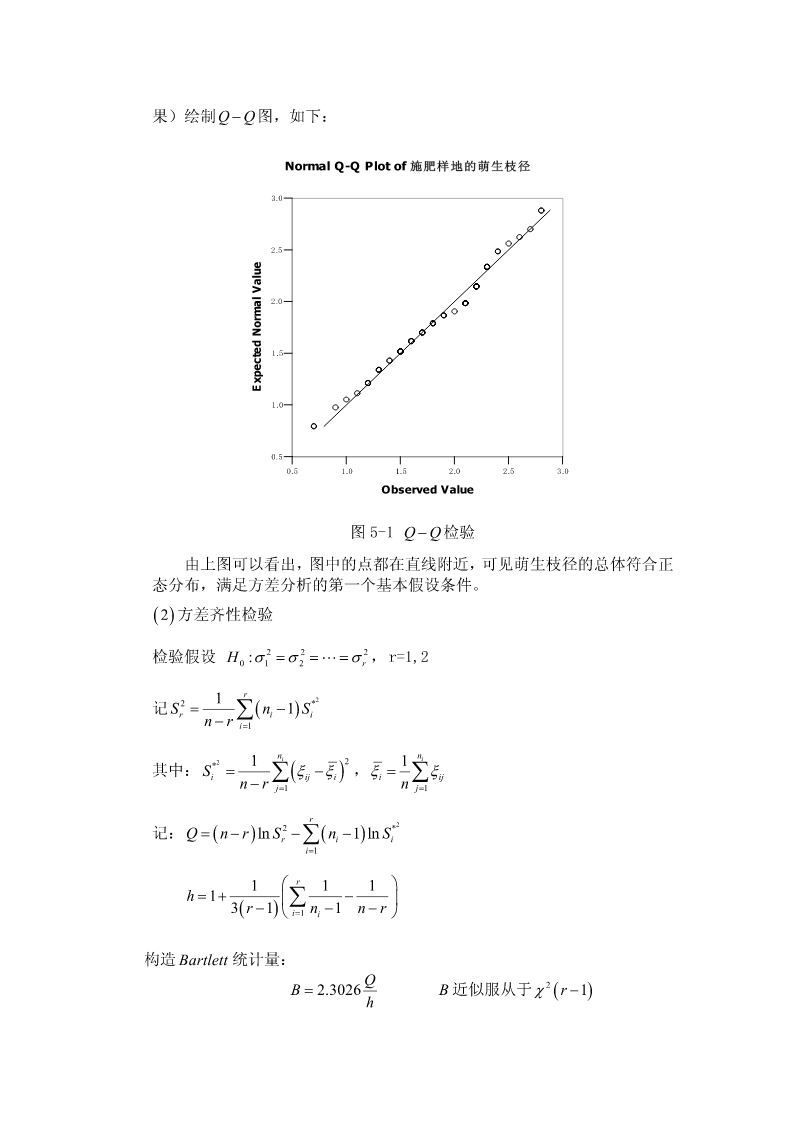
麻疯树施肥效果分析模型

1.问题重述
麻疯树被公认为是目前最具开发潜力的生物柴油树种，在西南地区具有资
源优势和发展潜力，目前，四川已成为了全国规模最大的麻疯树资源分布地区，
据最新调查统计，麻疯树资源发展面积达30万亩以上，主要集中在四川省的攀
西地区。但目前麻疯树生物柴油产业化发展仍存在一些技术关键问题---稳产、
高产问题。对麻疯树配方施肥试验的研究，是麻疯树果实（种子）产量高产、
稳产问题中一个重要的技术问题。
现以四川攀西地区的某地的硼肥喷施实验结果（见附表）为基础：
问题（1）：利用个体构件调查表的数据，通过对施肥样地和未施肥样地的
数据的对比分析，请你判断对样地的施肥的效果有无明显的改善。若有改善，
请给出施肥对枝长或者枝径增长值的定量数据结果。
问题（2）：在对开花座果情况进行调查数据时，明确知道已施肥和未施肥
的各有9株，另外两株（编号为11,22）由于实验人员的疏漏，不清楚是否施肥。
请对这两株未知样地判别其归属。
2.问题分析
2.1问题(1)的分析
该问题要求根据个体构件调查表的数据，对比分析施肥样地和未施肥样地的
数据，判断施肥效果是否明显，以及施肥对枝长或枝径增长值的定量数据结果。
首先，我们欲判断对样地的施肥效果是否明显，即需要判断分析施肥样地与未施
肥样地麻疯树的枝长、枝径、生殖次数等指标是否有显著性差别，对于研究一个
变量对多个因变量影响的一类问题，我们可以采用单因素方差分析的方法。
观察个体构件调查表的数据，不难发现，麻疯树枝的起源，即为萌发枝与否，
对植株的生殖次数有明显的影响，因此，首先需要将麻疯树枝根据起源进行分类，
分为萌发枝和非萌发枝。然后，可以利用SAS软件分别对于萌发枝和非萌发枝的
枝径、枝长和生殖次数进行单因素方差分析，根据P值和F值的结果来判定施肥
因素对三个指标的影响是否显著，从而判定对样地施肥的效果是否明显。在此基
础上，需要给出施肥对枝长或枝径增长量的定量描述，可以采用区间估计的方法，
以施肥与未施肥的枝长（或枝径）长度均值之差来表示增长值，从而给出95%置
信度下的区间估计。
2.2问题(2)的分析
在开花座果情况的调查表中，已知施肥和未施肥的麻疯树各有9株，由于第
5组之后的雄花和雌花的数据未加统计，并且鉴于雄花在授粉中与雌花的关系并
非对应，即各植株之间可以交叉授粉，而且在给定的数据中施肥样地和未施肥样
地的雌花的数量相差很小，通过SAS软件对雄花和雌花的方差分析，我们可以排
除雄花和雌花在判别植株施肥与否的作用，从而将这两个指标剔除。之后，可以
根据每株的头茬、二茬和三茬的结果数，结合方位，果实物候等变量，利用SPSS
进行判别分析，确定出相应的判别函数，再将未知样地两株的相应数据带入判别
函数，从而判定两植株的归属。
考虑到判别分析中,多个指标之间可能会有相关性的影响，一些特异性不强
的变量可能会干扰最终的判别结果，为了提高判别结果的正确率，我们将判别分
析法进行改进，采用逐步判别分析法，将判别性弱的因素剔除，使得分类函数中
的变量都是对判别结果的贡献最大的因素。借助于SPSS软件，通过逐步判别分
析得到相应的判别函数，重新进行判定，得到两株未知样地植株的归属。
3.模型假设
（1）假设所有试验植株的最初性状无差别；
（2）假设植株生长过程相互独立；
（3）忽略除施肥以外因素对两组植株生长造成的差异；
（3）假设个体构件表和开花座果表是无关联的；
（4）假设题目中所有数据正确可用。

4.符号说明

m表示所有数据的总均值；

mi表示施肥或未施肥组的均值；

ai表示施肥或未施肥组的均值与总体均值的差；
表示随机误差项，2；
xijxij:N(0,s)

yi(x)表示第i个线性判别函数；

x11表示未知样地植株11；

x22表示未知样地植株22；
其他符号在文中出现时给出具体说明
5.模型建立与求解

5.1问题(1)施肥效果的鉴定及定量描述
5.1.1施肥效果的鉴定
麻疯树枝的分类
根据个体构件调查表的数据，可以观察发现，起源为萌生枝的麻疯树枝的生
殖次数明显低于非萌生枝的，又根据生物学知识，侧枝萌生会抑制结果，即萌生
枝的生殖次数减少，因此我们将麻疯树枝按照萌生与否分为两类。
方差分析条件检验
由于该问题研究的是，施肥的效果对样地的植株的生长情况是否有明显改
善，属于一个因素对多个指标的影响问题，符合单因素方差分析的研究范围。因
为方差有相应的适用条件，即以下三个基本假设：
l在各个总体中因变量都服从正态分布；
l在各个总体中因变量的方差都相等；
l各个观测值之间是相互独立的。
为验证样地各指标的总体是否符合以上条件，需要做如下检验：
(1)正态性检验
本文利用SPSS（其他指标同理，限于篇幅，以下只给出萌生枝径的结
果）绘制Q-Q图，如下