
素材-全国-2019_五年级数学下册 一 分数的意义与性质 1《分数的意义》教材分析 浙教版.doc

甲申****66




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
素材-全国-2019_五年级数学下册 一 分数的意义与性质 1《分数的意义》教材分析 浙教版.doc
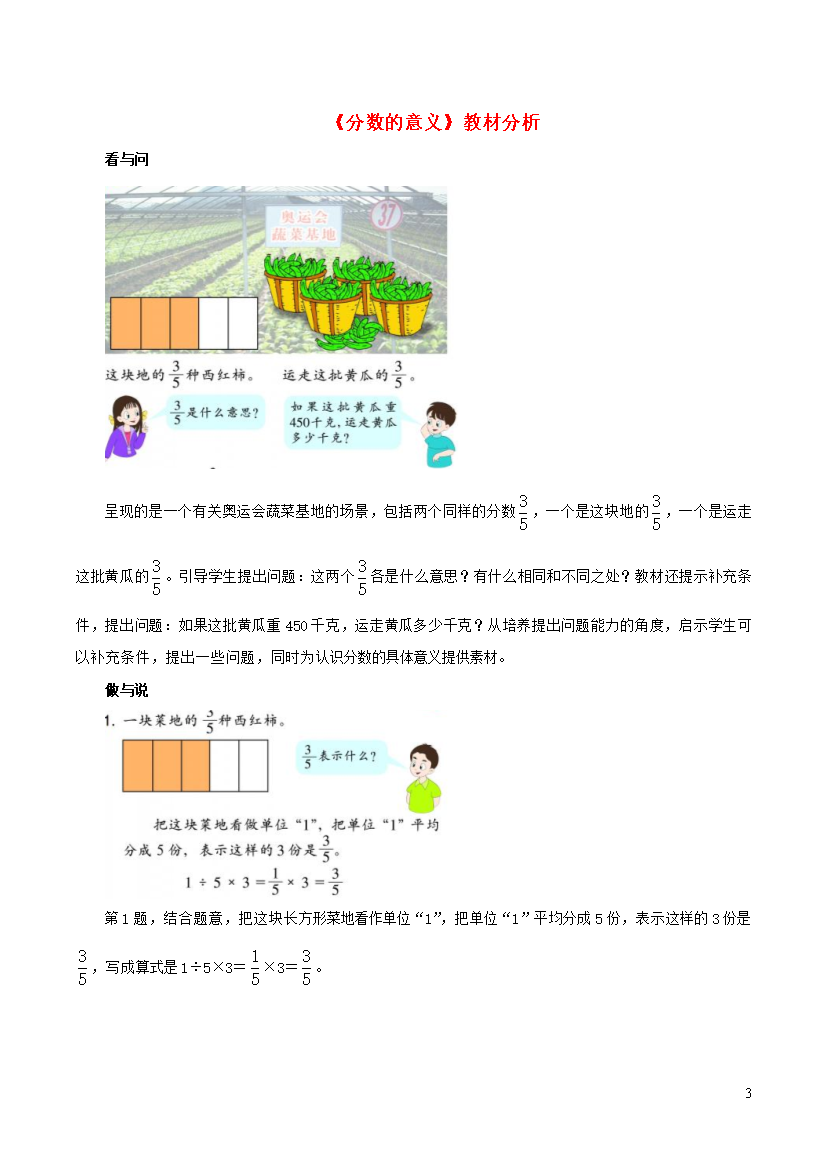
3《分数的意义》教材分析看与问呈现的是一个有关奥运会蔬菜基地的场景,包括两个同样的分数,一个是这块地的,一个是运走这批黄瓜的。引导学生提出问题:这两个各是什么意思?有什么相同和不同之处?教材还提示补充条件,提出问题:如果这批黄瓜重450千克,运走黄瓜多少千克?从培养提出问题能力的角度,启示学生可以补充条件,提出一些问题,同时为认识分数的具体意义提供素材。做与说第1题,结合题意,把这块长方形菜地看作单位“1”,把单位“1”平均分成5份,表示这样的3份是,写成算式是1÷5×3=×3=。

五年级数学下册 一 分数的意义与性质 1《分数的意义》教材分析 浙教版 素材.doc
《分数的意义》教材分析看与问呈现的是一个有关奥运会蔬菜基地的场景,包括两个同样的分数,一个是这块地的,一个是运走这批黄瓜的。引导学生提出问题:这两个各是什么意思?有什么相同和不同之处?教材还提示补充条件,提出问题:如果这批黄瓜重450千克,运走黄瓜多少千克?从培养提出问题能力的角度,启示学生可以补充条件,提出一些问题,同时为认识分数的具体意义提供素材。做与说第1题,结合题意,把这块长方形菜地看作单位“1”,把单位“1”平均分成5份,表示这样的3份是,写成算式是1÷5×3=×3=。第2题,针对单位“1”为具
素材-全国-2019_五年级数学下册 一 分数的意义与性质 3《分数的基本性质》教材分析 浙教版.doc
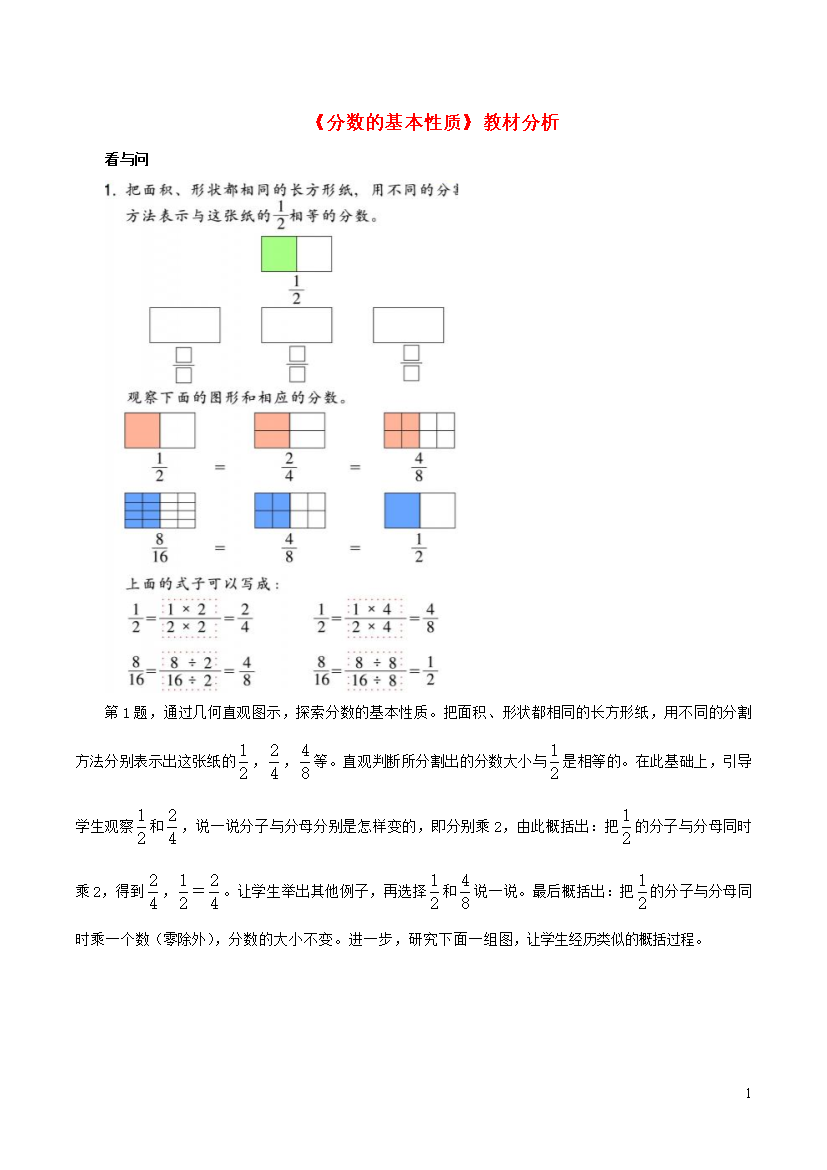
1《分数的基本性质》教材分析看与问第1题,通过几何直观图示,探索分数的基本性质。把面积、形状都相同的长方形纸,用不同的分割方法分别表示出这张纸的,,等。直观判断所分割出的分数大小与是相等的。在此基础上,引导学生观察和,说一说分子与分母分别是怎样变的,即分别乘2,由此概括出:把的分子与分母同时乘2,得到,=。让学生举出其他例子,再选择和说一说。最后概括出:把的分子与分母同时乘一个数(零除外),分数的大小不变。进一步,研究下面一组图,让学生经历类似的概括过程。第2题,先引导学生观察,这些
素材-全国-2019_五年级数学下册 一 分数的意义与性质 2《分数的大小比较(一)》教材分析 浙教版.doc
3《分数的大小比较(一)》教材分析本课主要学习同分母或同分子的分数大小比较,侧重于通过直观图示与意义理解,让学生概括出比较的方法。看与问教师先提供一些分数,也可以让学生说出一些分数,再选择两个比较它们的大小。把学生选择的情况分成三类,一类是同分母的,一类是同分子的,还有一类是分子、分母各不相同的,并指明,今天主要研究前面两类。做与说第1题,同分母分数的大小比较。(1)主要借助于直观图示,先说明用一个长方形直条单位“1”分别表示与,在图中指出分数表示的大小,再说出两个分数的大小关

素材-全国-2019_五年级数学下册 一 分数的意义与性质 8《分数与小数的互化》教材分析 浙教版.doc
1《分数与小数的互化》教材分析做与说创设了一个比较巧克力质量大小的情境,引发学生比较小数和分数大小的现实需求,把“哪一盒巧克力较重”这个生活问题转化成“比较两个数大小”的数学问题。第1题,怎样比较0.4与的大小?组织学生独立思考,尝试比较。在自主思考的基础上组织讨论:一种方法是把小数转化成分数,然后比较两个分数的大小;另一种方法是把分数化成小数,再比较两个小数的大小。第2题,根据已有的知识经验,一位小数就是分母是10的分数,两位小数就是分母是100的分数……在此基础上总结方法:
