
69-某船用带阻尼板齿轮振动分析.pdf

as****16




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

69-某船用带阻尼板齿轮振动分析.pdf
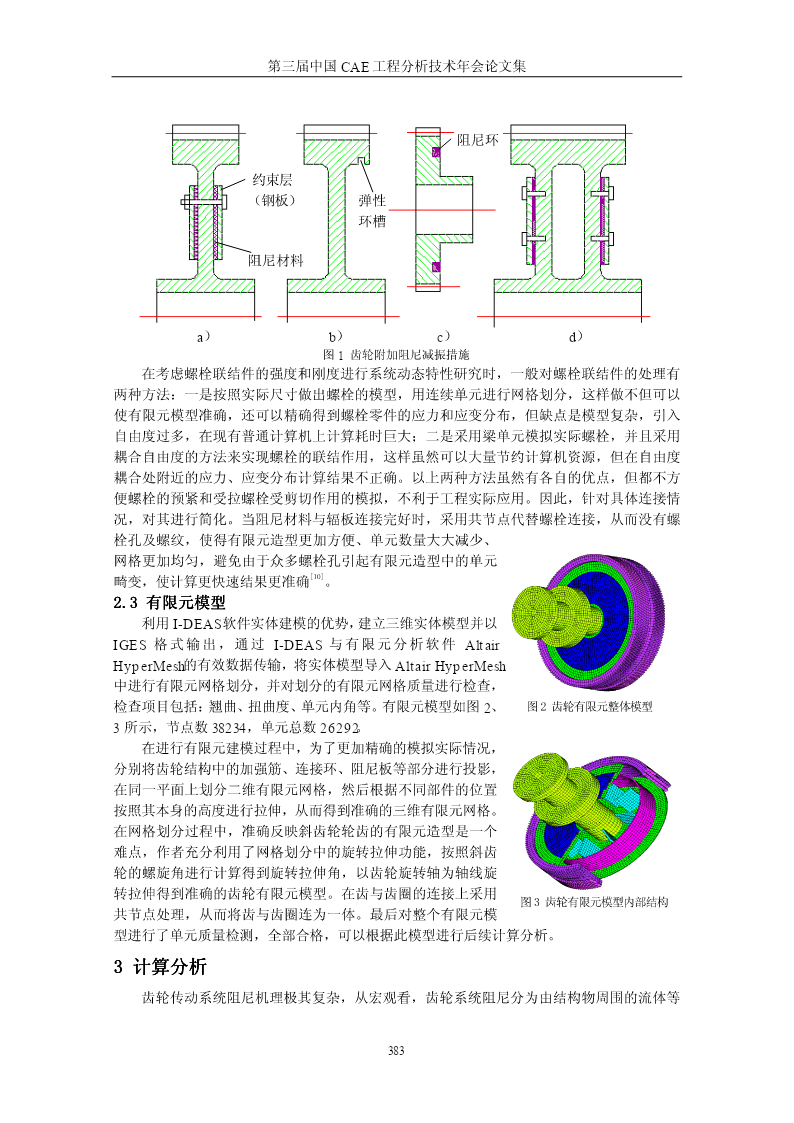
第三届中国CAE工程分析技术年会论文集某船用带阻尼板齿轮振动分析陈艳锋吴新跃谢最伟(海军工程大学船舶与动力学院,湖北武汉430033)摘要:::齿轮传动:振动噪声往往是采用齿轮传动机器的主要噪声源,是评价产品质量优劣的一项重要指标。因此,如何减小齿轮传动振动噪声已成为当今世界一个重要研究课题。采用齿轮外加阻尼层的方法降低齿轮传动系统振动噪声有着广泛的应用前景。某船用齿轮传动装置中采用在齿轮辐板上添加阻尼的措施达到减振的目的,对此种结构的固有特性进行了计算分析,并对下一步研究工作进行了简略介绍。关键词:::

某型船用传动齿轮箱振动模态的试验与分析.doc
作者:海军工程大学王基吴新跃朱石坚摘要:某多输入双级传动齿轮箱是舰船振动与噪声的主要根源之一。文中在建立齿轮箱的试验模型后,采用固定锤击点改变测量点法采集各点的冲击数据和响应数据,在对同类型两部齿轮箱的模态试验的结果分析的基础上,通过对比找到了其中一部齿轮箱振动噪声增大的原因,经过对该齿轮箱的开箱测检结果表明,其分析结论是正确的。对该型舰船齿轮箱的故障诊断、提高其可靠性和维修性,具有重要的指导意义。关键词:齿轮箱;振动;噪声;模态试验舰船齿轮箱不仅要求传递功率大、体积小、重量轻,还要求其振动小、噪声低[1

某船用齿轮断裂分析.docx
某船用齿轮断裂分析船用齿轮断裂分析摘要船用齿轮在航海运输中承担着重要的传动任务,然而由于工况的复杂性和操作环境的恶劣特点,船用齿轮断裂问题一直备受关注。本论文通过对船用齿轮的断裂进行分析,并结合实际案例,探讨了齿轮断裂的原因、影响因素和预防措施,旨在提供一定的参考和借鉴。1.引言船用齿轮断裂问题不仅会带来巨大的经济损失,还会危及人员的生命和财产安全。因此,对于船用齿轮的断裂问题进行深入研究,分析其原因并提出相应的预防措施具有重要的现实意义。2.船用齿轮断裂原因分析2.1材料本身缺陷船用齿轮制造过程中,可能

船用齿轮箱扭转振动分析.docx
船用齿轮箱扭转振动分析船用齿轮箱扭转振动分析摘要:船用齿轮箱作为重要的传动装置,在船舶运行过程中承受着复杂的载荷。由于其特殊的工作环境和作业要求,齿轮箱扭转振动问题是船舶运行过程中一个重要的研究课题。本文将对船用齿轮箱的扭转振动进行分析,并探讨其对船舶整体性能的影响。导言:船用齿轮箱的扭转振动是指在船舶运行过程中齿轮箱对扭矩的反应造成的振动现象。船舶运行过程中,船体和发动机等组件会对齿轮箱施加扭矩载荷,当扭矩载荷超过齿轮箱的承载能力时,就会导致齿轮箱产生振动。齿轮箱的扭转振动主要有两种形式:自由振动和强迫

某船用主机中间支架振动特性分析.docx
某船用主机中间支架振动特性分析某船用主机中间支架振动特性分析摘要:船用主机中间支架的振动特性对船舶的正常运行和航行的安全性至关重要。本论文通过理论分析和实验测试的方式,对船用主机中间支架的振动特性进行了深入研究。首先,我们介绍了船用主机中间支架的工作原理和结构组成;其次,通过模拟分析和试验验证,得到了中间支架的振动特性数据;最后,我们根据分析结果提出了相应的优化措施,以提高船用主机中间支架的工作效率和减小振动噪音。关键词:船用主机、中间支架、振动特性、优化措施第一节引言船用主机是船舶上重要的设备之一,主要
