
线性回归分析的SPSS操作(多元线性回归).pdf

qw****27






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

线性回归分析的SPSS操作(多元线性回归).pdf
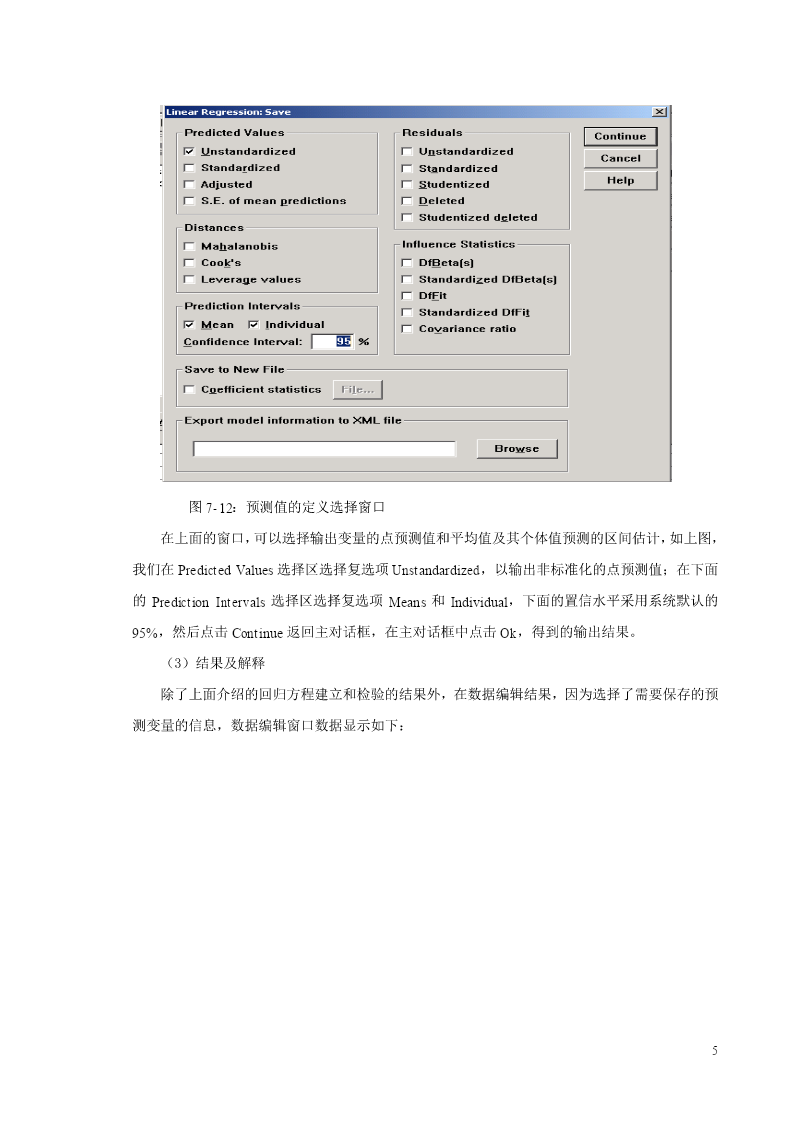
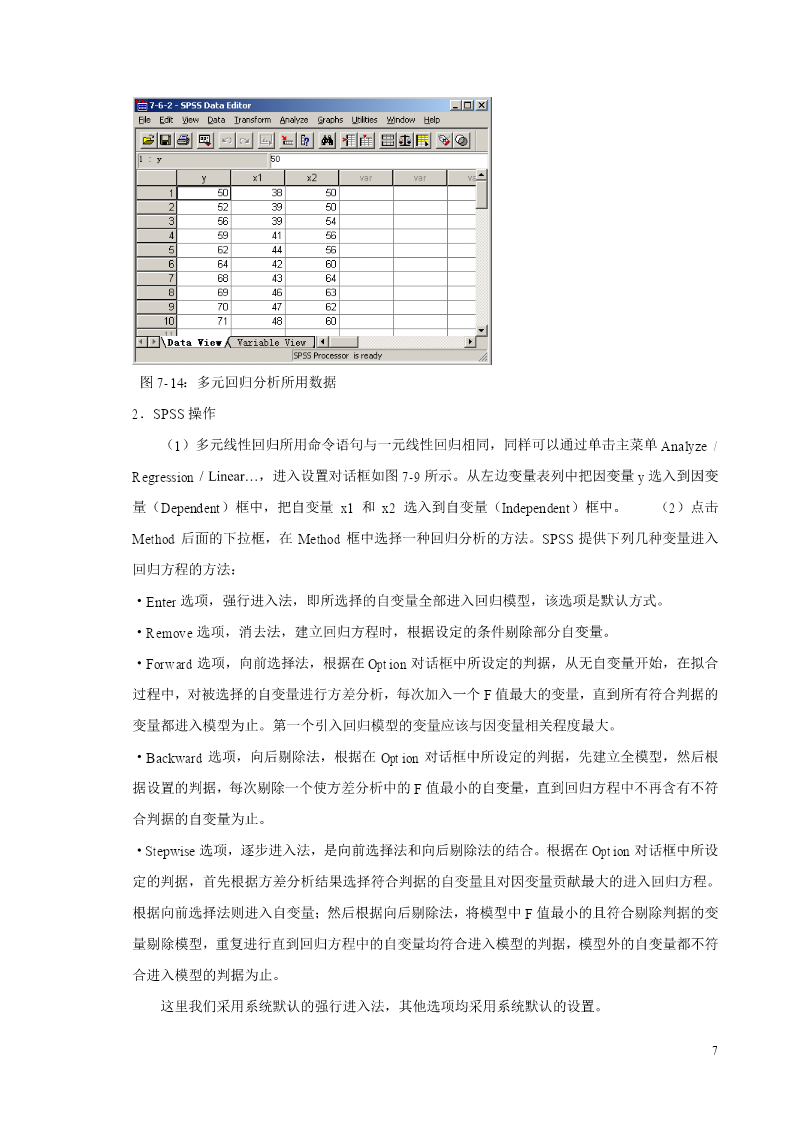
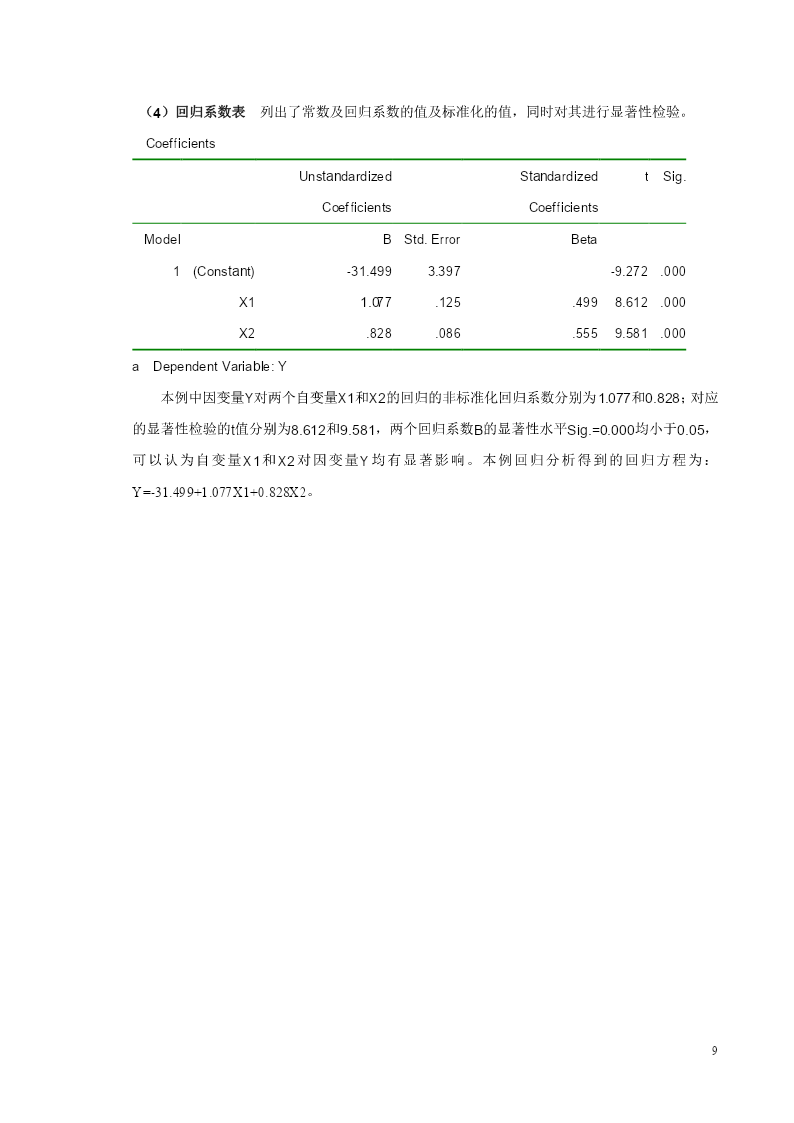
线性回归分析的SPSS操作本节内容主要介绍如何确定并建立线性回归方程。包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。为了确保所建立的回归方程符合线性标准,在进行回归分析之前,我们往往需要对因变量与自变量进行线性检验。也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验,这里不再重复。另外,通过散点图还可以发现数据中的奇异值,对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。一、一元线性回归分析1.数据以本章第三节例3的数据为例,简单介绍利用SPSS如何进
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归.pdf
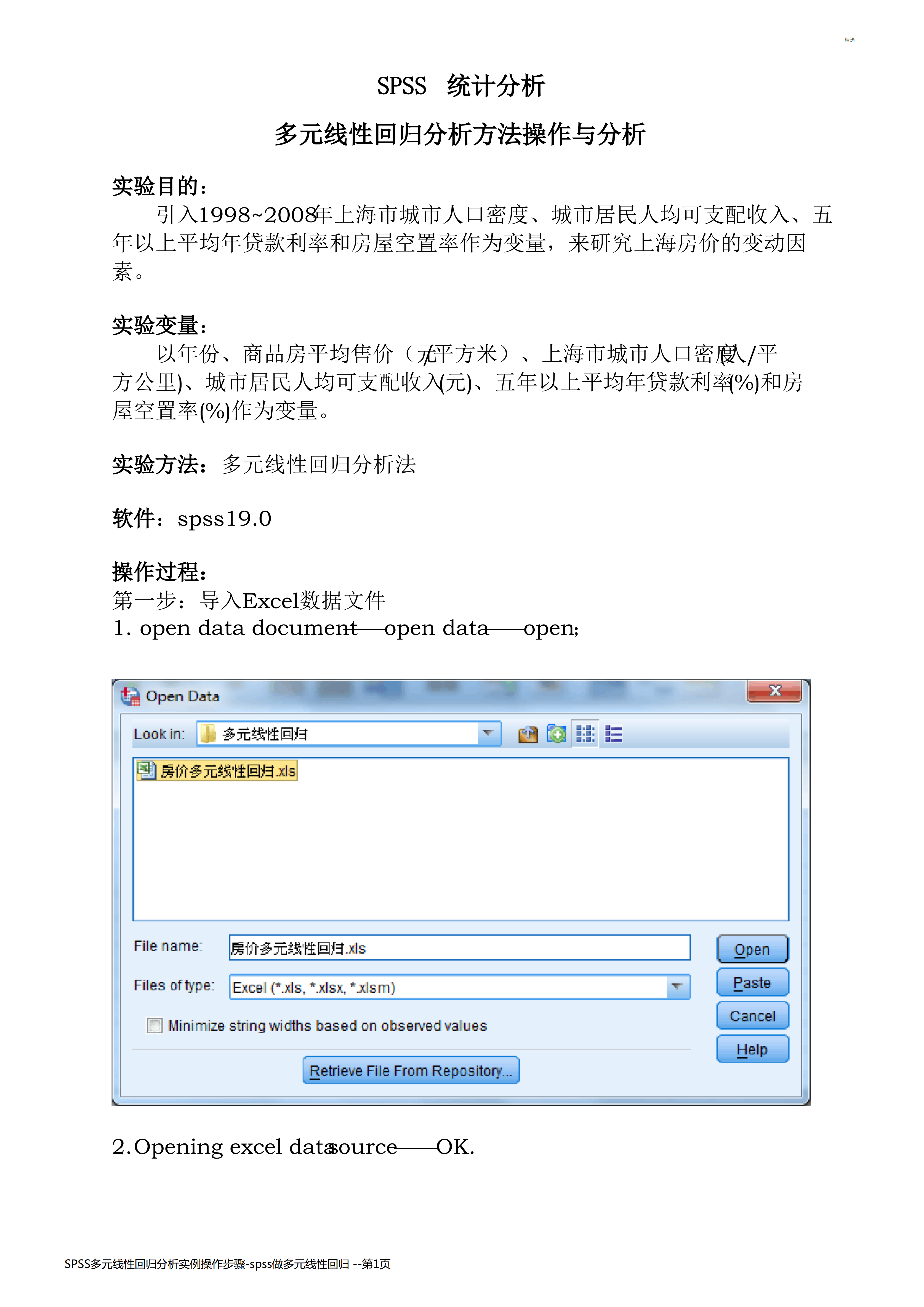
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归--精选SPSS统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Exc
SPSS多元线性回归分析实例操作步骤-spss做多元线性回归.pdf
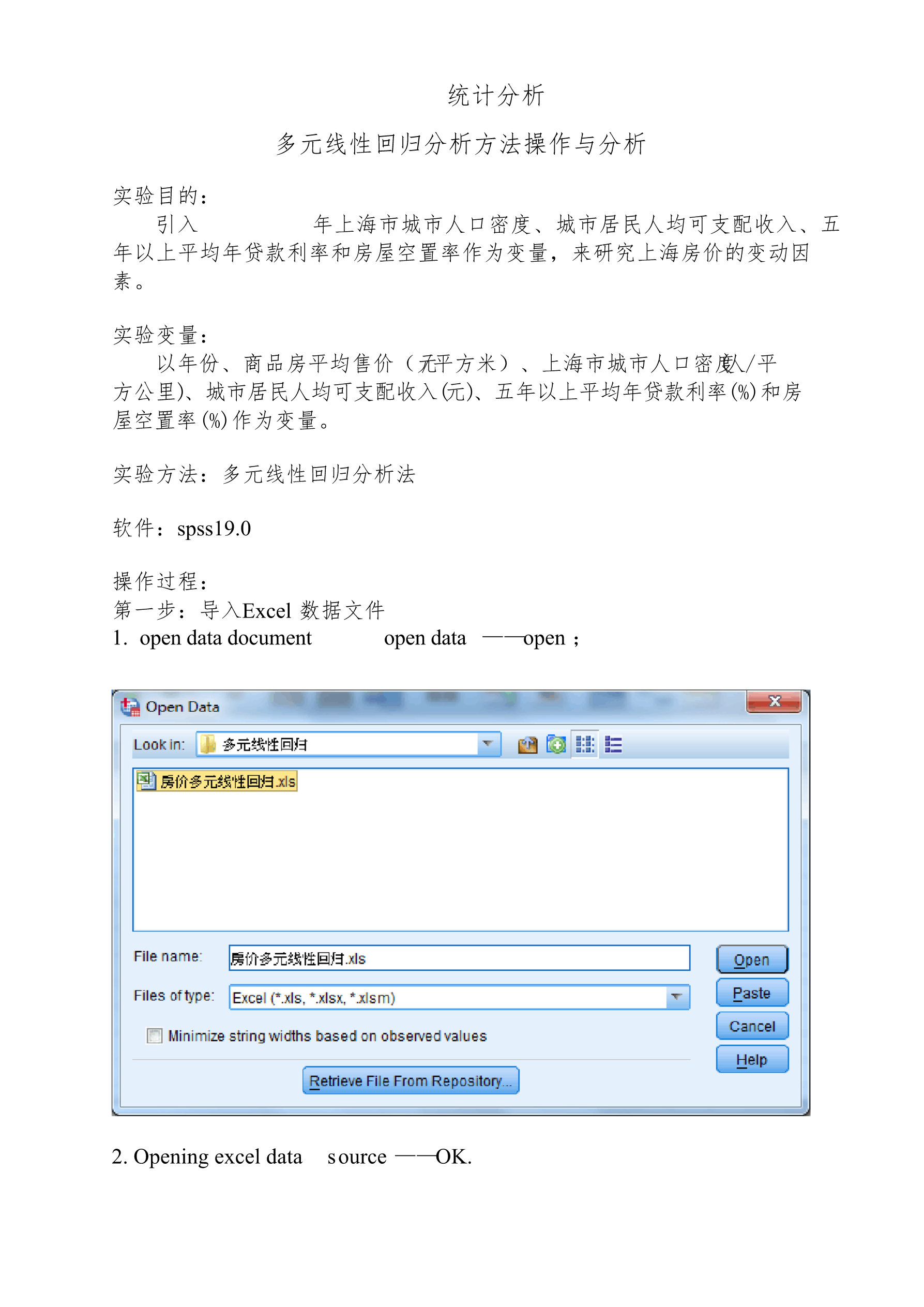
统计分析多元线性回归分析方法操作与分析实验目的:引入年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.opendatadocumentopendata——open;2.Openin

spss多元线性回归分析.doc
spss多元线性回归分析SPSS多元线性回归分析试验在科学研究中,我们会发现某些指标通常受到多个因素的影响,如血压值除了受年龄影响之外,还受到性别、体重、饮食习惯、吸烟情况等因素的影响,用方程定量描述一个因变量y与多个自变量x1、x2、x3.......之间的线性依存关系,称为多元线性回归。有学者认为血清中低密度脂蛋白增高是引起动脉硬化的一个重要原因。现测量30名怀疑患有动脉硬化的就诊患者的载脂蛋白A、载脂蛋白B、载脂蛋白E、载脂蛋白C、低密度脂蛋白中的胆固醇含量。资料如下表所示。求低密度脂蛋白中的胆固醇

spss多元线性回归分析.docx
SPSS多元线性回归分析试验在科学研究中,我们会发现某些指标通常受到多个因素的影响,如血压值除了受年龄影响之外,还受到性别、体重、饮食习惯、吸烟情况等因素的影响,用方程定量描述一个因变量y与多个自变量x1、x2、x3.......之间的线性依存关系,称为多元线性回归。有学者认为血清中低密度脂蛋白增高是引起动脉硬化的一个重要原因。现测量30名怀疑患有动脉硬化的就诊患者的载脂蛋白A、载脂蛋白B、载脂蛋白E、载脂蛋白C、低密度脂蛋白中的胆固醇含量。资料如下表所示。求低密度脂蛋白中的胆固醇含量对载脂蛋白A、载脂蛋
