基于GARCH_VaR模型的ETF基金市场风险的实证分析.pdf

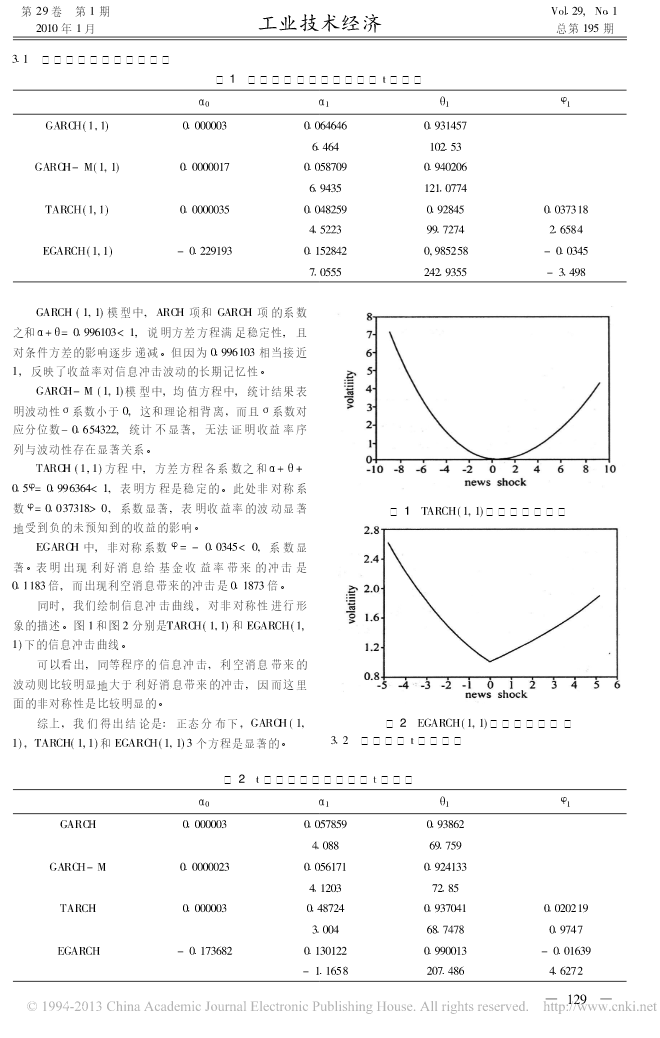
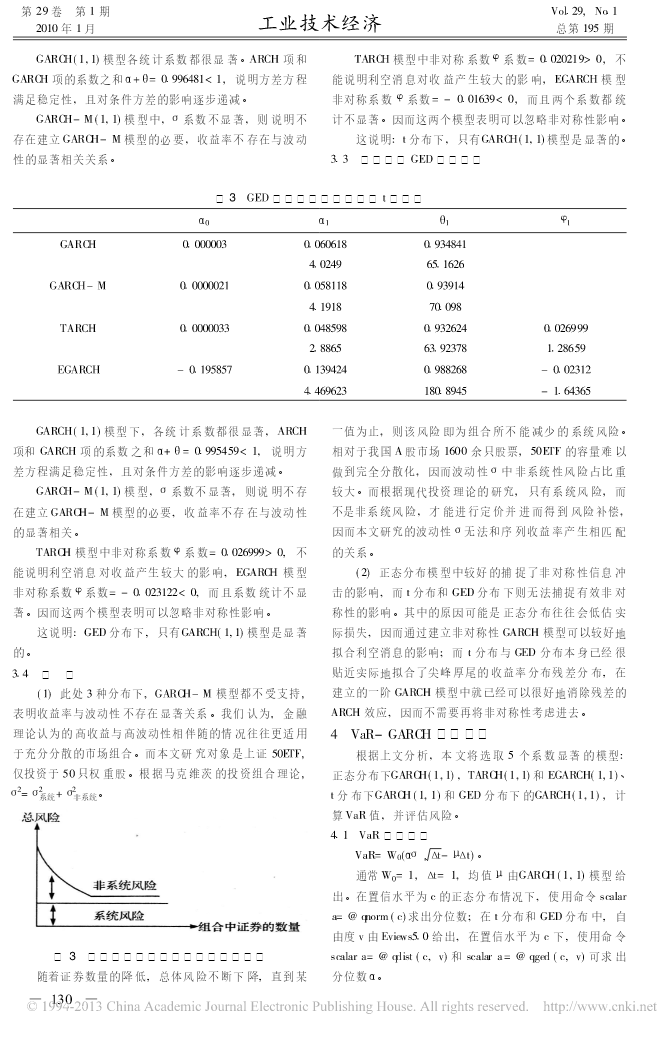
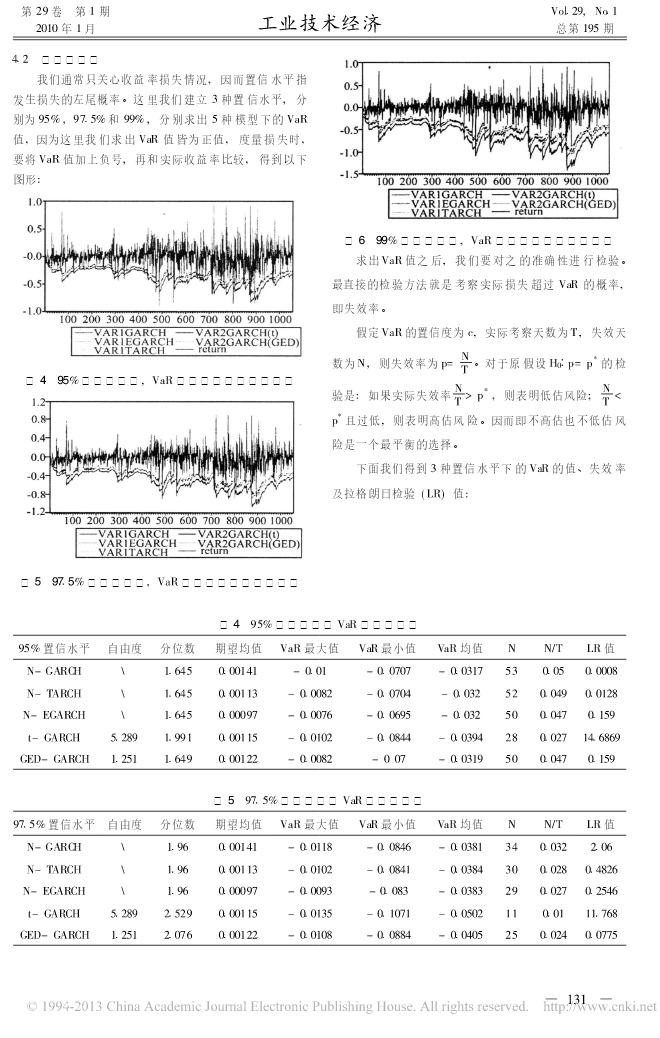
第29卷第1期Vol129,No11
2010年1月工业技术经济总第195期

基于GARCH-VaR模型的ETF
基金市场风险的实证分析

周昭雄1王剑2
1(上海理工大学,上海200000)2(上海东华大学,上海200051)

1摘要2ETF基金是我国少有的金融创新产品之一,然而在近年来急涨骤跌的股市中,ETF面
临着很大的市场风险,但国内尚缺乏关于ETF基金市场风险的定性研究。同时在此次全球金融危机中,
如何加强金融工具的风险管理已成为当务之急。因此,本文以我国上市最早的50ETF为研究对象,在正
态分布、t分布与GED分布3种情况下,建立了GARCH族模型计算动态方差,研究了ETF基金的收益
风险补偿问题与非对称信息冲击问题,接着用方差)))协方差方法求出VaR值,在3种置信水平下通过
与实际收益率的比较来度量市场风险,然后对VaR值的准确性进行检验,最后分析得出最适合估计ETF
市场风险的模型。
1关键词2ETFGARCH风险动态方差
1中图分类号2F8301911文献标识码2A

ETF(Exchangetradedfund,交易所交易基金)是全Prob($P>VaR)=1-c
球金融市场在90年代以来的最成功的金融创新产品之其中,$P表示资产在持有期t内的损失,c是给定
一。ETF是以复制和追踪某一市场指数为目的,通过充的置信水平。现实中我们常用的公式为:
*
分分散化的投资策略,降低非系统风险和通过被动的投VaR=-W0R=W0(AR$t-L$t)
资管理方式最大限度地降低交易成本从而取得市场
,,W0是初始投资额,R为投资收益率,预期均值和波
平均收益。2005年,我国首只ETF基金上市,迄今,我
动率分别为L和R。本文将选取方差)))协方差法计算
国共有5只ETF基金。而在几年来股市牛熊转换的涨落
VaR值。
中,ETF基金的市场风险不断放大,同时,在金融性金
112GARCH族模型
融危机的大背景下,怎样加强对基金的风险管理已成为
现实中的金融时间序列存在严重的波动集聚性,即
基金管理者的一个重要课题。VaR方法能以一个风险值
大幅波动往往集中在某一时段,小幅波动往往集中在另
表示各类风险并给出风险的发生概率,因而成为当前风
一时段,则收益率的方差R不稳定。因此,我们需要引
险管理界最广为应用的方法。GARCH族模型可以有效地
入能有效估计时变方差的GARCH族模型对VaR进行动
描述金融时间序列的尖峰厚尾的特征,追踪收益率的动
态估计。
态方差进而可以精确地计算VaR值,因而得到研究人员
(1)GARCH模型:Bollerslev1T(1986)提出了广义
的重视。因此,本文将以50ETF为样本,从收益的波动
自回归条件异方差模型GARCH模型(generalizedautore-
性与概率分布出发,建立GARCH族模型,计算VaR值,
gressiveconditionalheteroskedasticitymodel),表达式如下:
分析VaR值与实际收益率的差别,通过综合比较得出最
合适的模型,为基金管理者评估、度量与防范风险提供yt=xctB+Et
qp
决策的参考。2
ht=A0+EAiEt-i+EHjht-j
1模型建立i=1j=1
其中,h=R2,pE0,q>0;A>0,AE0,i=1,,
111VaR介绍tt0i
2
1993年7月,G30集团在研究金融衍生品种的基础q;HjE0,j=1,,,p,EtùN(0,Rt)。
上,提出了度量市场风险的VaR(ValueatRisk)方法,(2)基于收益风险补偿的GARCH-M模型:金融理
并首次对VaR进行了较为详细的介绍。VaR是当前最主论表明收益应当与其风险成正比,较高的风险的资产可
流的风险度量方法。菲利普#乔瑞(Philippe#Jorion)给出以获得更高的平均收益。这种利用条件方差表示预期风
的权威的定义是,VaR是在一定的置信水平下和一定的险的模型被称为GARCH-M模型(GARCH-in-mean),
目标期间内,预期的最大损失。数学公式表示为:模型表达式为:

收稿日期:2009)09)15

)127)
第29卷第1期Vol129,No11
2010年1月工业技术经济总第195期

2
yt=xctB+Et+KRt广泛的是t分布及GED分布。本文假定收益率残差序列
222分别服从正态分布、分布及分布来对模型参数
Rt=R0+R1Et-1+,+RqEt-qtGED,
2进行估计。
其中,参数K是用条件方差Rt衡量的,可观测到的

预期风险波动对yt的影响程度,代表了风险与收益的一2数据检验
种平衡。本文样本区间是2005年2月23日到2009年6月19
(3)基于非对称性的TARCH模型:基于股票市场的日,共计1056组数