
广义逆矩阵及其应用.ppt

yy****24






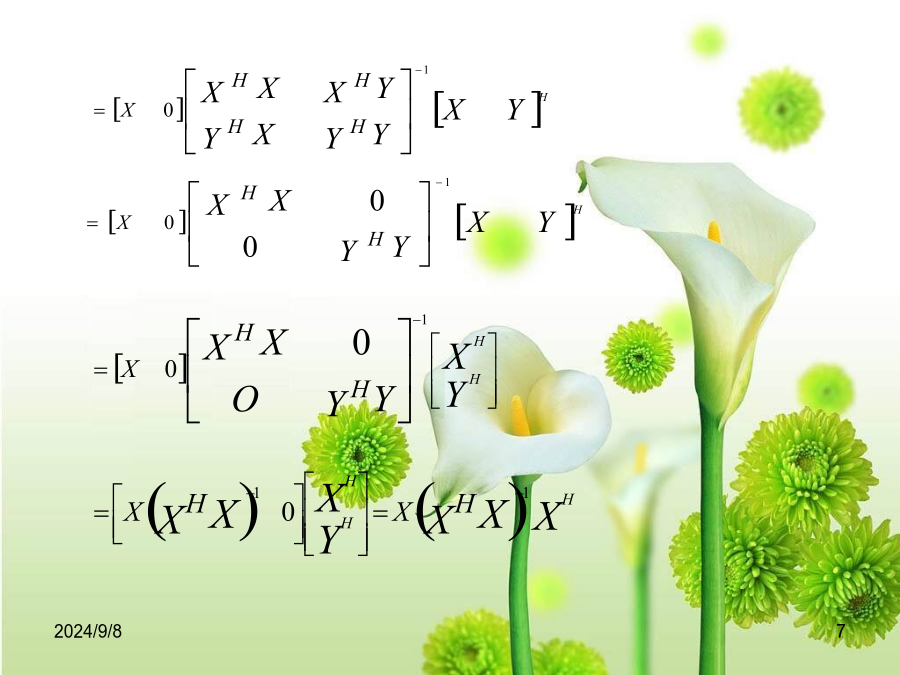



亲,该文档总共38页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

广义逆矩阵及其应用.docx
广义逆矩阵及其应用一、引言在理论研究和实际应用中,矩阵是一种非常重要的数学工具。在矩阵运算中,逆矩阵扮演着非常重要的角色。矩阵的逆定义为:对于一个n阶矩阵A,若满足AA^{-1}=A^{-1}A=E,则矩阵A的逆矩阵存在,称A为可逆矩阵,A^{-1}为A的逆矩阵。但是,在实际应用中,矩阵可能不一定是可逆的,此时就需要用到广义逆矩阵。二、广义逆矩阵的定义和性质广义逆矩阵的定义:对于一个m×n的矩阵A,若矩阵X满足AXA=A①且XAX=X②,则称矩阵X是A的广义逆矩阵,记作A^+。下面是广义逆矩阵的几个基本性

广义逆矩阵及其应用.ppt
广义逆矩阵及其应用广义逆矩阵及其应用广义逆矩阵的定义2,1920年Moore广义逆定义定义3:设W是数域P上n维线性空间V的一个m维子空间为可逆方阵另外2024/9/8(3),Moore广义逆定义广义逆矩阵的求法一、减号逆引理:设Bm×n=Pm×mAm×nQn×n其中PQ可逆,则A-=QB-P,B-=Q-A-P-由引理可知求得Q,B-,P即可得到A的一个特定减号逆解:先对A进行行变换10-1110010-111000222010011101/20-145300100001/4-1/21/4证明:验证AXA

广义逆矩阵的性质及应用.docx
广义逆矩阵的性质及应用广义逆矩阵的性质及应用一、引言广义逆矩阵是线性代数中的一个重要概念,广义逆矩阵是对于非方阵而言的一种逆矩阵的概念。在实际应用中,广义逆矩阵具有广泛的应用领域,在数据处理、最小二乘法、线性回归等问题中发挥着重要的作用。本文将以广义逆矩阵的性质和应用为主题,探讨广义逆矩阵的定义、性质及其在实际问题中的应用。二、广义逆矩阵的定义设A是一个m×n的矩阵,称矩阵X是A的广义逆矩阵,如果满足下列条件:1.AXA=A;2.XAX=X;3.(AX)’=AX;4.(XA)’=XA。其中,(·)’表示矩

广义逆矩阵计算及在矩阵方程中应用的研究.docx
广义逆矩阵计算及在矩阵方程中应用的研究一、概述广义逆矩阵是矩阵理论中的重要概念,它在数学、物理、工程、计算机科学等多个领域都有着广泛的应用。与传统的逆矩阵相比,广义逆矩阵具有更广泛的定义和更灵活的性质,使得它在处理一些复杂问题时具有独特的优势。在计算方面,广义逆矩阵的求解方法多种多样,包括直接法、迭代法、分块法等。这些方法各有特点,适用于不同规模和特性的矩阵。随着计算机技术的不断发展,广义逆矩阵的计算效率也得到了显著提升,使得大规模矩阵的广义逆计算成为可能。在矩阵方程中的应用方面,广义逆矩阵为求解各类矩阵

矩阵的广义逆.ppt
矩阵的广义逆矩阵的广义逆§4.1矩阵的左逆与右逆2、左逆和右逆存在的条件的存在性矩阵右逆的存在性定理4.2(P.94)ACmn,则下列条件等价:矩阵A右可逆。A的列空间R(A)=Cmnm,秩(A)=m,A是行满秩的。矩阵AAH可逆=AH(AAH)–1二、单侧逆和求解线性方程组AX=b二、单侧逆和求解线性方程组AX=b§4.2广义逆矩阵二、Moore-Penrose(M-P)广义逆3、M-P广义逆的存在性及其求法定理4.8(P.99)任何矩阵都有M-P广义逆。求法:设A满秩分解A=BC,则A+=CH(
