有限元计算细观力学对复合材料力学行为的数值分析.pdf

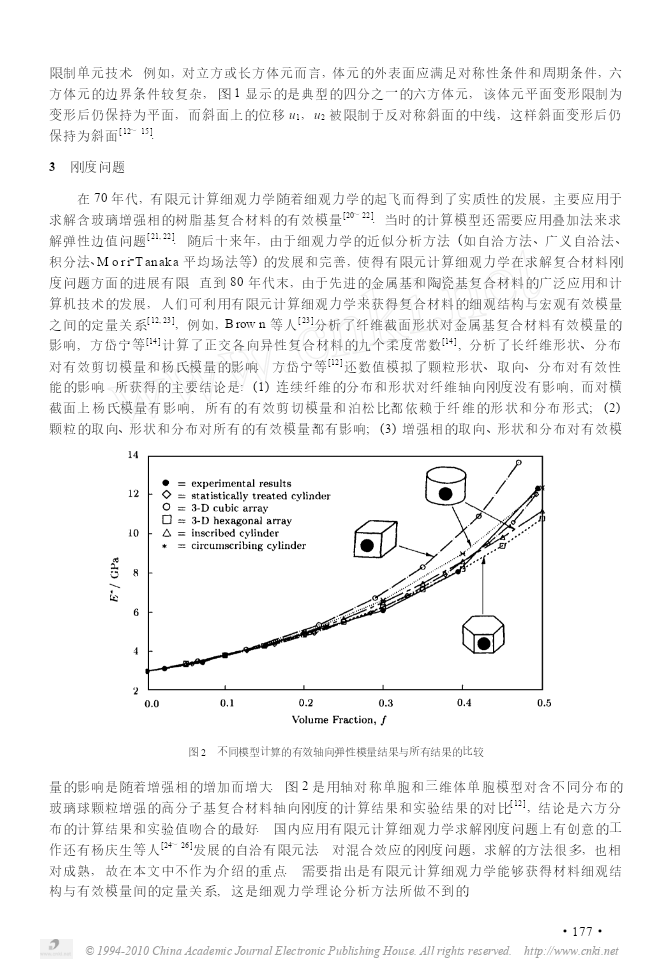
第28卷第2期力学进展Vol128No12
1998年5月25日ADVANCESINMECHANICSMay25,1998

有限元计算细观力学对复合材料力
学行为的数值分析3

方岱宁周储伟

清华大学工程力学系北京100084

摘要有限元计算细观力学的发展是近十年来细观计算力学发展的主要特征和推动力.本文综
述了有限元计算细观力学近十年来应用于复合材料力学行为分析研究方面的进展.介绍了基本的数
值模型和计算方法,重点评述了强度和损伤等协同效应问题上的最新研究成果.最后对有限元计算
细观力学应用于材料设计的前景做了展望.

关键词细观力学,有限元,复合材料,刚度,强度,损伤,任意分布,材料设计

1引言

复合材料的就位特性、各向异性和呈层性所产生的各种复杂的力学现象,使得有限元计算
技术对于求解复合材料及其结构的力学问题得到了相当广泛的应用[1,2].在这一领域可分为两个
分支:一是有限元法应用于复合材料结构(如板、壳等)力学问题[1];二是有限元技术应用于复
合材料细观力学行为的模拟分析[3,4].前者追求真实工程环境下的工程结构问题的解决,后者侧
重于材料细观结构与力学性能的关系分析.有限元法与细观力学和材料科学相结合产生了有限
元计算细观力学[3,4].作为细观计算力学[5]的最主要的组成部分,有限元计算细观力学的发展一
直是近十年来细观计算力学发展的主要特征和推动力.它主要研究组分材料间力的相互作用和
定量描述细观结构与性能间的关系.由于复合材料综合了不同单相材料的长处,对其材料力学
行为的有意义的研究必须借助于细观力学进行.界面行为,损伤和动态行为对复合材料尤为重
要.因此,有限元计算细观力学在求解复合材料细观力学问题中的应用正是在70年代随着细观
力学的起飞而发展起来的[5～7].但是,该领域却是在80年代末随着计算材料科学(Computational
materialsScience)[8,9]或称计算机辅导材料设计(Computer-AidedMaterialsDesign)兴起而真
正得到迅猛发展.这主要由于下述因素促成的:(1)细观力学理论解析的方法,至今还主要限于
解决复合材料有效刚度混合效应的问题,尚不能解决与复杂损伤强度相关的协同效应、非比例
加载响应和其有尖棱角(非旋转体)增强相的细观结构等问题[3,10];(2)复合材料在力学加载下
的细观结构信息不可能在实验中以系统的方法获得[3,10];(3)超级计算机的发展和有限元计算

3国家自然科学基金资助项目
收稿日期:1996207213,修回日期:1997211221

·173·
©1994-2010ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net
软件的商业化,基本克服了有限元细观计算力学的最大缺点--输入数据工作量大和花费比较
长的计算机时;(4)最重要的还是在于有限元细观计算力学方法能够描述复合材料的细观结构
对宏观响应的影响的关系,使得特别设计的细观结构对载荷是如何响应和如何失效的问题可以
进行数值模拟[3].有限元细观计算力学的最大优点在于它能够获得纤维(或颗粒)直径尺度下的
完整的应力2应变场来反映复合材料宏观应力-应变响应特征.这样,它能够分析宏观有效性能
对细观结构的依赖关系.例如:能定量描述诸如纤维(或颗粒)的形状、尺寸、分布和体积含
量等这些细观结构参量对宏观力学性能的影响.而这些优点正是计算材料科学在材料细观结构
设计时所必需的[11].在复合材料结构设计中,可以控制界面条件,纤维-基体的排列方式,颗
粒(纤维)的形状和尺寸,这样就可能修改其强度和其他有关的力学性质,满足指定的功能要
求.这种在计算机指导下设计具有特殊性能的复合材料细观结构的要求给有限元计算细观力学
发展提供了机会和挑战.
本文首先介绍了主要的材料模型和基本的计算方法,重点评述了有限元计算细观力学对复
合材料力学行为中较为困难的塑性流动、强度及损伤协同效应问题和增强相任意分布问题数值
模拟求解方面的进展,讨论了复合材料细观结构对宏观性能的影响,最后对有限元计算细观力
学应用于材料设计做了展望.

2材料模型和计算方法

211材料模型
有限元细观计算力学应用于复合材料力学行为数值模拟的本质,是将有限元计算技术与细
观力学和材料学相结合,根据复合材料具体细观结构,建立代表性细观计算体元、界面条件和
边界条件,求解受载下体元中具有夹杂的边值问题.从而建立起细观局部场量与宏观平均场量
间的关系,最终获得复合材料的宏观力学响应.虽然现代计算技术能容易地获得全场解,但在
有限元计算细观力学中,大多数数值解是应用了较理想的增强相周期分布的材料模