
复合材料网格加筋结构的阻尼特性研究.pdf

as****16




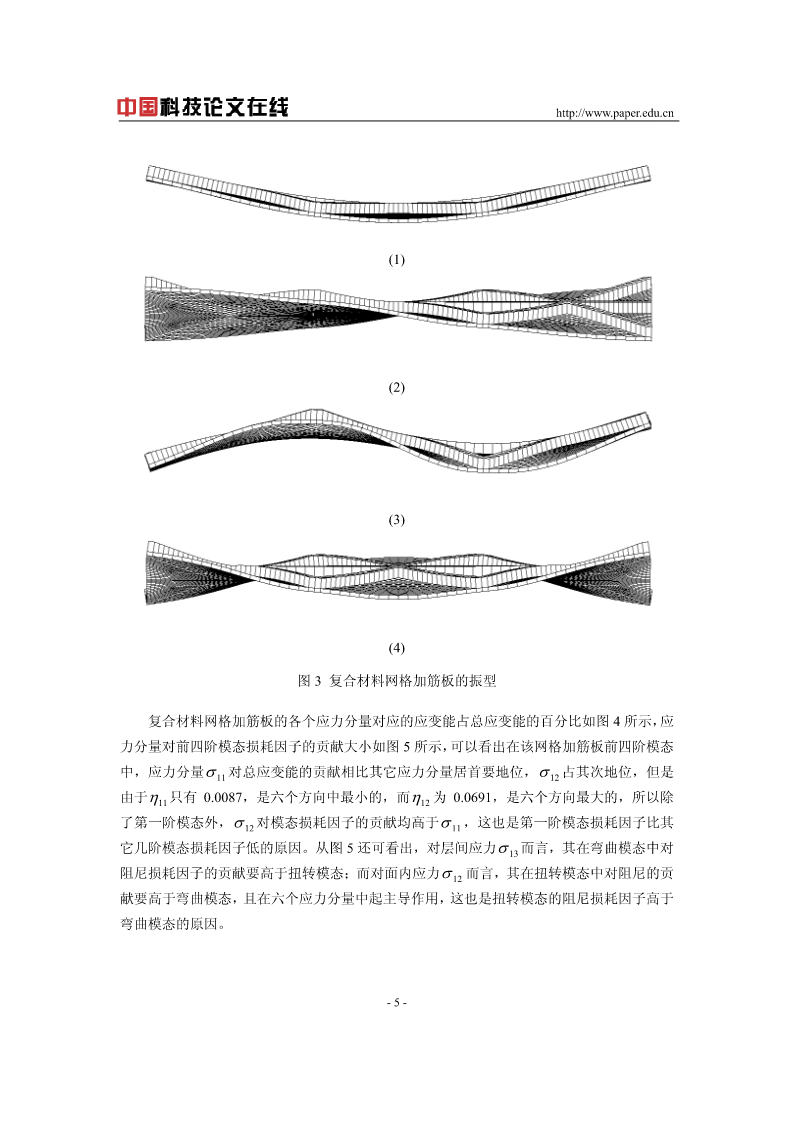
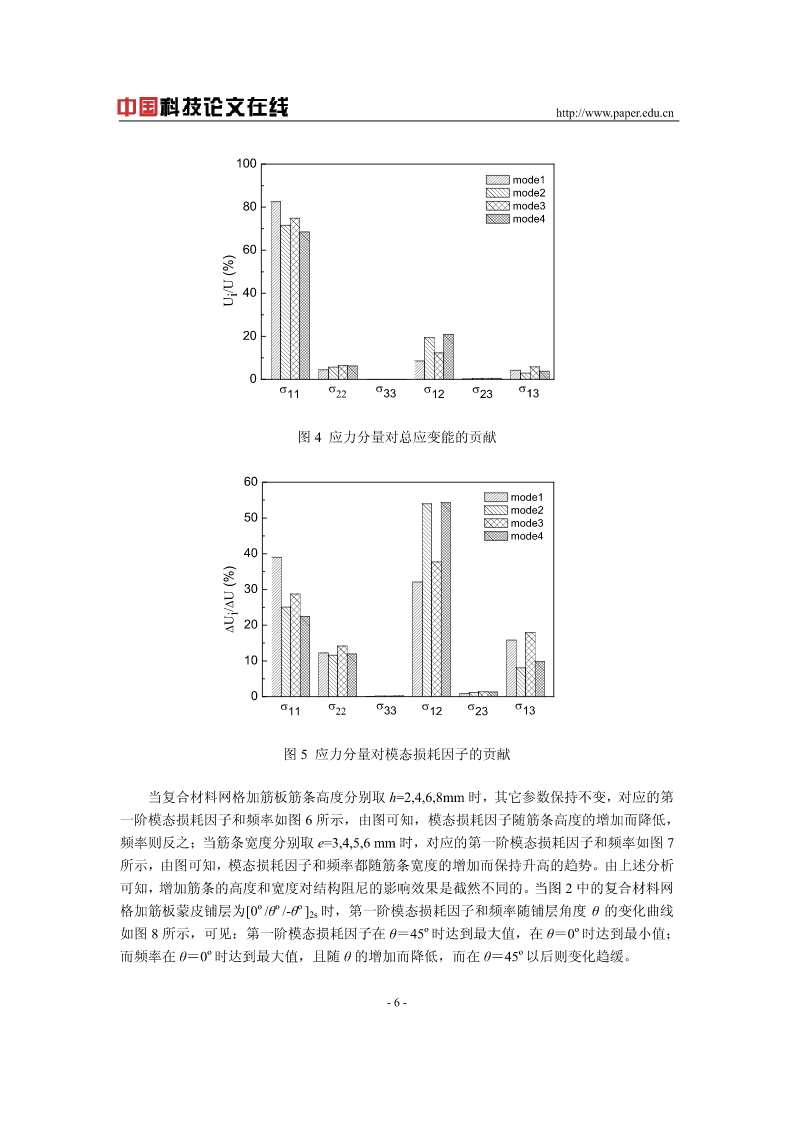
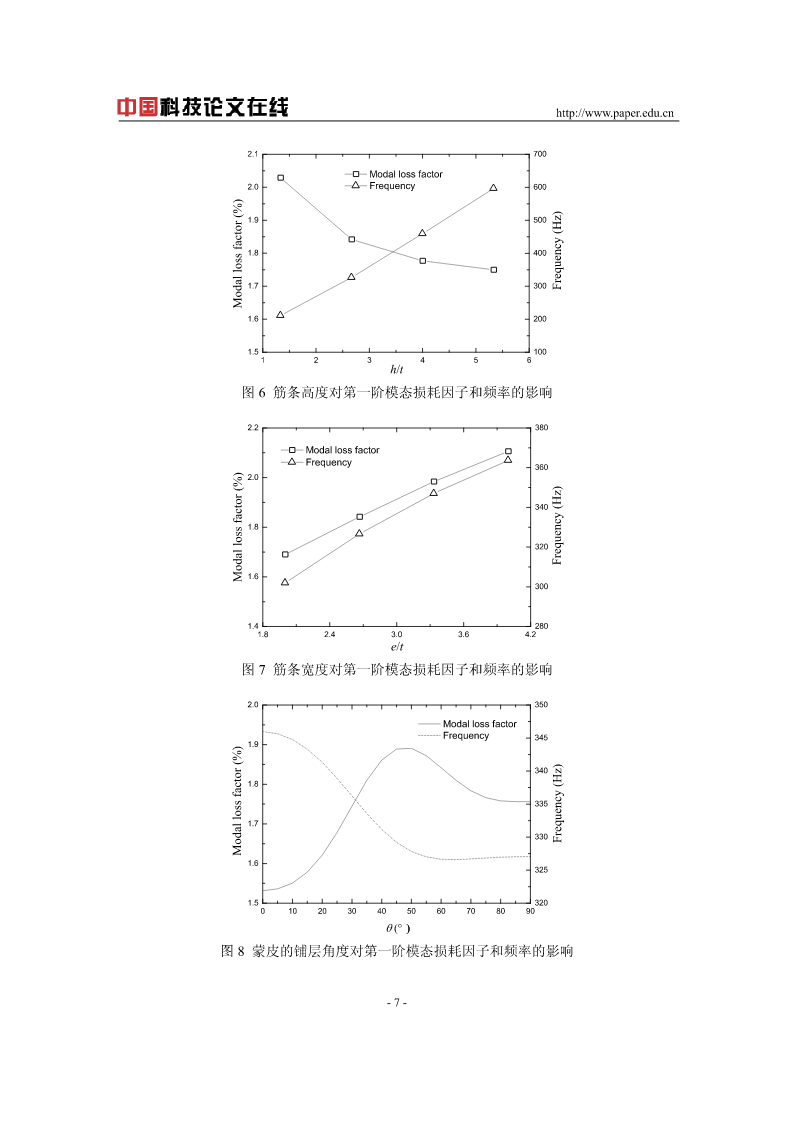


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

复合材料网格加筋结构的阻尼特性研究.pdf
http://www.paper.edu.cn*复合材料网格加筋结构的阻尼特性研究张少辉,陈花玲西安交通大学机械工程学院振动与噪声控制研究所,陕西,西安(710049)E-mail:zsh@mailst.xjtu.edu.cn摘要:复合材料网格加筋结构是一种在航空航天应用领域常见的结构形式,本文应用基于应变能的有限元方法研究了复合材料网格加筋结构的阻尼特性,此方法从单向复合材料的阻尼性能参数出发,通过有限元模态分析得到复合材料结构的模态损耗因子,同时还可以比较三维应力分量对阻尼的贡献。最后考察了蒙皮的铺层

复合材料网格加筋结构可靠性分析.docx
复合材料网格加筋结构可靠性分析标题:复合材料网格加筋结构可靠性分析引言:复合材料网格加筋结构在航空航天、汽车、船舶等领域具有广泛的应用。然而,随着结构的复杂化和工作条件的变化,加筋结构在使用过程中可能出现失效和损伤。因此,对于复合材料网格加筋结构的可靠性进行分析具有重要意义。一、复合材料网格加筋结构的构造和特点A.复合材料网格加筋结构的定义和分类B.复合材料的性质和优势C.网格加筋的优缺点二、复合材料网格加筋结构的失效模式和原因分析A.失效模式的分类和描述B.失效原因的分析与解释C.失效模式与应力分布的关

复合材料加筋板剪切屈曲特性研究.docx
复合材料加筋板剪切屈曲特性研究复合材料加筋板剪切屈曲特性研究摘要:复合材料加筋板是一种常见的结构元素,在航空、航天、汽车、建筑等领域有着广泛的应用。了解加筋板的剪切屈曲特性对于预测其结构性能和优化设计具有重要意义。本文通过对复合材料加筋板的剪切屈曲现象进行分析,探讨不同加筋形式、加筋材料和几何尺寸对其剪切屈曲特性的影响。研究结果显示,加筋板的剪切屈曲受到加筋形式和加筋比例的显著影响,而加筋材料和几何尺寸的影响并不显著。因此,在设计复合材料加筋板时,应注重选择合适的加筋形式和合理的加筋比例,以提高其剪切屈曲

加筋土结构筋-土界面特性研究进展.docx
加筋土结构筋-土界面特性研究进展AbstractReinforcedsoilstructureshaveemergedasapopularformofretainingstructuresduetoitsexcellentstabilityandversatility.Theperformanceofreinforcedsoilstructureslargelydependsontheinterfacepropertiesbetweenthesoilandreinforcement.Thispaperpr

加筋土结构动力特性研究现状综述.docx
加筋土结构动力特性研究现状综述概述加筋土结构是一种新型土的工程材料。加筋土结构具有高耐久性、优良的抗震性能和变形能力等特性,已被广泛应用于建设领域中。随着人们对该结构更加深入的研究,其动力特性的研究也被赋予了更高的重要性。本文综述了目前加筋土结构动力特性的研究现状,旨在为加强加筋土结构抗震能力提供参考。加筋土结构的基本特征加筋土是指在天然土中加入合适的工艺材料,以改善土的性质。加筋土结构的基本特性是具有减小因地震而引起的土体体积变化的能力,提高其抗震性能。因此,加筋土结构被广泛应用于地震区域。加筋土结构的
