常功率平面热源法测定绝热材料的导热系数λ和导温系数a.pdf

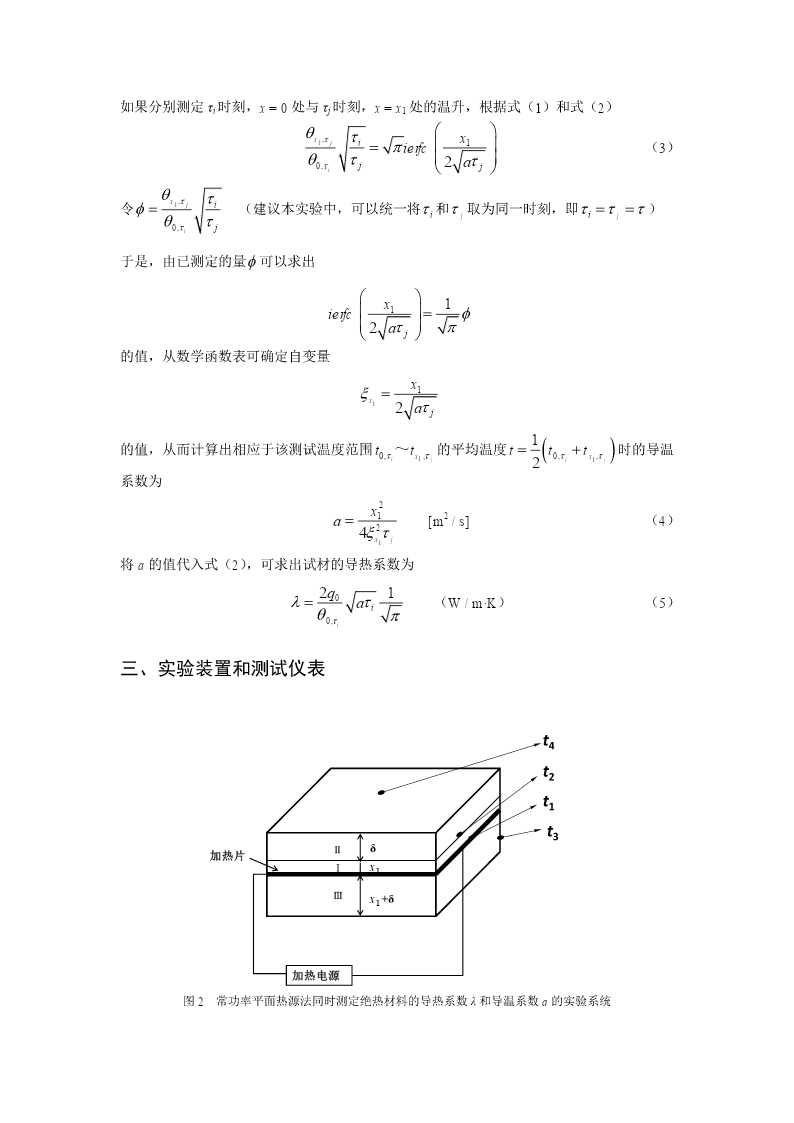
常功率平面热源法同时测定绝热

材料的导热系数λ和导温系数a

一、实验目的与任务

1.巩固和深化对非稳态导热理论的理解，更直观地认识非稳态导热过程中温度的变化。
2.学习用常功率平面热源法同时测定绝热材料的导热系数λ和导温系数a的实验方法和技
能。
3.掌握获得非稳态温度场的方法。
4.加深理解导热系数λ和导温系数a对温度场的影响。

二、实验原理

x=0

x1

x

图1

根据非稳态导热过程的基本理论，在初始温度t0分布均匀的半无限大的物体中，从τ=0
2
起，半无限大的物体表面（即图1中x=0的平面）受均匀分布的平面热源q0（W/m）的

作用，在常物性条件下，离表面x处的温升θx,τ=tx,τ-t0为：
2qx
0（）
x,aierfc1
2a

x
令
2a

ierfcξ代表变量ξ的高斯误差补函数的一次积分，即：

ierfcerfcd

τ>0，但x=0时，
x1
ierfcierfc0
2a
于是由式（1）可知
2q1
0a（2）
0,
如果分别测定τi时刻，x=0处与τj时刻，x=x1处的温升，根据式（1）和式（2）

x,x
1jiierfc1（3）
2a
0,ijj

x,
令1ji（建议本实验中，可以统一将和取为同一时刻，即）
ijij
0,ij

于是，由已测定的量可以求出

x1
ierfc1
2a
j
的值，从数学函数表可确定自变量
x
1
x1
2aj
1
的值，从而计算出相应于该测试温度范围tt～的平均温度ttt时的导温
0,ijx1,20,ijx1,
系数为
x2
a1[m2/s]（4）
42
xj1
将a的值代入式（2），可求出试材的导热系数为
2q1
0a（W/m·K）（5）
i
0,i

三、实验装置和测试仪表

t4

t2

t1

t3
Ⅱδ
加热片
Ⅰx1

Ⅲ
x1+δ

加热电源

图2常功率平面热源法同时测定绝热材料的导热系数λ和导温系数a的实验系统

试材Ⅰ、Ⅱ、Ⅲ的材料相同，其厚度分别为x1、δ和x1+δ。试材Ⅰ的长宽是厚度的8～
10倍。试材Ⅰ和Ⅲ之间放置一个均匀的平面加热片。电加热片用直流稳压电源供电。
在试材Ⅰ的上、下表面中间分别装有铜－康铜热电偶2和热电偶1，用以测试试材Ⅰ上、

下表面的温度t2和t1；热电偶3和热电偶4则分别用来测试试件周围的温度环境t3和试材Ⅱ

的上表面温度t4。
由于采用对称加热面方法，平面热源的热功率实际为总加热功率的一半：

U2
q[W/m2]（6）
02RF
式中，U为加热电压；R为加热片电阻；F为加热片面积。

四、实验步骤

1.测出试材Ⅰ的厚度x1[m]。
2.安装热电偶及试材。将热电偶2和1分别贴在试材Ⅰ的上下表面中间位置处，热电偶3
贴在加热片的边上，热电偶4贴在试材Ⅲ的上表面中间位置。组装好试材，罩上有机玻
璃罩。
3.仔细检查各接线线路和热电偶测量线路。

4.记录实验箱编号、加热片电阻R、加热面积F以便计算平面热源功率。记录t2测点距热

源距离x1,记录初始时刻的t1、t2、t3、t4；
5.打开直流稳压加热电源，调节加热电压，其中，编号为1、2、9、10的实验箱加热电压
为15V，其余实验箱加热电压为20V，给加热器上电并开始计时。

6.加热过程中监测绝热材料顶端温度测点t4是否发生变化，如果不发生变化，则满足半无

限大物体导热的规律，每隔2分钟记录一组四个温度值t1、t2、t3、t4，共记录10组。

五、预习要求

仔细阅读实验指示书，弄清楚的计算方法；复习一下非稳态导热问题的理论分析和数值
解法，分析λ和a对非稳态导热过程的影响。

六、实验报告

1.实验装置系统简图。
2.根据实验过程中计算机采集到的原始数据，计算τ=600s和720s时的导热系数λ和导
温系数a。

3.根据实验结果画图：（1）热源温度t1和距热源x1处温度t2随时间τ的变化关系曲线；（2）
导热系数λ随时间τ的变化曲线；（3）导热系数a随时间τ的变化曲线。并结合物性和
导热机理对（2）和（3）的变化规律进行分析。

4.根据半无限大物体非稳态导热理论解，结合实验条件（x1,q0,τ等参数均取本次实验值），
作图分析λ和a值对非稳态导热过程的影响：（1）固定λ，改变a（a取不同的量级），

研究a对t2~τ温升曲线的影响；（2）固定a，改变λ（λ取不同的量级），研究λ对t2~
τ温升曲线的影响。
附：高斯误差补函数的一次积分表

xierfc(x)xierfc(x)xierfc(x)x