标准渐开线齿轮直齿圆柱齿轮啮合传动.pdf

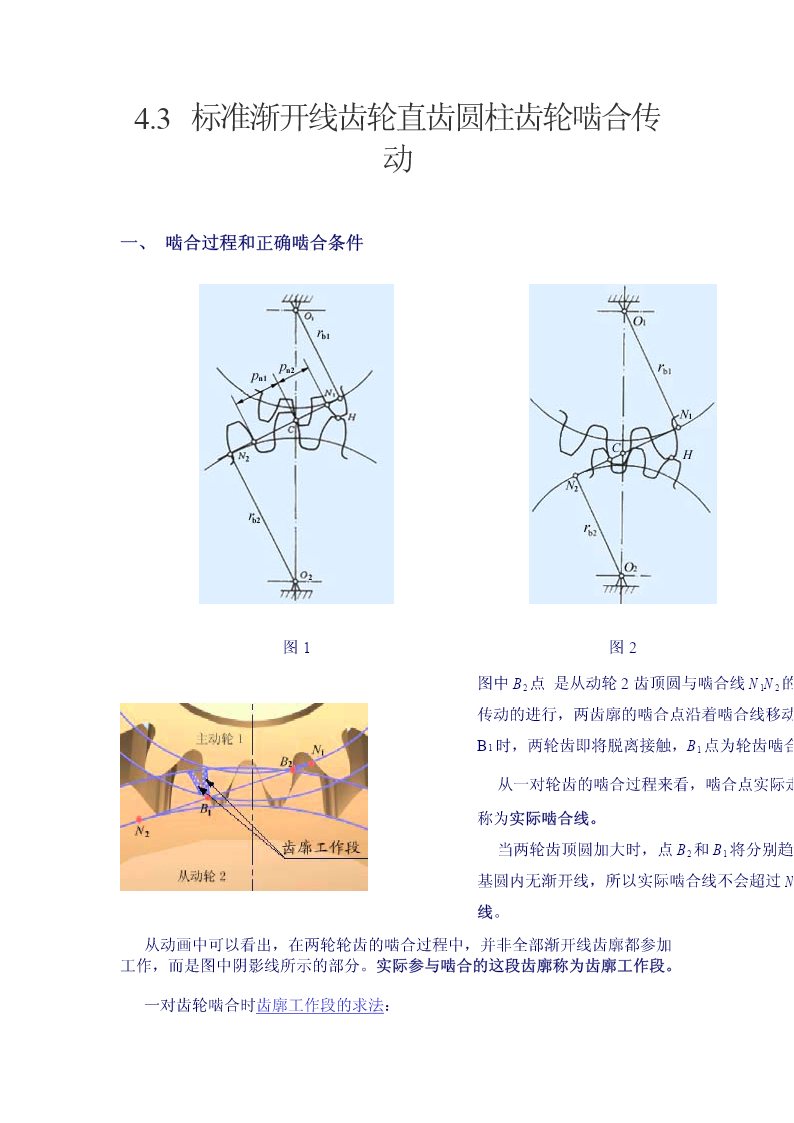
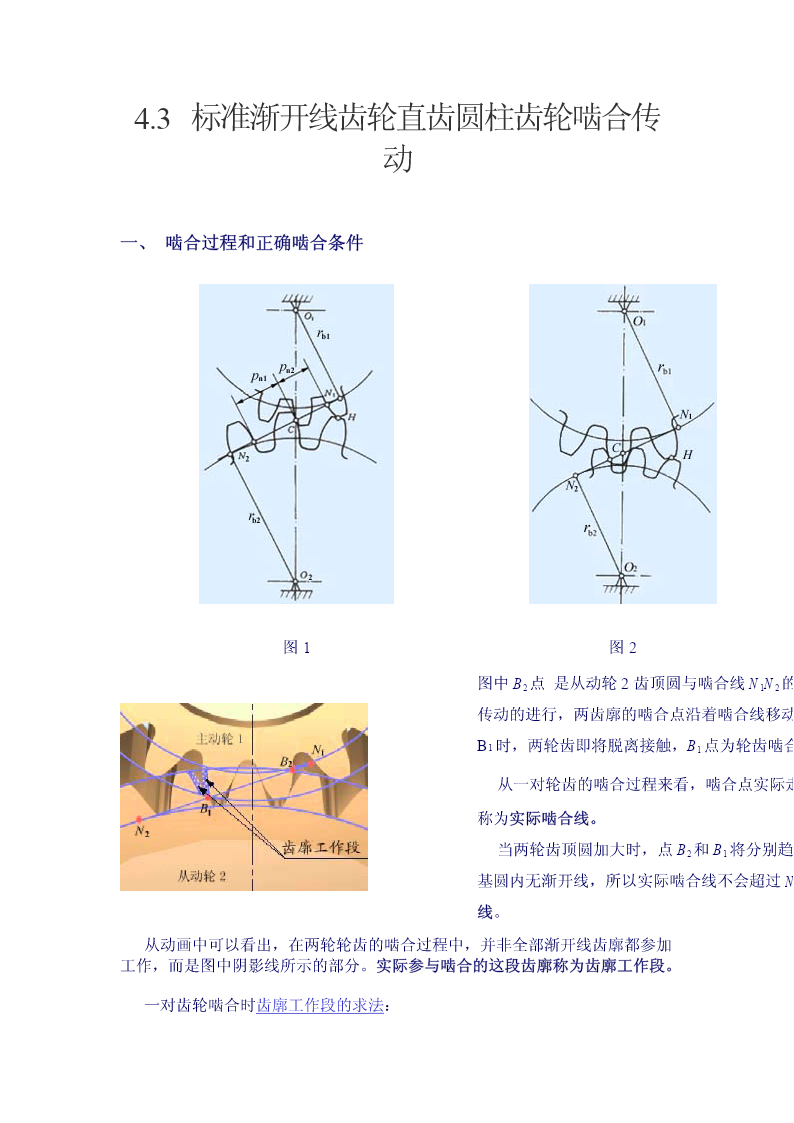
4.3标准渐开线齿轮直齿圆柱齿轮啮合传

动

一、啮合过程和正确啮合条件

图1图2

图中B2点是从动轮2齿顶圆与啮合线N1N2的
传动的进行，两齿廓的啮合点沿着啮合线移动

B1时，两轮齿即将脱离接触，B1点为轮齿啮合

从一对轮齿的啮合过程来看，啮合点实际走

称为实际啮合线。

当两轮齿顶圆加大时，点B2和B1将分别趋

基圆内无渐开线，所以实际啮合线不会超过N
线。

从动画中可以看出，在两轮轮齿的啮合过程中，并非全部渐开线齿廓都参加
工作，而是图中阴影线所示的部分。实际参与啮合的这段齿廓称为齿廓工作段。

一对齿轮啮合时齿廓工作段的求法：

三个图中的齿轮都是渐开线齿轮，但图1和图2中的主动轮只能带动从动轮转过一个小角度就
动从动轮整周转动，看来并不是任意两个渐开线齿轮都能正确地进行啮合，而是必须满足一定的条

什么？

从图3中可以看出：两个渐开线齿轮在啮合过程中，参加啮合的轮齿的工作一侧齿廓的啮合点都

工作一侧齿廓的啮合点H不在啮合线N1N2上，这就是两轮卡死的原因。
从图3中可以看出

是齿轮1的法向齿矩，是齿轮2的法向齿矩，亦即:

这个式子就是一对相啮合齿轮的轮齿分布要满足的几何条件,称为正确啮合条件。

由渐开线性质可知，法向齿距与基圆齿距相等，故上式也可写成

将和代入式中得：

由于模数m和压力角均已标准化，不能任意选取，所以要满足上式必须使：

结论：一对渐开线齿轮，在模数和压力角取标准值的情况下，只要它们分度圆上的模数和压力角

二、齿轮传动的正确安装条件

1、齿侧间隙

为了避免齿轮在正转和反转两个方向的传动中齿轮发生撞击,要求相啮合的轮
齿的齿侧没有间隙。

齿侧间隙沿两轮的节圆来测量，无测隙要求：，

即无齿侧间隙啮合条件为：一个齿轮节圆上的槽宽等于另一个齿轮节圆上的齿
厚。
2、标准安装
如图所示为满足正确啮合条件的一对外啮合标准直齿圆柱齿轮，它的中心距
是两轮分度圆半径之和，此中心距称为标准中心距。

啮合线N1N2与O1O2的交点C是啮合节点，而两轮分度圆也相切于C点，所
以分度圆与节圆重合为一个圆。即

由于标准齿轮的分度圆齿厚与槽宽相等，因此

结论：两个标准齿轮如果按照标准中心距安装，就能满足无齿侧间隙啮合条
件，能实现无齿侧间隙啮合传动。

从图中可以看出一轮齿顶与另一轮齿根之间有一个径向间隙c，我们称为
顶隙，它是为储存润滑油以润滑齿廓表面而设置的，这就是标准齿轮齿根高大于

齿顶高的原因，并因此把c*称为顶隙系数。在上述的安装情况下c＝c*m，c*m称
为标准顶隙。

一对标准齿轮按照标准中心距安装，我们称之为标准安装。

3、非标准安装
两轮的实际中心距不等于标准中心距。这时节圆与分度圆不重合，节圆半径
也不等于分度圆半径，其啮合角也不等于分度圆的压力角。

标准中心距为

'''acosα
a=r1+r2=
实际中心距为cosα'

4、齿轮与齿条传动的标准安装

1）标准安装：齿轮的分度圆与齿条的中线相切，称这种安装为标准齿轮与齿

条的标准安装。

在标准安装的情况下，节点C是齿条中线与分度圆的切点，此时，齿轮分度

圆与节圆重合，齿条中线与节线重合；啮合角等于分度圆压力角。

由于标准齿轮分度圆上的齿厚等于槽宽，齿条中线上的齿厚也等于槽宽，且

均等于。

结论：标准齿轮和齿条如果是标准安装，就能满足无齿侧间隙啮合条件，能
实现无齿侧间隙啮合传动。

2）非标准安装：齿轮的分度圆与齿条的中线不相切，出现侧隙。

从图中可以看出，齿轮和齿条将只有一侧接触，另一侧出现间隙。但由于啮

合线不变，因而节点C不变，故：齿轮节圆与分度圆仍重合，但齿条节线与中

线不再重合；啮合角等于分度圆压力角。这种安装称为非标准安装。

从上面的分析可以发现，当齿轮与齿条啮合传动时，无论是标准安装还是非

标准安装都具有下面两个特点：

1.齿轮分度圆永远与节圆重合，；

2.啮合角永远等于分度圆压力角，。

三、渐开线齿轮机构连续传动的条件

1.轮齿啮合过程

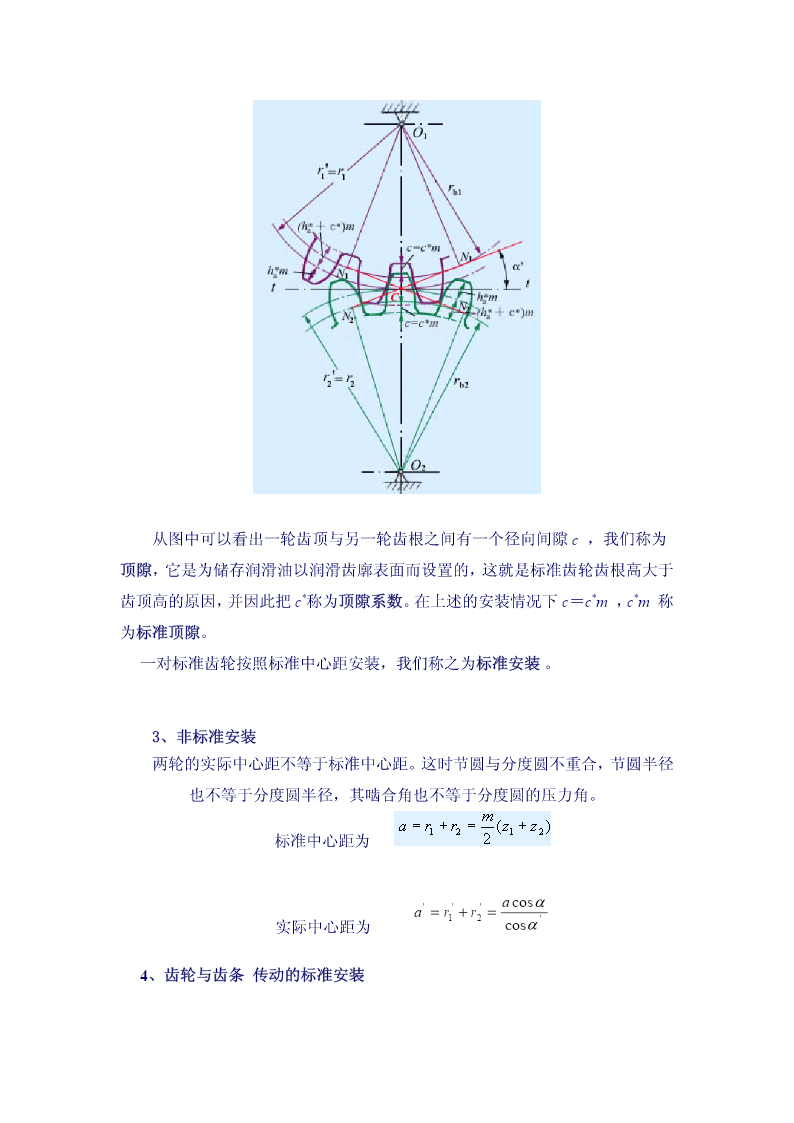
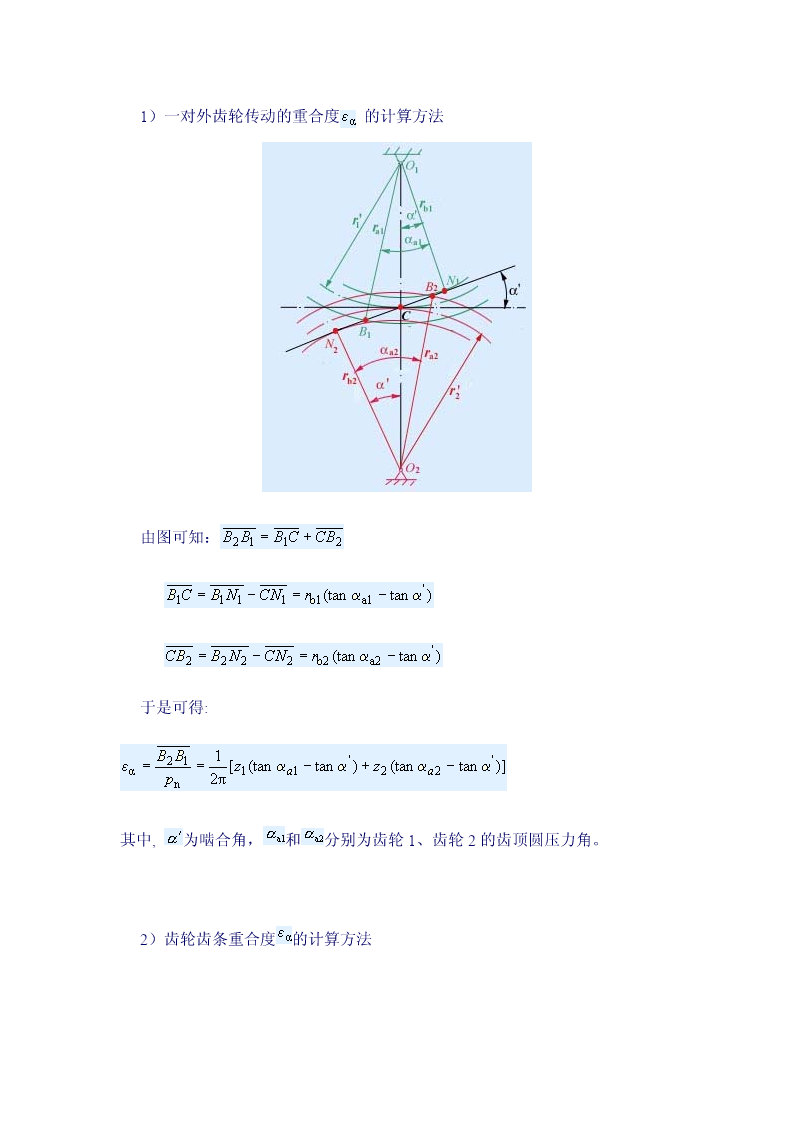
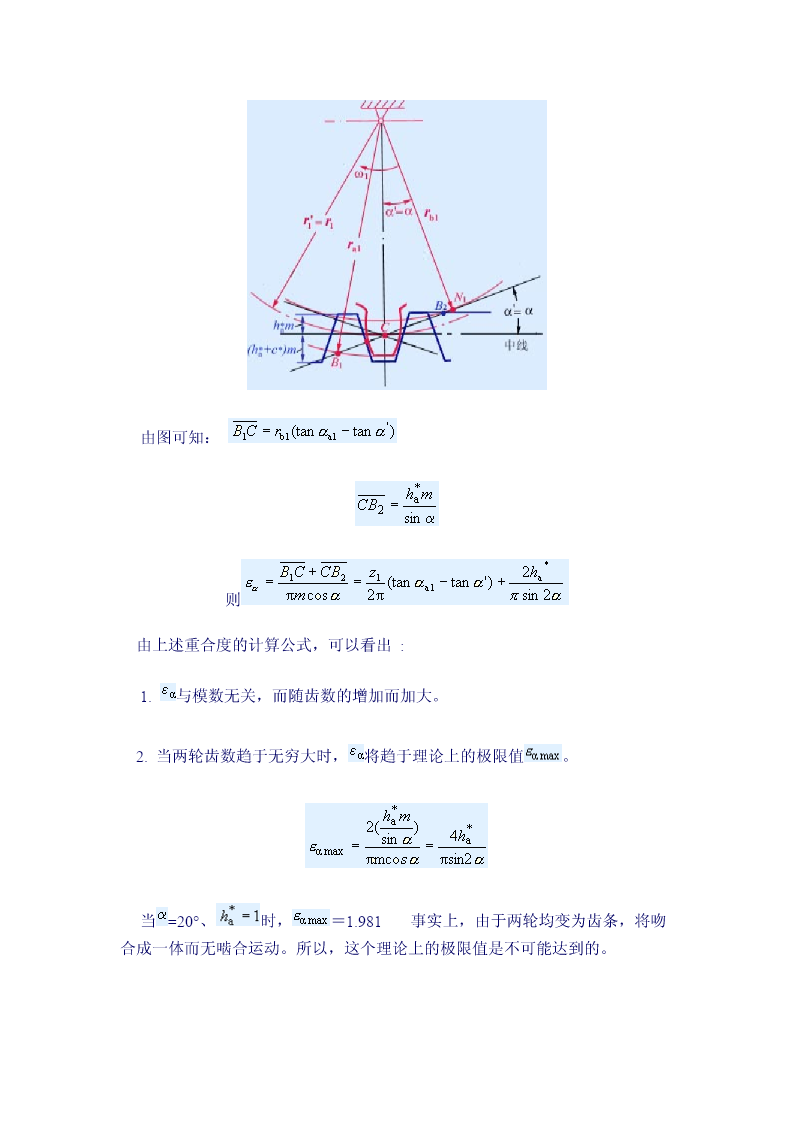
图中B2点是从动轮2齿顶圆与啮合线N1N2的交点，是一对轮齿啮合的起始

点。随着啮合传动的进行，两齿廓的啮合点沿着啮合线移动，直到主动轮1的

齿顶圆与啮合线的交点B1时，两轮齿即将脱离接触，B1点为轮齿啮合的终止点。
从一对轮齿的啮合过程来看，啮合点实际走过的轨迹只是啮合线上的一段，

即，称为实际啮合线。

当两轮齿顶圆加大时，点B2和B1将分别趋近于点N1和N2，实际啮合线将加

长，但因基圆内无渐开线，所以实际啮合线不会超过N1N2，即N1N2是理论啮合

线，称为理论啮合线。

从动