
第7章 矩量法.ppt

kp****93








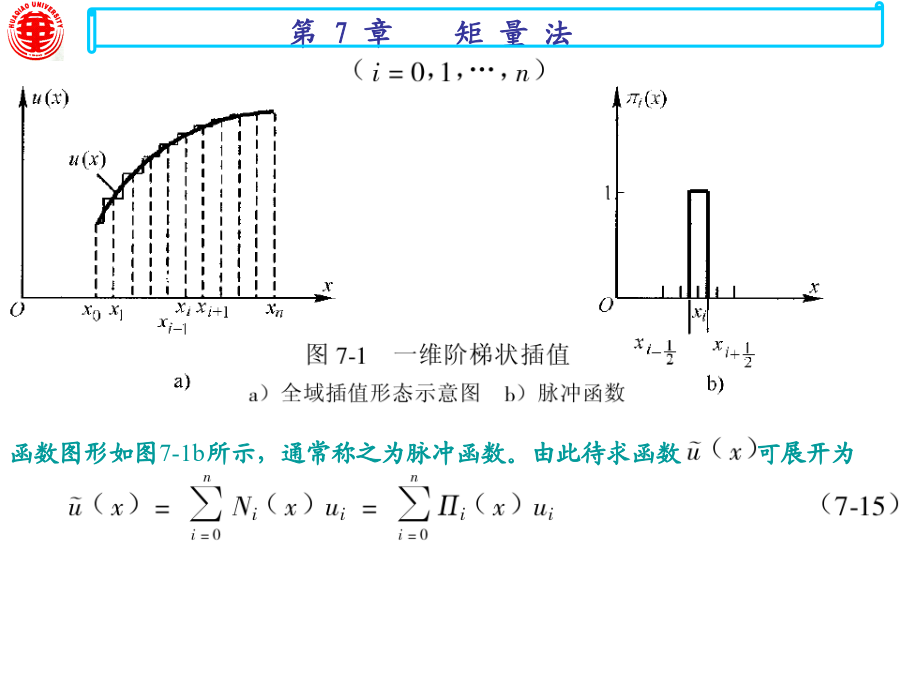
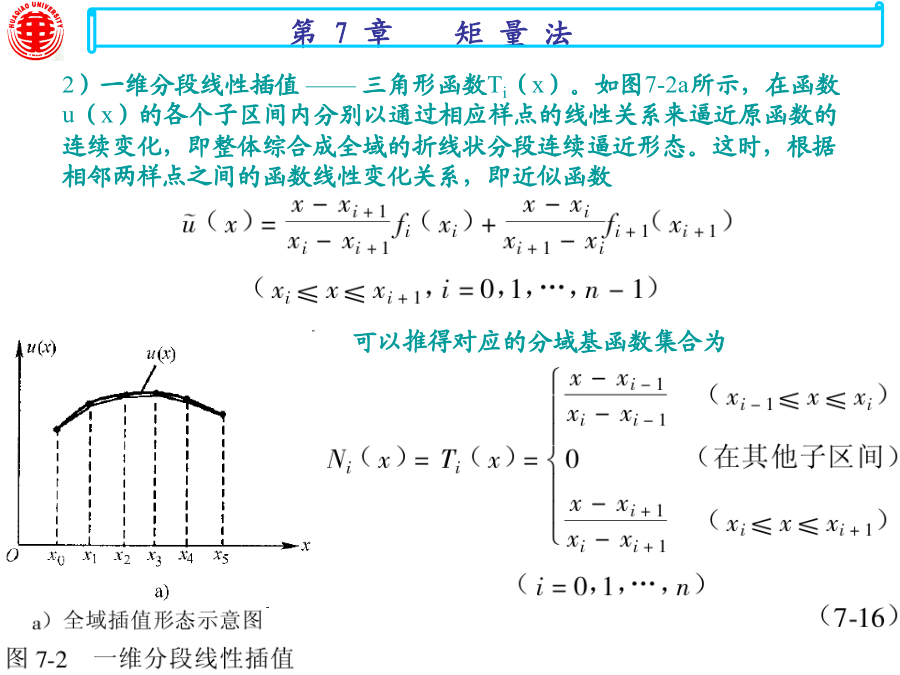
亲,该文档总共48页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第7章 矩量法.ppt
第7章矩量法矩量法的数学处理过程可以采用加权余量法或定义泛函内积等方法展开R。F.Harrington对用矩量法求解电磁场问题作了全面和深入的分析,其经典著作已于1968年出版[1]。为从数学意义上,既能理解通常矩量法构造的数学基础,又能把握其他数值计算方法与之相关的内在联系,本书采用加权余量法的概念来说明矩量法。加权余量法(TheMethodofWeightedResiduals)的概念首先由S.H.Crandall[2]在1956年提出。他将由积分、微分方程离散化为矩阵方程(代数方程组)的方法,统一归

第10章--矩量法0.doc
第十章矩量法解析方法仅适用于结构简单得散射体。如果散射目标结构复杂,必须选用数值方法。数值方法就是对所求解得微分方程或积分方程实施离散,采用一组基函数表示电场、磁场或感应电流等未知量,然后将电磁场微分方程或积分方程转换为一组线性代数方程,即可按照标准得数值程序求解这些线性方程组。数值方法得优点在于容易处理结构复杂得散射体,而且通常可以获得高精度解。随着高性能计算机得飞速发展,数值方法已经成为解决实际问题得日益重要得工具。现今已有多种数值方法,各具特色,分别适用于求解不同得电磁问题。典型得数值方法就是矩量法

矩量法英文2.ppt
LimitationofPulseBasis/DeltaTestingDiscretization:TE-WaveEFIEFurtherExplanationDiscussionsDiscussionsTEWaveScatteringfromPECStripsorCylinders–EFIEUseofEFIEFormulationofEFIETriangularBasisFunctionPulseDoubletTestingFunctionMatrixEquationBistaticCrossSectio

矩量法作业DOC.docx
摘要矩量法是将连续方程离散为代数方程组的方法,此法对于求解微分方程和积分方程均适用。本文以直立的线天线为例,详细介绍了矩量法的基本思想及原理、基函数以及检验函数的选择,系统阐述了直立的天线的双位积分方程的建立过程,最后利用矩量法求解双位积分方程、使用matlab编程实现得到直立的天线上的电流分布。本文采用1.77λ的线天线的频率是0.3GHz,采用矩量法所选用的基函数是正弦函数,检验函数是函数。关键字:线天线;矩量法;双位积分方程引言计算电磁学被广泛地定义为一门内在和常规地应用数字计算机来获得电磁问题的数

海伦积分方程的矩量法求解.docx
海伦积分方程的矩量法求解一、课题研究内容利用矩量法求解表述对称天线上电流分布的海伦积分方程。本课题研究的是半波天线上的电流分布,并采用点选配法对海伦积分方程求解,最后得到天线上的电流分布图。海伦积分方程为:。(1)二、解决方案图1所示是对称天线,根据矩量法原理,待求电流可表示为:(2)这里为简单起见,只取到N=2.选取这样的基函数是考虑到它可以满足细导体末端电流为零的边界条件,式中为天线的一般长度,为待定系数,在轴线上,为源的坐标。图1检验函数选择狄拉克函数,即。将(2)式代入(1)式,并整理,可得(3)
