专题1 函数的性质与应用.ppt

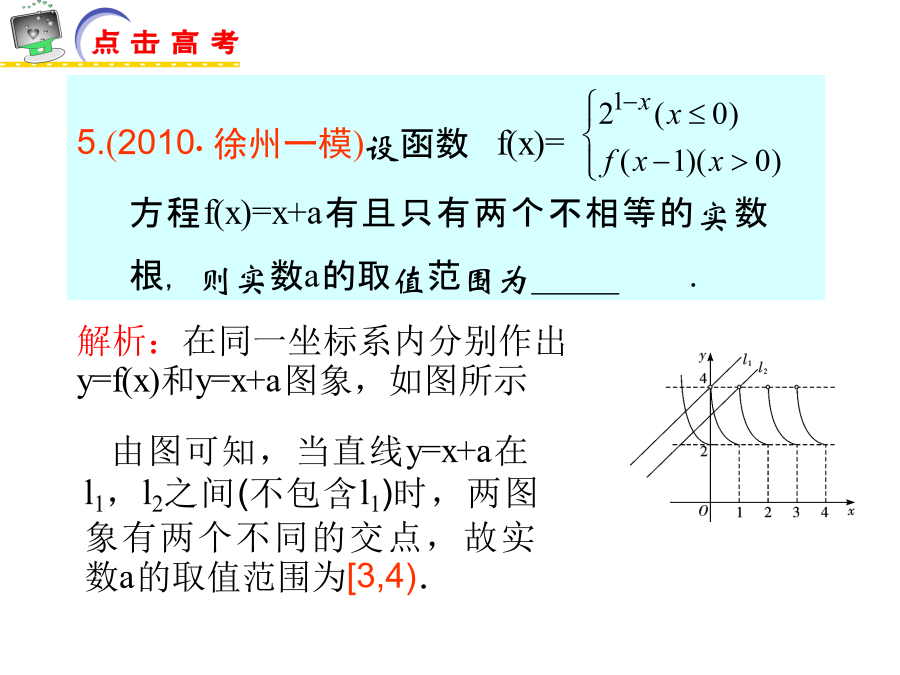
2.(2010●海安中学)奇函数f(x)在区间[3,7]上是增函数，在区间[3,6]上的最大值为8，最小值为-1，则2f(-6)+f(-3)=_____4.(2010●江苏卷)设函数f(x)=x(ex+ae-x)(x∈R)是偶函数，则实数a的值为_____5.(2010●徐州一模)设函数
例1.已知是否存在实数a，b，c，使f(x)同时满足下列三个条件：
①定义域为R上的奇函数；
②在[1，+∞)上是增函数；
③最大值为1.
若存在，求出a，b，c的值；若不存在，说明理由分析：先“脱”去对数符号“log”，利用①中的奇函数的条件求出a，b，c所满足的一些条件或值，然后利用条件②进一步确定出待求系数所应满足的条件，最后利用条件③求出满足条件的值或说明其不存在．，
于是(x2+1)2-a2x2=(x2+1)2-c2x2
所以a2=c2，即a=c或a=-c.
当a=c时，f(x)=0，不合题意，故舍去
从而a=-c
于是在[1，+∞)上是增函
数．
令因为在[1，+∞)与(-∞，-1]上是增函数，且当x＞1时，＞0，当x＜-1时，＜0，故仅当c＞0时，f(x)与g(x)的单调性相同，从而当x=-1时，在(-∞，-1]取得最大值-2，此时由f(x)的最大值为1知，g(x)的最大值为3，
于是解得c=1，从而a=-1，b=1，满足题设条件的a，b，c存在，且它们的值分别为-1,1,1.变式1.已知是否存在实数p、q、m，使f(x)同时满足下列三个条件：
①定义域为R的奇函数；
②在[1，+∞)上是减函数；
③最小值是-1.
若存在，求出p、q、m；若不存在，说明理由．因为在[1，+∞)上递增，在(-∞，-1]也递增，只有m＞0时，在[1，+∞)上g(x)递增，从而f(x)递减．
于是，x=-1时，在(-∞，-1]上取得最大值-2，
此时由f(x)的最小值为-1，得g(x)的最大值为3.
从而
存在p=-1，q=1，m=1.例2.已知二次函数f(x)=ax2+bx+1和函数
(1)若f(x)为偶函数，试判断g(x)的奇偶性；
(2)已知方程g(x)=x有两个不等的实根x1，x2(x1<x2)．
①证明函数f(x)在(-1,1)上是单调函数；
②若方程f(x)=0的两实根为x3，x4(x3<x4)，求使
x3<x1<x2<x4成立的a的取值范围．解析：(1)因为f(x)为偶函数，所以f(-x)=f(x)，所以bx=0，所以b=0.
所以，所以函数g(x)为奇函数②x1，x2是方程(*)的根，所以a2x12+bx1+1=0
所以bx1=-a2x12-1，同理bx2=-a2x22-1
所以f(x1)=ax12+bx1+1=ax12-a2x22=(a-a2)x12
同理f(x2)=(a-a2)x22

例3.定义在R上的单调函数f(x)满足f(3)=log23且对任意x，y∈R都有f(x+y)=f(x)+f(y)．
(1)求证f(x)为奇函数；
(2)若f(k·3x)+f(3x-9x-2)＜0对任意x∈R恒成立，求实数k的取值范围．1．函数值域的常用求法：配方法、分离变量法、单调性法、图象法、换元法、不等式法等．无论用什么方法求函数的值域，都必须考虑函数的定义域．另外在解题过程中经常用到分类讨论、等价转化等数学思想方法．3．函数的单调性、奇偶性、周期性是高考的重点内容之一，考查内容灵活多样．判断函数的奇偶性与单调性方法：若为具体函数，严格按照定义判断；若为抽象函数，用好赋值法，注意赋值的科学性、合理性．复合函数的奇偶性、单调性求解的关键在于既把握复合过程，又掌握基本函数的性质．1．函数的性质都要建立在定义域基础上，解题时首先要考虑定义域．
2．函数性质的探求，大多利用定义．
3．解题策略上常常考虑特例探路，图象辅佐。