现代数学与应用.ppt

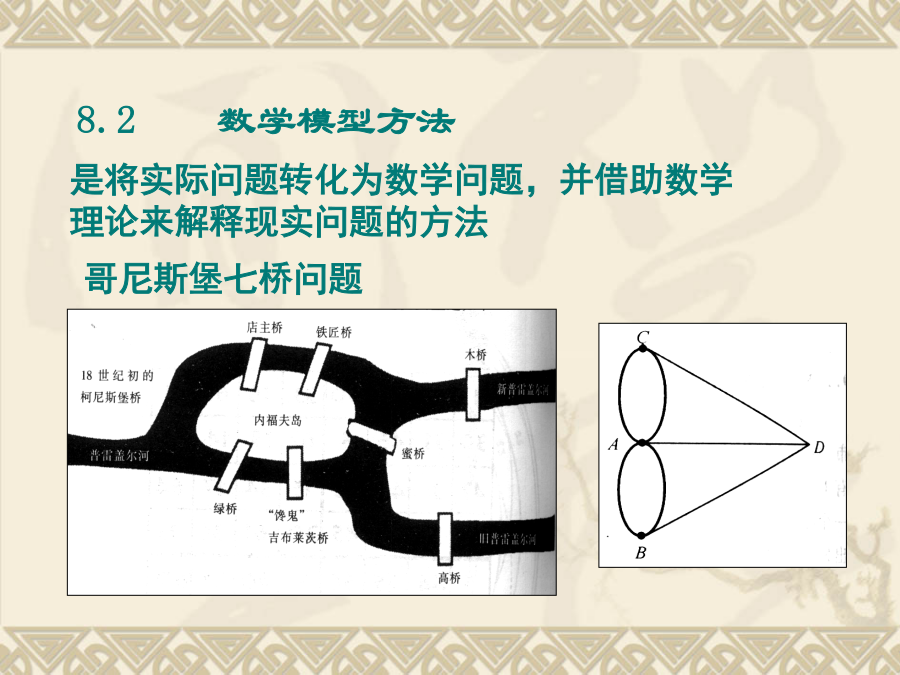
8.120世纪数学应用的发展概况20世纪下半叶，是应用数学发展的高峰期:
突变理论、模糊数学以及计算机数学应运而生.
数学应用受到社会的关注并取得前所未有的发展
数学与其它领域相结合而形成一系列交叉学科8.2数学模型方法用数学模型方法解决实际问题，主要经历以下的几个步骤：生态学中应用的范例:数学模型给出的结果，可以给这一现象解释如下：8.3非线性数学
非线性问题没有一般的求解方法。往往很难求得准确解，常采用线性逼近的方法求得非线性问题的近似解。例如：“拟线性”的方法。
人口增长数学模型：从线性方程到非线性方程按照这个模型考察短期人口的增长情况，基本是正确的。但是用它未预见更长一段时期的情况，就很难奏效。比如，
1965年1月的世界人口是33.4亿，由于1960年至1970年世界人口的平均增长率为2%。按马尔萨斯的模型计算，到2660年，世界人口将达到3.6×107亿。这样，即使我们把占地球面积80%的水面也住上人，届时每个人的肩上也得站两个人。逻辑斯蒂模型，一个非线性方程及其解:其中c＞0是常数，它由t0时的人口数x0=α/(β+c)确定。当t趋于无穷大时，x趋于α/β。这表示在资源有限的区域内，人口不能无限制地增长，它要趋于一个饱和值（α/β）。
按照逻辑斯蒂模型计算，地球总人数的饱和值估计将是107.6亿，而按照这一模型曲线，在人口达到这个饱和值的一半之前，是人口加速增长时期；达到其一半之后，人口增长率就降低，进入减速增长时期，最终的增长率趋于零。量子场理论____麦克斯韦方程___杨——米尔斯方程1967年，杨振宁在研究规范场理论的推广问题时，发现了黎曼几何中的公式规范场公式的特例。1975年初杨振宁听了一系列数学讲座，开始使用纤维丛理论解释物理现象，并于当年发表了论文,明确指出了纤维丛理论和规范场理论的联系，将这两个领域的概念建立了一一对应的关系8.5折叠与突变理论

突变现象则是自然界和社会中普遍存在的另一类不具有稳定状态的客观现象，最简单的突变模型：f(x)=(1/3)x3，在x=0处，给出一个微扰，形成了一个函数族fa(x)=(1/3)x3+ax尖角型模型的实例——气液相变中的突变现象水的密度ρ是温度T和压力P的函数整个行为曲面由液态的高密度区向气态的低密度倾斜，说明随温度上升和压力下降，密度变小8.6平衡点与对策论
有鞍点的零和对策实例利用所谓的“支付矩阵”说明双方最佳的选择方案对于同盟国一方：如果沿北线搜索，那么不管日方走哪条路增援，他取得的支付都是2（即获得2天的轰炸时间）；如果同盟军沿南线搜索，那么可以获得支付1或3。在事先不知日方确切的增援线路的情况下，同盟国的决策是从北线搜索，并获得支付2。如果将支付矩阵中每行的支付的“极小值”列在图的右侧，可以看出，同盟国是选择了“行极小中的最大值”。
出于相同的理由，日方会选择北线增援，即选择了列局中人的“列极大中的最小值”（见图的下方）。在局中人的这种选择下，不管对方采用什么行动，双方都获得了自己的一种极小的支付。在双方的这种抉择下，双方的支付都是2，，即列极小中的最大值等于列极大中的最小值，我们称它为对策的“平衡点”。由于对竞争双方而言支付的绝对值相等，且符号相反，因此又称此类对策的解为“零和对策”，平衡决策点又称为“鞍点”从数学的观点上看，极大极小定理对于竞争双方的零和对策，已经提供了唯一的数值解。但在现实中，对策的局中人可能不只是两个，或者局中人赢得的支付又未必等于另一局中人输掉的支付
美国数学家纳什将极大极小定理推广到了有两个或更多个局中人的非零和对策——所谓的“非合作对策”的情景。并得到了重要的结论——纳什定理：在任意一个n个人参加的非合作对策（零和或非零和）中，如果每个局中人有有限个纯策略，那么，至少有一个策略平衡组。
纳什的工作于1994年获得了经济学诺贝尔奖，这是在使诺贝尔奖建立93年之后，第一次授予了一个纯数学理论研究成果。8.7隶属函数与模糊数学（1965年．美国的扎德）式中的x表示50岁以上的人的年龄，由计算可知：
μ老年人（55）=0.5
这表示55岁的人只能算“半老”，因为他属于老年人集合的隶属度为0.5。60岁的人的隶属度为0.8。65岁的为0.9。70岁的为0.91。80岁的为0.97。90岁的为0.98，等等8.8黄金分割与斐波那契数列兔子繁殖问题与“斐波那契数列”
{Fn}:1，1，2，3，5，8，13，…（n=0，1，2…）
该数列的通项公式斐波那契数列和贾宪三角形（斐波那契数列的应用）斐波那契数列与植物形态的联系8.9编码技术与密钥体制
数论：古老的学科，“清白的”分枝，巨大的应用威力仙农—信息论的创始人
一种可以发现错误并能改正错误的编码方案—奇偶校验码，是一种可以发现错误并改正错误的编码方案，又称（7，4）码。公开密钥体