地月转移轨道特征及快速设计方法.pdf

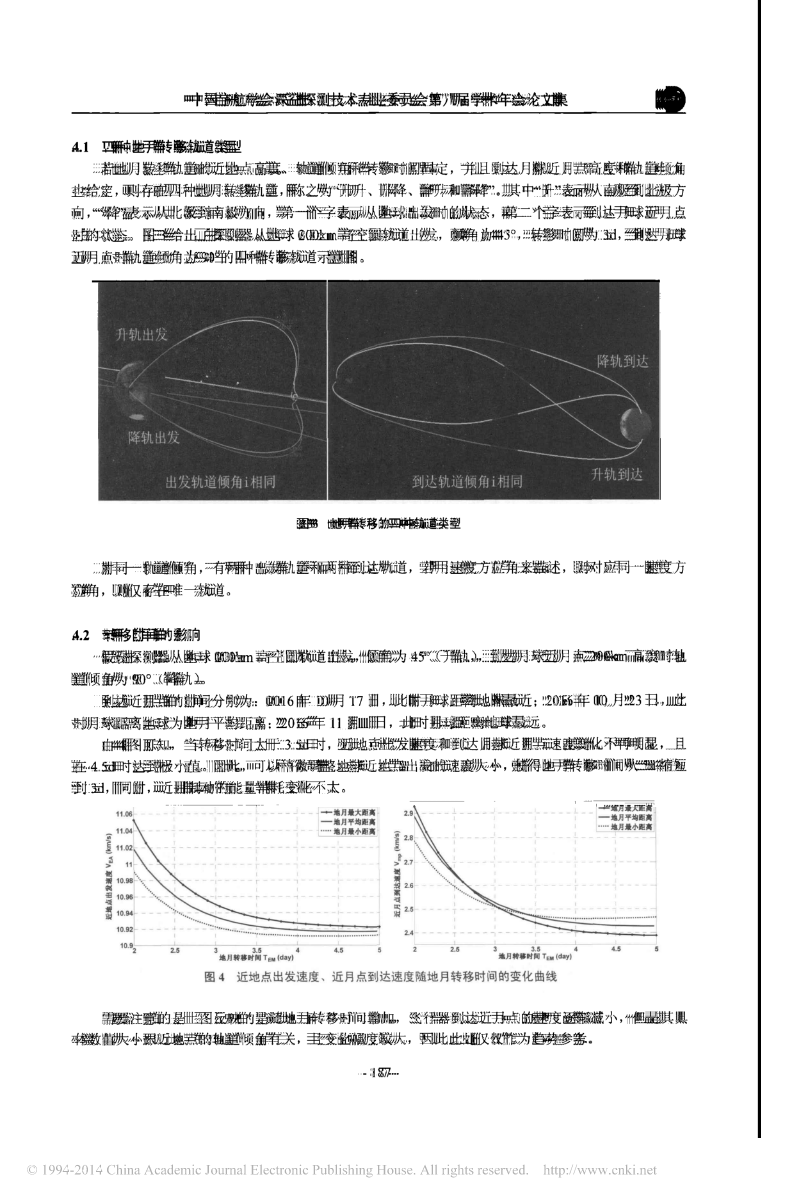
中国宇航学会深空探测技术专业委员会第八届学术年会论文集

地月转移轨道特征及快速设计方法

,
李云飞,2

..
(1上海市空间飞行器机构重点实验室;2上海宇航系统工程研究所)

。,
摘要:针对地月直接转移轨道进行分析首先提出双二体简化模型在此模型下直接给出地月

,
转移轨道的一些重要特征;其次给出了地月转移转轨道的数值设计方法,根据此算法可以很快的求

,,
解出精确的地月转移轨道;最后利用完整力模型,给出了地月转移轨道的一些重要特征验证了双
二体简化模型的正确性。
关键词:地月转移轨道;轨道特征;轨道设计;数值计算

1引言

,,,
月球探测器在地月空间运动时同时受到地球和月球的引力这是一个典型的三体问题其运动

。,,,
方程至今没有完整的解析解近地空间初始速度不同其运行轨道也大不一样总的来说地月转移
轨道可分为以下三种:

。,,
第一种是直接转移型在近地轨道和运载火箭分离后探测器获得一个比较大的初速度以大偏

,,
心率椭圆的轨道形式经过3一d5左右的时间即可到达月球附近这是目前世界上绝大多数月球探测器

,。,,
所采用的转移方式我国的探月工程也采用此方式此种方式的转移时间短工程实施难度较低对

,。
于现有运载火箭能力而言完全可以保证近地点处附近较大的初速度
第二种是低能转移型。即利用日、地、月平动点轨道特征进行的低能量转移,通常将探测器射入

一,,
地月系的Ll点附近然后施加小的速度增量使探测器从Ll点飞向月球形成绕月轨道;另一种方式

一,,一
是将探测器发射到日地系的LZ点附近经过变轨后再利用地月系LZ点的稳定流形使得探测器“自

。,
动”的运行到近月空间附近(也称弱稳定边界转移轨道)从理论上讲采用低能转移型的地月转移轨
道所需的速度增量都较直接转移型小,但是,低能转移轨道都是弱稳定的,对误差非常敏感,这给探

。
测器的控制带来非常大的难度而所带来的速度增量的节省(百米每秒左右)对于工程实施来讲优势并不
明显,同时地月转移时间大大增加。所以,这种轨道很少在工程中使用,常作急救方案加以研究。
第三种是小推力转移型。这种转移轨道通常适用带离子推进的探测器。初始加速段轨迹通常为向
外的螺旋式轨道;当探测器进入月球影响球后,再逐渐减速直到达到给定的环月轨道。这种类型的转

,,
移轨道所需的飞行时间较长从几个月到十几个月目前仅有欧空局“SMART-1”月球探测器实现这
种转移方式。
本文仅对第一种直接转移型的轨道进行研究。

2双二体简化模型
由于月球质量远远小于地球质量,因此月球探测器在地月空间运动时其轨道有着明显的特点。在
地球附近时,地球引力起主导作用,探测器与地球构成二体系统;在月球附近时,月球引力起主导作

,。,
用此时探测器与月球构成一个二体系统按照拉普拉斯(L叩lace)对引力范围的定义月球的影响

,,,
球半径约为.66万公里因此在地月转移过程中探测器大部分时间是在地球引力范围内的大椭圆运动
到达月球附近时,相对月球作双曲线运动。

183
中国宇航学会深空探测技术专业委员会第八届学术年会论文集

,
常采用双二体模型进行地月转移轨道的设计它将地月转移轨道分为两部分:近地段轨道和近月

。,,
段轨道近地段是以地球为引力中心的椭圆轨道近月段是以月球为引力中心的双曲轨道两个轨道

,、。
在月球影响球处拼接即位置速度在拼接点处相同尽管双二体模型从理论上能够较精确的描述地

,,。
月转移轨道但在轨道拼接过程中涉及到复杂的公式计算且无法获得直观的结论

,,,
本文对双二体模型进行简化并直接给出地月转移轨道的一些特征在此基础上给出简单的数

。
值计算方法双二体简化模型定义如下:

,.,.
(l)地球为圆球体半径天广6378137咖地球引力常数所3986005枷,25,;
,.,
(2)月球绕地球作均匀圆周运动地月距离R犷3840mk;月球引力常数闪厂4902803腼5/2
月球半径R厂1738kni;
,,,,
(3)地月转移轨道忽略月球的影响球大小仅考虑地球中心引力作用为二体轨道其轨道始
末两点分别为地球中心和月球中心;且在月心处相对月心的速度为代;

,,,
(4)月球影响球内的轨道仅考虑月球中心引力场作用为双曲轨道其无穷远处速度矢量为`in;

。
(5)氏=v二in

.21地月转移轨道

,。
对于从地球上发射的月球探测器来说运载火箭通常将探测器送入20kni高度的地月转移轨道
.,。
因此地月转移轨道的近地点RAE=6578137玩设其近地点处速度大小为AEv
,,,
由二体轨道可知最简单的地月转移轨道为霍曼转移轨道远地点就是地月距离其近地点速度

,
也是地月转移轨道所需的最小速度其值如下:

.
=loglsmk/s(l)

。,
对应此霍曼转移轨