月球卫星轨道设计优化_林胜勇.pdf

..
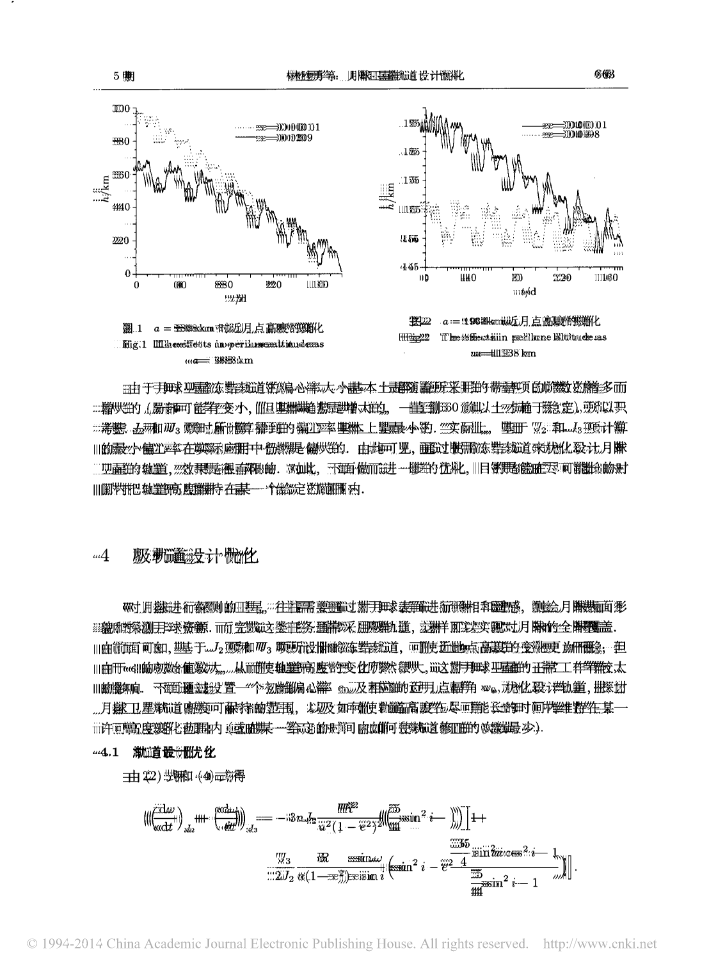
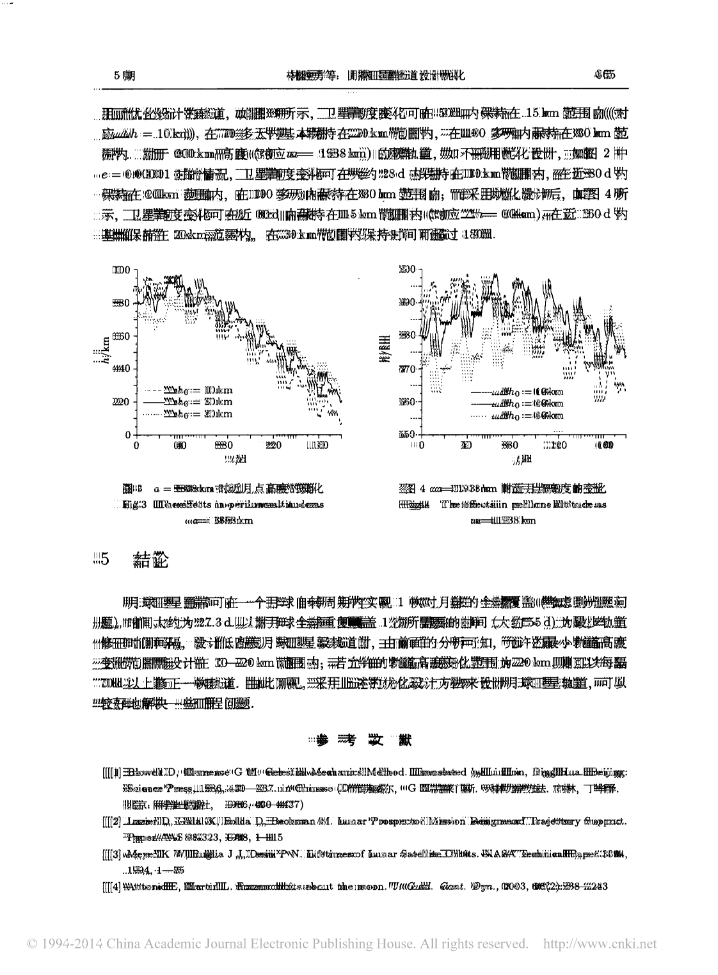
第24卷第5期空间科学学报V乙124,No5

,
2004年9月CHINESEJOURNALOFSPACESCIENCESePt,2004

月球卫星轨道设计优化

,
林胜勇‘2李珠基2和兴锁
(西北工业大学工程力学系西安710072)
(上海宇航系统工程研究所)

摘要

.
利用带谐项几和Js对月球卫星轨道进行了优化设计首先分析了月球卫星轨道摄动因
素对轨道的影响,其次推导了对应于几和几项的冻结轨道计算公式,并通过对仅包含月球

.
引力场模型的运动微分方程,直接积分计算轨道的变化进行了验证最后,通过合理选择初
始轨道的偏心率e。和近月点幅角。。,对月球卫星极轨道进行了优化设计,给出了设计公式

..
并进行了仿真结果表明,这种优化设计方法是很有效的
关键词月球卫星;摄动;冻结轨道;轨道设计;优化

1引言

.
月球周围没有大气,因此理论上月球卫星可以在尽可能低的轨道上工作但是实践表
明,在月球非球形引力、地球和太阳引力以及太阳光压等的作用下,月球卫星轨道有较大

.,
的摄动第一颗人造月球卫星“月球10号”其初始轨道为近月点高度350km,远月点高

,.,.,
度1017km,两个月后轨道参数变为近月点高度3787km远月点高度9853km轨道明

.
显变圆了,即偏心率变小了[lJ相反,如果在一段时间内偏心率不断地增大,将使月球卫

,
星的近月点高度降低;而如果近月点高度降得很低的话,就有可能使卫星撞毁在月面上

,
根据预测美国的“月球勘探者”探测器(高度为lokm的极圆轨道)如果不进行轨道维

,.,,
持大约150d内即撞上月球[a]另外月球卫星轨道高度的剧烈变化对星上有效载荷

.,,
的正常工作(如照相等)也有较大的影响因此对月球卫星轨道进行优化设计使轨道
高度变化较平稳,不但可以减少轨道修正次数和燃料消耗,还可以保证月球卫星的正常工

.
作

、、、
文献同采用5xs阶次月球引力场模型的子集(包括了5个引力参数几Ja几

,.
汤2和几1)研究了低高度月球卫星轨道的寿命以确定月球使命中可使用的停泊轨道

,“
文献[]’和[sl则通过使用冻结轨道来优化设计月球卫星轨道其中文献!5」中为月球勘
探者”探测器设计的准冻结轨道可使轨道修正的时间间隔达到2个恒星月(、5d),轨道

.
高度的变化范围维持在士20km之内

、
本文将通过合理设计月球卫星轨道的偏心率近月点幅角和轨道倾角(通常轨道倾角

,
是根据任务已设计好的)之间的关系使轨道高度变化在尽可能长的时间内维持在某一给

.
定的范围内

一一
20031203收到原稿,20今07-12收到修定稿
:
5期林胜勇等月球卫星轨道设计优化361

2轨道摄动分析

与人造地球卫星的相似,月球卫星的力学模型对应的仍是一个受摄二体问题,原则上

.
用于求解人造地球卫星运动方程的各种方法都可用于求解月球卫星运动方程与地球卫

.
星相比,月球卫星所处的力学环境主要有以下不同[6]

,,.
(l)月球为一慢自转天体其自转的周期与绕地球公转的周期相等都是273个平太

.
阳日这样对于月球引力的非球形带谐项,其相对于地球引力的相应的摄动项,就可能由

.
短周期项转变为长周期项

,.,
(2)相比于地球非球形引力月球非球形引力位的各系数的量级比较接近例如月
球的2、3阶带谐项几和几仅相差1个量级多一点,而地球的几和Ja项则相差近3个

.
量级

,,
(3)月球表面没有大气因而其轨道运动没有相应的能量损耗运动方程的求解也更

.
简单一些

,
(4)相对于月球和太阳对人造地球卫星的影响因月球的质量远小于地球和太阳的质

.
量,因而地球和太阳对月球卫星的影响相对更大一些
对于低高度月球卫星轨道,其主要摄动是月球的非球形摄动,尽管地球引力和太阳引
力等摄动对月球卫星轨道也有一定的影响,但是它们与月球的非球形摄动相比还是很小

.、
的文献闭计算了20km高度的圆轨极月卫星lo31h内分别在地球引力摄动月球非球

、.,、
形摄动太阳引力摄动和光压摄动作用下其卫星轨道的变化结果表明(l)长半轴升

,,
交点经度和轨道倾角的变化很小基本上可以忽略不计而偏心率则有较大的变化;(2)
月球非球形摄动在偏心率的变化中占主导地位,而地球引力、太阳引力和光压等摄动对其

.
影响则相对小得多

.
因此本文仅就月球引力场作用下的低高度月球卫星轨道进行优化设计

3冻结轨道设计

冻结轨道实际上是各阶带谐项平衡的结果,即偶次带谐项引起的近地点幅角。的长

.
期摄动被奇次带谐项引起的长期摄动所平衡[s]因此,冻结轨道偏心率的计算精度取决于

.
所采用的带谐场的大小,带谐项取得越多,精度越高,但计算的工作量也随之增大下面

.
分