汽车转向梯形机构的优化设计.pdf

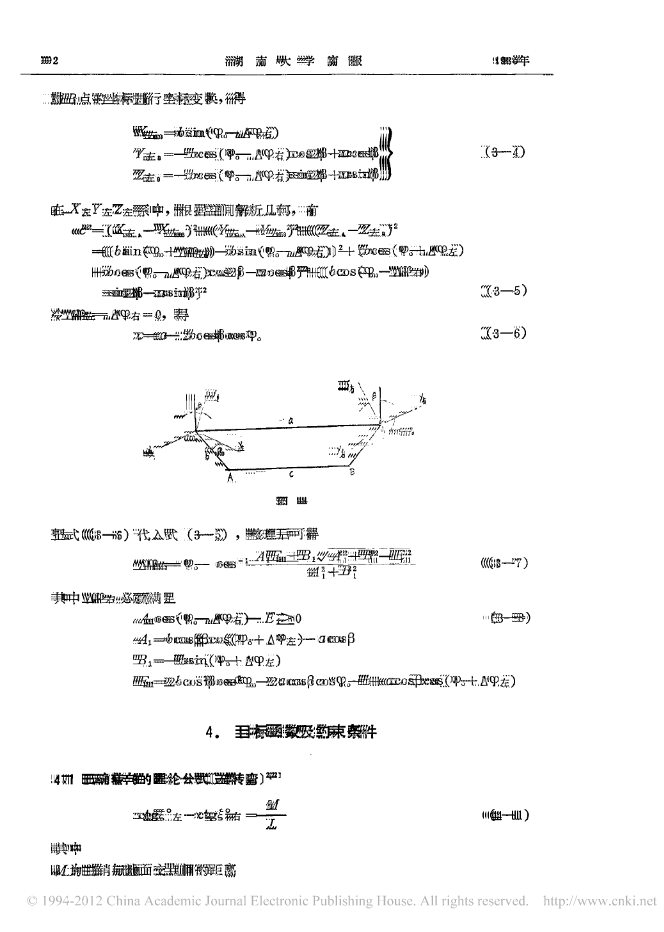
湖南大学学才皮

.,.,
第12卷第4期JOURNALOFHUNA凡UNIVERSITYVoiiZNo41985

汽车转向梯形机构的优化设计
林金木李宜芳

(机械工程系)

I摘要】本文提出设计汽车转向梯形的数学模型,模型中考虑了主销
后倾角,车轮外倾角及主销内倾角在转向时的作用。计算结果表明,优化
后的机构参数更为合理。

.
1前言

、
汽车转向时,内外轮的转角要维持某种关系,这个通常由梯形机构来实现。以前
梯形机构的设计,一般都把它简化为平面机构,用分析法或作图法确定机构的参数。实
际上,车轮存在主销后倾角,主销内倾角和车轮外倾角,梯形机构是空间机构。显然,
这样的设计方法精度较差,不可能对参数进行优选,有进一步改善的余地。本文考虑了
前轮定位角的影响,提出设计梯形机构的数学模型,并且对参数进行优化。计算表明,
优化后的机构参数更为合理。

.
2转向节绕主销转角与车轮转角

.
2飞左前轮(顺着汽车前进方向)

在图l中,丫为主销后倾角,日为主销内倾角,e为主锁轴线与铅直线的夹角。球
面ab‘的球心为O点,平面aoC土平面b口c,平面aoC与boa之间两面角为入。
在球面△abc中

山
eoso一eooyeoop+sinysin日eosgo“。

一·
O=eos’(eooyeosp)(2一1)御肠ˆ
sin入singo。
sinpsino
_,1oin日\
‘~22
A二出n一叮二二产j(一)
、吕InU,
在图2中,Oa为铅直线,Ob为主销轴线,△甲左为转向

本文于1984年2月15日收到
湖南大学学报1955年

节绕主销转角;OA为直线行驶时车轮轴线,OB为绕主销转△甲左后的车轮轴线;a为
车轮外倾角,,a为绕主销转△甲左后的车轮外倾角,省左为对应于绕主销转△甲左后的车
轮转角;E为bA与bB弧对应的球心角;ABab为球面,球心在O点。

协‘

咬、
厂六曰
田2

在球面△Aab中

。。“
coSE二cosocos(90+a)+sinosin(90+a)eos(90+入)

一‘
E二eos(eososi及a+sinoeosasin入)(2一3)
“in△~sin(900+入)
“
sin(90+a)sinE

△一“‘n一‘三互
望琴婴、(2一4)
(吕In乙/
在球面△B月b中
cos乙二co“zE+sinZEeos△甲左(z一5)
在球面△Bab中
eo,(90“+a尹)=eosEeo80+sinEsinoeos(△甲左一△)

一’
a,=sin(一eosEeooo一sinEsinoeos(△rp左一△))(2一6)
在球面△AaB中

”‘““‘“
eos乙~eo。(90+a)eo。(90+a)+sin(90+a)sin(90+a)eo。占左

.;:左-COS一eos乙一sina产sina
27
,(一)
(eo吕仅eosa)

2.2右前轮

右前轮的绕主销转角与车轮转角的关系与左前轮相似,见图3。其中,△甲右为右
转向节绕主销转角,占右为车轮转角。

产厅
:右一c。。一eos乙一sinasina
28
,’一
(eos仪eosa()

eos产eo吕ZsnZeos右
己二E+iE△甲(2一9)
“s一’coocosseos
a~in(一Eoo一inEino(△甲右+△))(2一10)
其余符号意义同前。
第4期林金木等:汽车转向梯形机构的优化设计

图8

3.坐标变换与几何关系

在图4中,OABO:为梯形机构,00:=a,AB一c,月O和BO,的真实长度为b;

、
AO工OZ左,BO;上012右;02左和O:Z右分别为左右轮的主销轴线。
X左Y左z左和X右Y右Z右为两个空间坐标系,它们的关系为
{X}左=A{X}右+B(3一z)
其中

、.l尹10
ew
eosZ_ssnZ
A一日日

sinZ日eosZ日

B=(0aeos日asin日〕T
{X}右=〔X右Y右Z右〕T{X蛋左=〔X左Y左Z左〕T

。。。
设AO与Oy左的夹角为甲,则BO:与01犷右的夹角为兀一甲当AO绕主销转
动△甲左时,BO:绕主销的对应转角为△甲右。则有
A点的坐标为

。
X左人=bsin(甲+△甲左)

。
Y左‘=bcos(甲+△甲左)(3一2)
Z左‘=O}
B点的坐标为

。
X右:一bsin(CP一△甲右)

。。
Y右=一bcos(甲一△甲右)(3一3)
Z右。~O}
92湖南大学南报1985年

对B点的坐标进行坐标变换,得

。。
X左一bsin(甲一△甲右)

。
犷左。二一beos(甲一A甲右)eosZ日+aeos日(3一4)

。
Z左。=一beos(甲一△甲右)sinZp+asiop

在X左y左Z左系中,根据空间解析几何,有

‘