数值积分法仿真.ppt

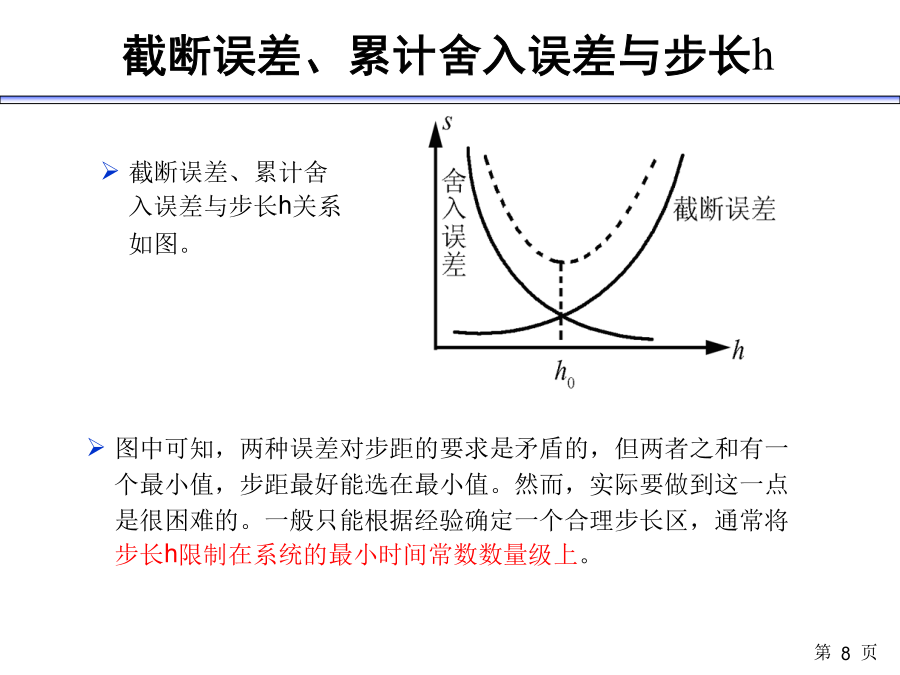
第三章数值积分法仿真Overview第一节数字仿真原理数值积分基本原理步长：
将时间t离散t(k)(k=1,2,…n)，相邻两点的距离为步长，即h=t(k+1)-t(k)
步进法：
数值积分法求近似解根据初始值y0，按照离散的时间序列步进求解。
t0t1t2t3…tn
y0y1y2y3…tn
计算格式：
由y(k)计算出y(k+1)（k=0,1,…,n)的递推公式。数值积分的基本性能计算速度和计算精度截断误差、累计舍入误差与步长h引理：
泰勒级数:如果f(x)在x0点处任意阶可导,则在该邻域内的n阶泰勒公式为：2.1一阶欧拉法一阶欧拉法图示2.22阶龙格-库塔2阶龙格-库塔2阶龙格-库塔2阶龙格-库塔2阶龙格-库塔图示比较高阶龙格-库塔(RK-4)高阶龙格-库塔(RK-4)单步法的特点第三节变步长龙格-库塔法3.1误差估计Runge-Kutta-Fehlberg(RK45)Runge-Kutta-Fehlberg(RK45)RKF-12RKS-34（1978，Shamping）3.2步长控制步长控制：加倍-减半法步长控制：最优步长法1.2.2步长控制龙格-库塔方法的一般形式第三节线性多步法线性多步法原理3.1预报公式3.1预报公式3.1预报公式预报举例3.2校正公式3.2校正公式3.2校正公式预报-校正举例预报-校正举例3.3Adams公式显式Adams系数隐式Adams系数3.4多步法的特点第四节积分算法的稳定性4.1一阶Adams法的稳定性分析一阶Adams法的稳定性分析4.2一般算法的稳定性分析主要算法的稳定性第五节Matlab实现微分方程模型描述数值积分算法描述数值积分算法描述数值积分算法描述微分方程模型描述ode45ode45ode45ode45ode45其他算法简介