
《资本资产定价模型》.ppt

15****92


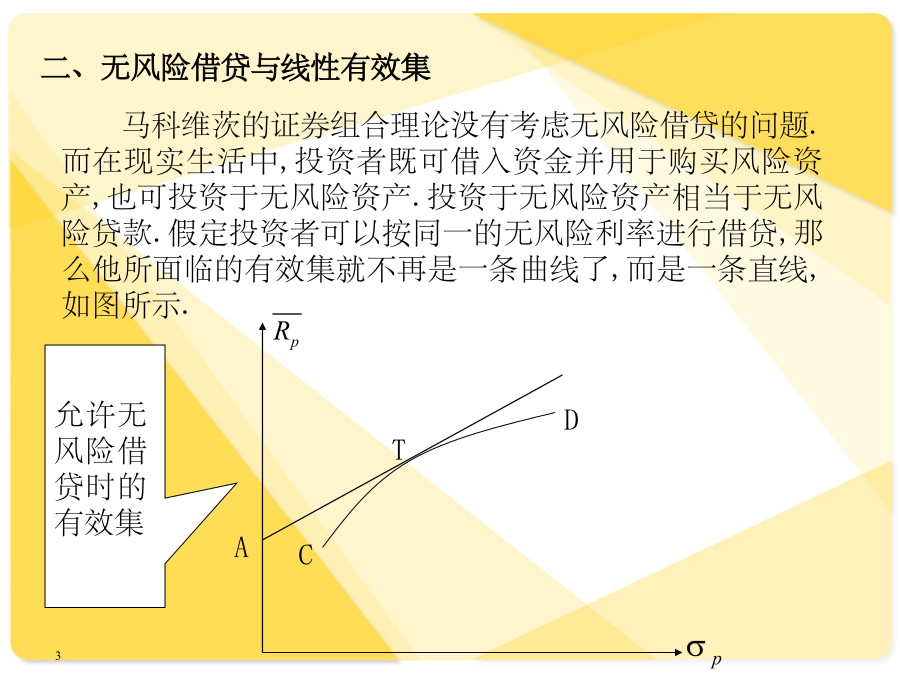

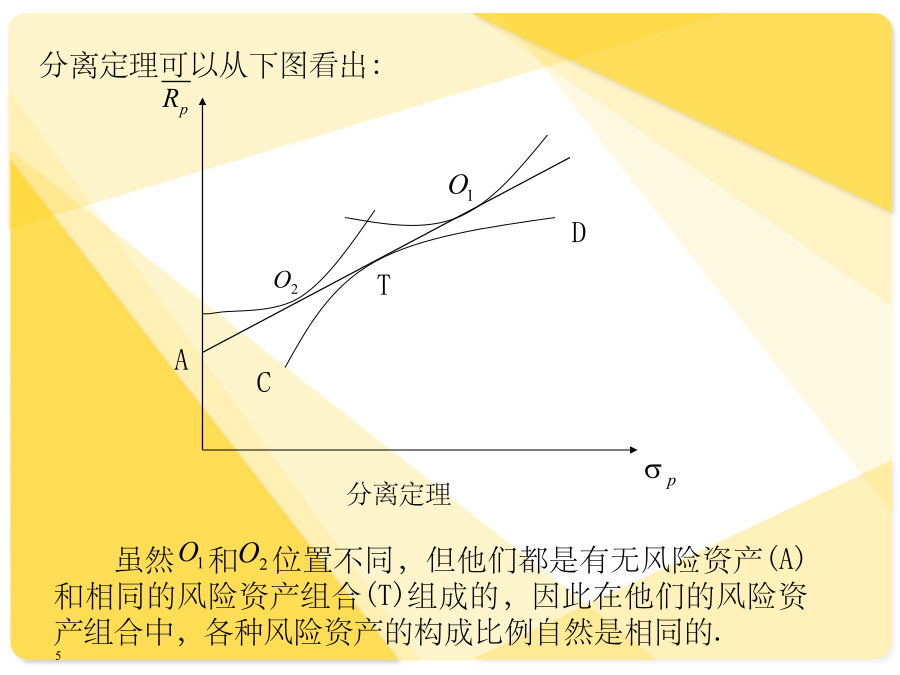



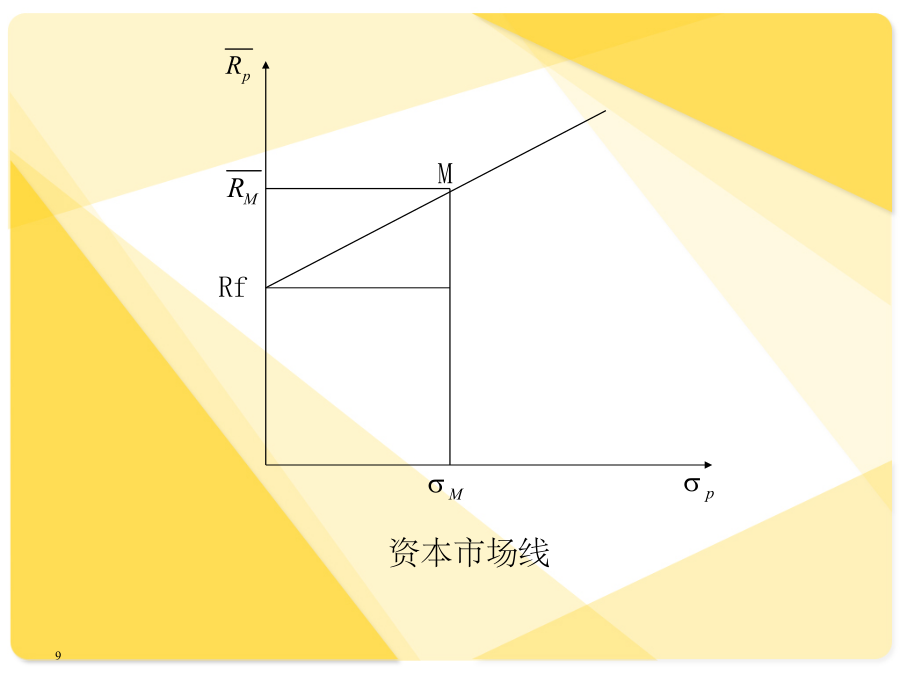

亲,该文档总共24页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

风险资产的定价——资本资产定价模型.ppt
风险资产的定价-资本资产定价模型本章主要问题本章重点内容第一节无风险借贷及其对投资组合有效集的影响第二节标准的资本资产定价模型--资本市场均衡及均衡时证券风险与收益的关系第三节特征线模型--证券收益率与均衡时市场收益率的关系、阿尔发系数第四节资本资产定价模型的检验与扩展第一节无风险借贷对有马科维兹有效集的影响一、无风险资产的定义根据定义无风险资产具有确定的回报率,因此:首先,无风险资产必定是某种具有固定收益,并且没有任何违约的可能的证券。其次,无风险资产应当没有市场风险。二、允许无风险贷款下的投资组合考虑

风险资产的定价-资本资产定价模型.ppt
风险资产的定价-资本资产定价模型本章主要问题本章重点内容第一节无风险借贷及其对投资组合有效集的影响第二节标准的资本资产定价模型--资本市场均衡及均衡时证券风险与收益的关系第三节特征线模型--证券收益率与均衡时市场收益率的关系、阿尔发系数第四节资本资产定价模型的检验与扩展第一节无风险借贷对有马科维兹有效集的影响一、无风险资产的定义根据定义无风险资产具有确定的回报率,因此:首先,无风险资产必定是某种具有固定收益,并且没有任何违约的可能的证券。其次,无风险资产应当没有市场风险。二、允许无风险贷款下的投资组合考虑

风险资产的定价——资本资产定价模型.pptx
风险资产的定价-资本资产定价模型本章主要问题本章重点内容第一节无风险借贷及其对投资组合有效集的影响第二节标准的资本资产定价模型--资本市场均衡及均衡时证券风险与收益的关系第三节特征线模型--证券收益率与均衡时市场收益率的关系、阿尔发系数第四节资本资产定价模型的检验与扩展第一节无风险借贷对有马科维兹有效集的影响一、无风险资产的定义根据定义无风险资产具有确定的回报率,因此:首先,无风险资产必定是某种具有固定收益,并且没有任何违约的可能的证券。其次,无风险资产应当没有市场风险。二、允许无风险贷款下的投资组合考虑

资本资产定价模型.ppt
威廉·夏普(1934—),1990年诺贝尔经济学奖获得者。夏普对经济学的主要贡献是在有价证券理论方面对不确定条件下金融决策的规范分析,以及资本市场理论方面关于以不确定性为特征的金融市场的实证性均衡理论。资本资产定价模型,CAPM模型:CAPM表明一项特定资产的期望报酬率取决于:货币的时间价值。通过测度,是货币在不承担任何风险的回报;承担系统风险的回报。通过市场风险报酬测度;不可分散风险的大小。通过测度,是一项特定资产相对于平均资产所面临的不可分散风险的大小例:某公司股票的贝塔系数为1.4,无风险利率为9%

资本资产定价模型.ppt
CapitalassetpricingmodelCapitalAssetPricingModel(CAPM)CAPM模型是资本市场均衡模型TopicsCovered10.1简单形式CAPM的假设10.1Assumptions(cont’d)7、Single-periodinvestmenthorizon.8、9、Informationiscostlessandavailabletoallinvestors.10、Therearehomogeneousexpectations.*11、投资范围仅限于公开金融
