第四章 系统模型与模型化技术(参考).ppt

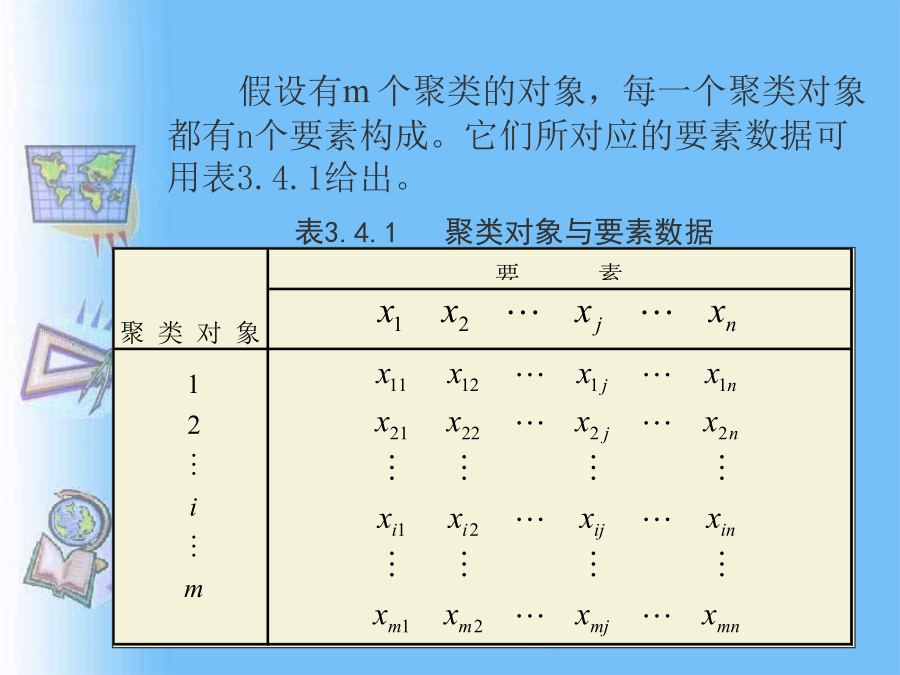
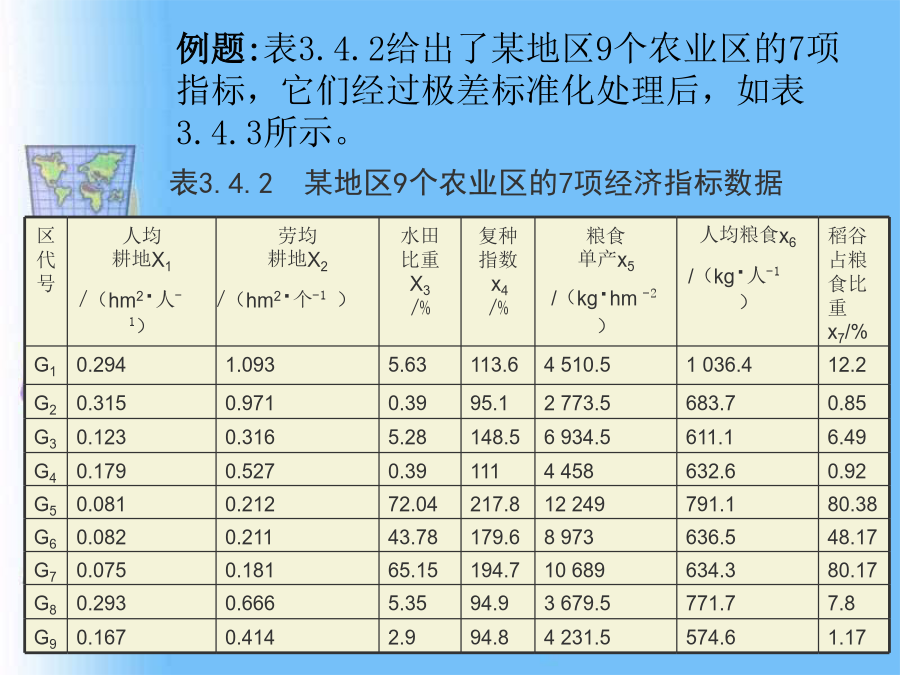
第4节系统聚类分析一、聚类要素的数据处理假设有m个聚类的对象，每一个聚类对象都有n个要素构成。它们所对应的要素数据可用表3.4.1给出。在聚类分析中，常用的聚类要素的数据处理方法有如下几种:②标准差标准化，即

由这种标准化方法所得到的新数据，各要素的平均值为0，标准差为1，即有

③极大值标准化，即

经过这种标准化所得的新数据，各要素的极大值为1，其余各数值小于1。
④极差的标准化，即

经过这种标准化所得的新数据，各要素的极大值为1，极小值为0，其余的数值均在0与1之间。例题:表3.4.2给出了某地区9个农业区的7项指标，它们经过极差标准化处理后，如表3.4.3所示。表3.4.3极差标准化处理后的数据二、距离的计算④切比雪夫距离。当明科夫斯基距时，有

据表3.4.3中的数据，用公式（3.4.5）式计算可得9个农业区之间的绝对值距离矩阵如下三、直接聚类法例题：根据距离矩阵式（3.4.9），用直接聚类法对某地区的9个农业区进行聚类分析,步骤如下:
(1)在距离矩阵D中，除去对角线元素以外，d49=d94=0.51为最小者，故将第4区与第9区并为一类，划去第9行和第9列；
(2)在余下的元素中，除对角线元素以外，d75=d57=0.83为最小者，故将第5区与第7区并为一类，划掉第7行和第7列；(3)在第2步之后余下的元素之中，除对角线元素以外，d82=d28=0.88为最小者，故将第2区与第8区并为一类，划去第8行和第8列；
(5)在第4步之后余下的元素中，除对角线元素以外，d21=d12=1.52为最小者，故将第1区与第2区并为一类，划去第2行和第2列，此时，第1、2、8区已归并为一类；

(6)在第5步之后余下的元素中，除对角线元素以外，d65=d56=1.78为最小者，故将第5区与第6区并为一类，划去第6行和第6列，此时，第5、6、7区已归并为一类；(7)在第6步之后余下的元素中，除对角线元素以外，d31=d13=3.10为最小者，故将第1区与第3区并为一类，划去第3行和第3列，此时，第1、2、3、4、8、9区已归并为一类；
(8)在第7步之后余下的元素中，除去对角线元素以外，只有d51=d15=5.86，故将第1区与第5区并为一类，划去第5行和第5列，此时，第1、2、3、4、5、6、7、8、9区均归并为一类。
根据上述步骤，可以作出聚类过程的谱系图3.4.1。
图3.4.1直接聚类谱系图四、最短距离聚类法
例题:以下根据式（3.4.9）中的距离矩阵，用最短距离聚类法对某地区的9个农业区进行聚类分析。
(1)在9×9阶距离矩阵D中，非对角元素中最小者是d94=0.51，首先将第4区与第9区并为一类，记为G10=｛G4，G9｝。按照公式（3.4.10）式分别计算G1，G2，G3，G5，G6，G7，G8与G10之间的距离得

d1，10=min｛d14，d19｝=min｛2.19，2.62｝=2.19
d2，10=min｛d24，d29｝=min｛1.47，1.66｝=1.47
d3，10=min｛d34，d39｝=min｛1.23，1.20｝=1.20d5，10=min｛d54，d59｝=min｛4.77，4.84｝=4.77
d6，10=min｛d64，d69｝=min｛2.99，3.06｝=2.99
d7，10=min｛d74，d79｝=min｛4.06，3.32｝=3.32
d8，10=min｛d84，d89｝=min｛1.29，1.40｝=1.29

(2)这样就得到G1，G2，G3，G5，G6，G7，G8，G10上的一个新的8×8阶距离矩阵
(3)在上一步骤中所得到的8×8阶距离矩阵中，非对角元素中最小者为d57=0.83，故将G5与G7归并为一类，记为G11，即G11=｛G5，G7｝。

按照公式（3.4.10）式分别计算G1，G2，G3，G6，G8，G10与G11之间的距离，可得到一个新的7×7阶距离矩阵(4)在第2步所得到的7×7阶距离矩阵中，非对角元素中最小者为d28=0.88，故将G2与G8归并为一类，记为G12，即G12=｛G2，G8｝。再按照公式（3.4.10）分别计算G1，G3，G6，G10，G11与G12之间的距离，可得到一个新的6×6阶距离矩阵(5)在第3步所得的6×6阶距离矩阵中，非对角元素中最小者为d6，11=1.07，故将G6与G11归并为一类，记为G13，即G13=｛G6，G11｝=｛G6，（G5，G7）｝。再按照公式（3.4.10）计算G1，G3，G10，G12与G13之间的距离，可得到一个新的5×5阶距离矩阵(6)在第4步所得的5×5阶距离矩阵中，非对角线元素中最小者为d3，10=1.20，故将G3与G10归并为一类，记为G14，即G14=｛G3，G10｝=｛G3，（G4