龙格库塔方法-PPT.ppt

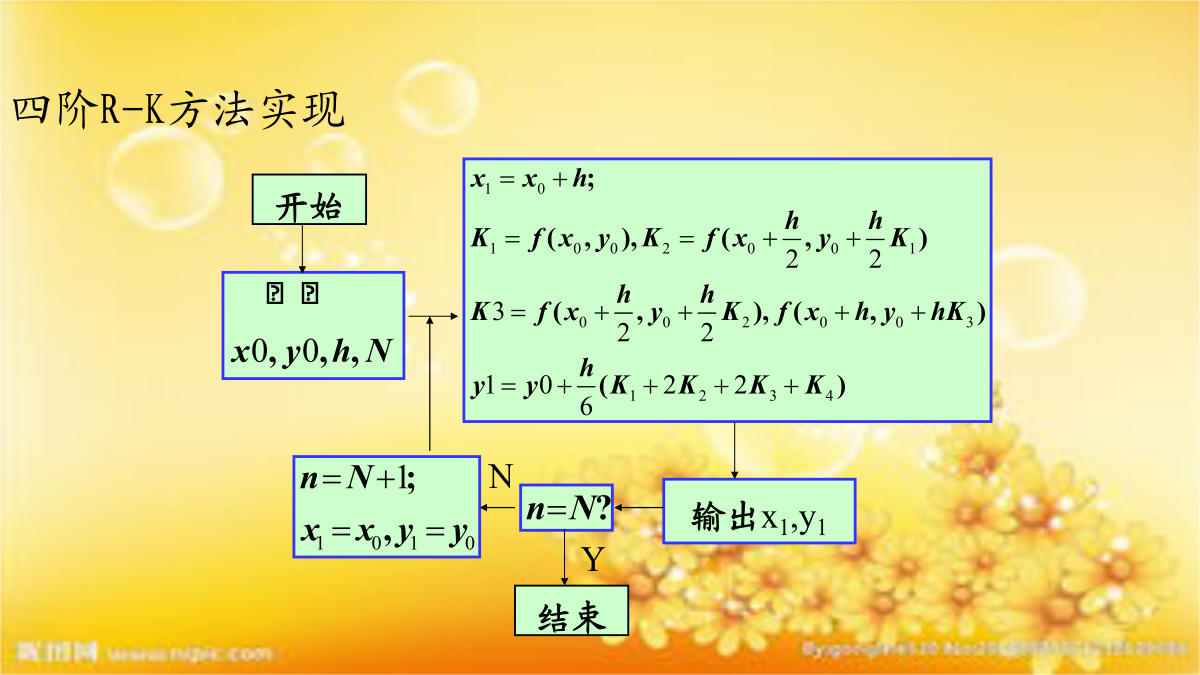
Runge-Kuttua方法和matlab原理龙格－库塔法（Runge-Kutta）
数值分析中，龙格－库塔法（Runge-Kutta）是用于模拟常微分方程的解的重要
的一类隐式或显式迭代法。这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

经典四阶龙格库塔法
龙格库塔法的家族中的一个成员如此常用，以至于经常被称为“RK4”或者就是
“龙格库塔法”。四阶Runge-Kutta方法这样，下一个值(yn+1)由现在的值(yn)加上时间间隔(h)和一个估算的斜率的乘积
决定。该斜率是以下斜率的加权平均：
k1是时间段开始时的斜率；
k2是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn+h/2的值；
k3也是中点的斜率，但是这次采用斜率k2决定y值；
k4是时间段终点的斜率，其y值用k3决定。
当四个斜率取平均时，中点的斜率有更大的权值：误差分析：

注意上述公式对于标量或者向量函数(y可以是向量)都适用。R-K(高阶)方法不唯一,选择不同的参数能得到
不同的R-K公式四阶Runge-Kutta方法的MATLAB实现原理：四阶R-K方法实现functionff=rk(yy,x0,y0,h,a,b)
%yy为y的导函数,x0,y0,为初值,h为步长,a,b为区间
c=(b-a)/h+1;i1=1;
%c为迭代步数；i1为迭代步数累加值
y=y0;z=zeros(c,6);
%z生成c行，6列的零矩阵存放结果；
%每行存放c次迭代结果，每列分别存放k1~k4及y的结果不断迭代运算：
forx=a:h:b

ifi1<=c
k1=feval(yy,x,y);
k2=feval(yy,x+h/2,y+(h*k1)/2);
k3=feval(yy,x+h/2,y+(h*k2)/2);
k4=feval(yy,x+h,y+h*k3);
y=y+(h/6)*(k1+2*k2+2*k3+k4);
z(i1,1)=x;z(i1,2)=k1;z(i1,3)=k2;z(i1,4)=k3;z(i1,5)=k4;z(i1,6)=y;
i1=i1+1;
end
end例4xn改进Euler法一步需要计算两个函数值(h=0.1)
四阶Runge-Kutta方法一步需要计算四个函数值（h=0.2）
总计算量大致相当，但四阶Runge-Kutta方法精度更高五、变步长Runge-Kutta方法实施方案可以通过检查步长折半前后两次计算结果的偏差Thanks！