第7章 应力状态.ppt

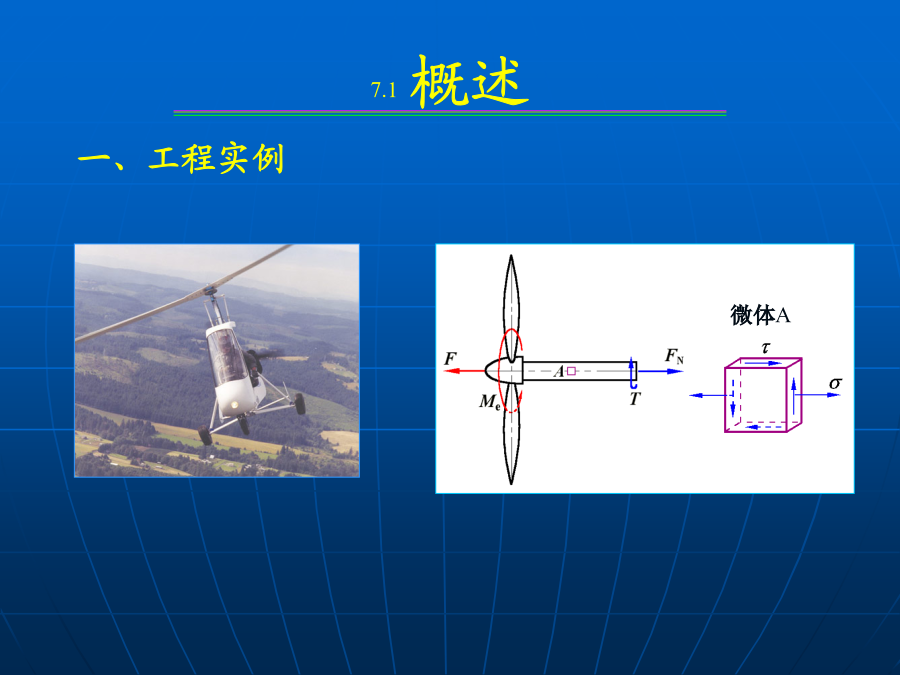
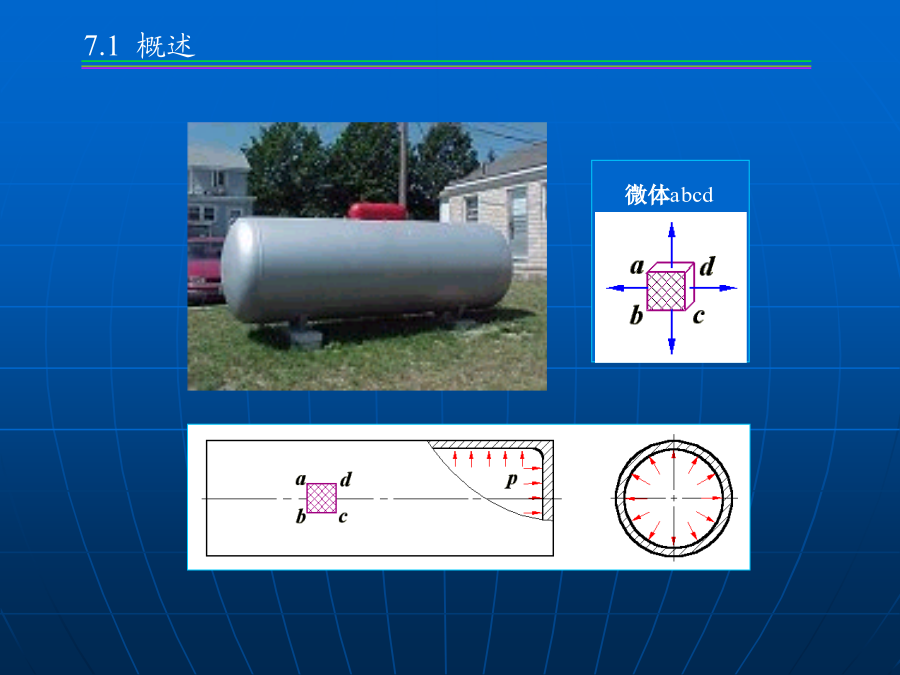
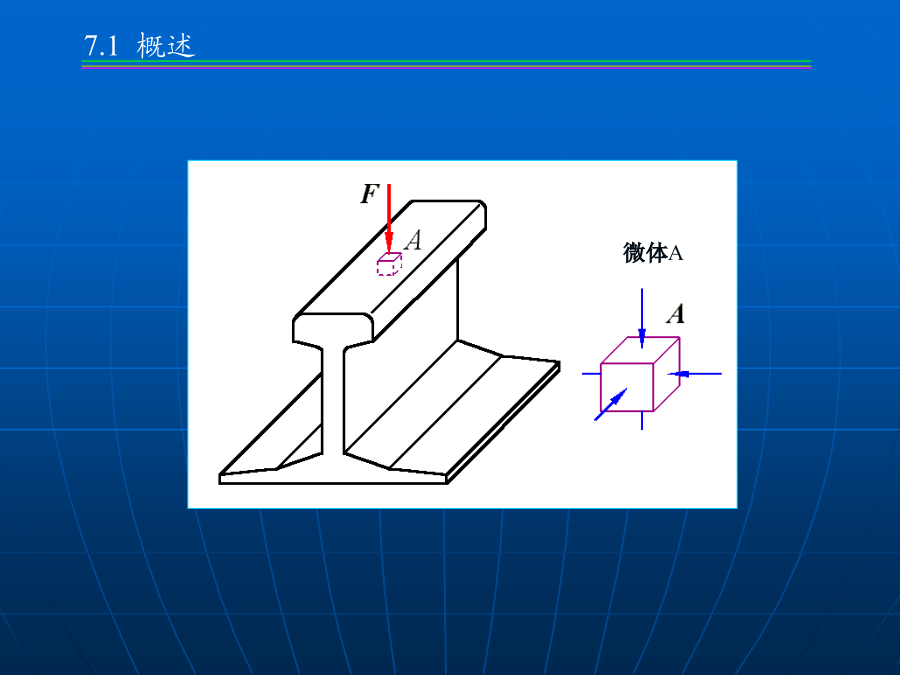
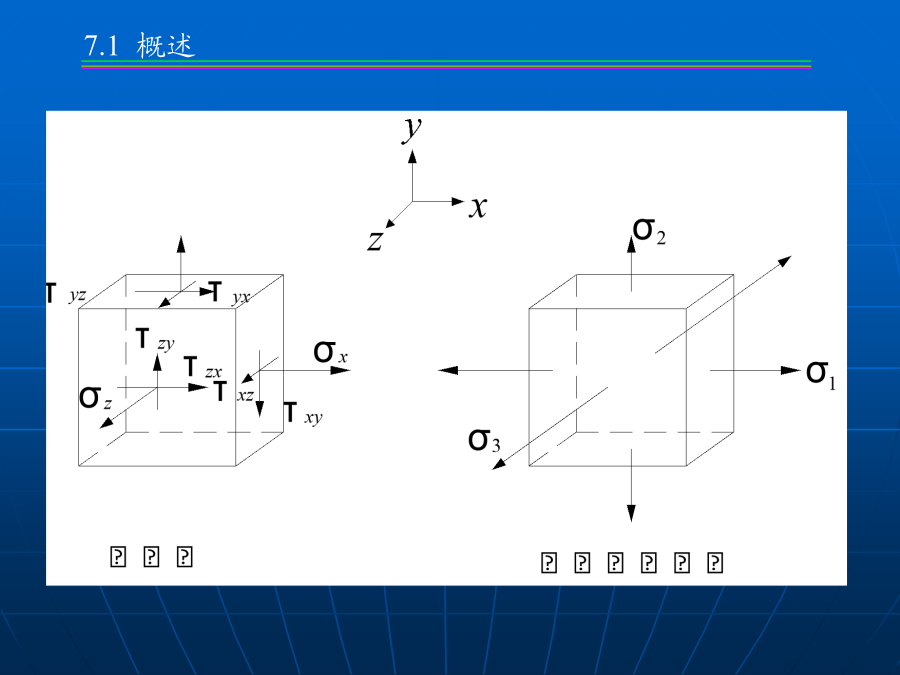
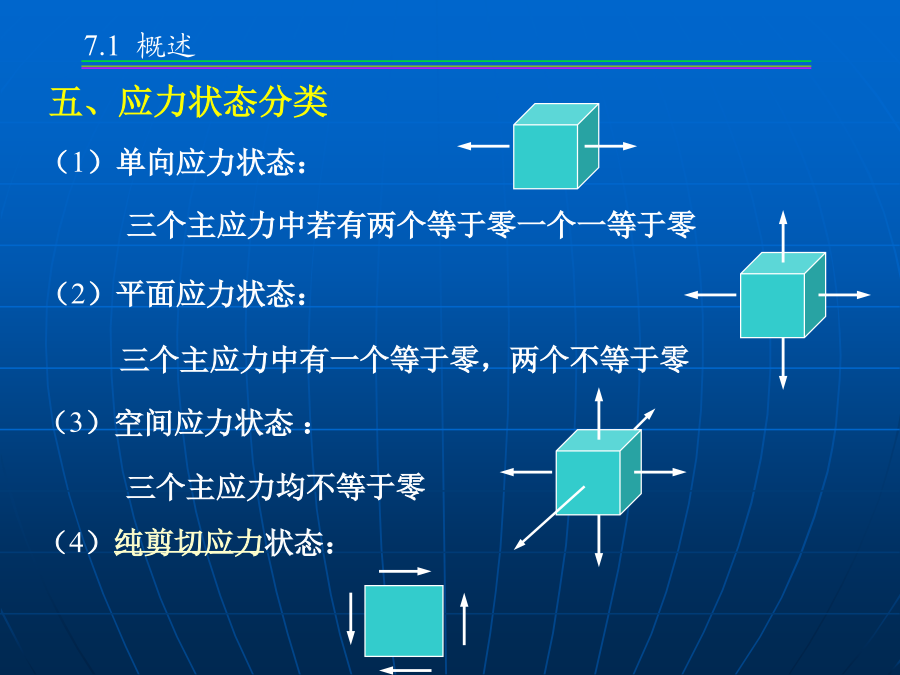
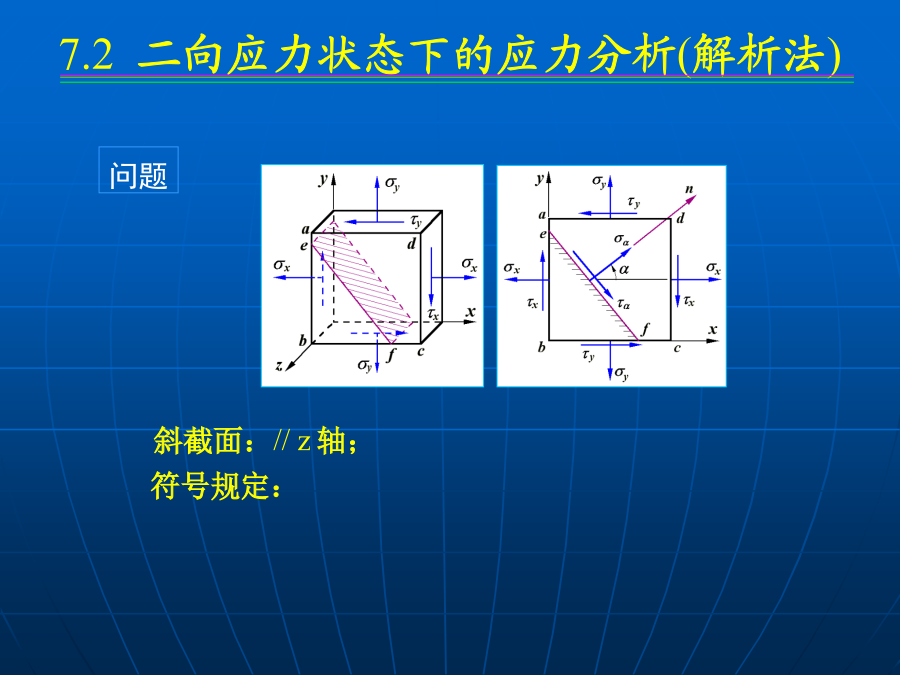
第7章应力状态及应变状态分析第7章应力状态及应变状态分析微体A微体abcd微体A三、受力构件内应力特征：四、单元体法z（2）平面应力状态：问题：建立sa,ta与sx,tx,sy,ty间的关系斜截面应力公式由于tx与ty数值相等,并利用三角函数的变换关系,得例计算截面m-m上的应力主应力:主平面上的正应力称为主应力确定正应力极值由上式可以确定出两个相互垂直的平面，分别为最大正应力和最小正应力所在平面。说明在与同一主平面垂直的所有截面中，任意二互相垂直的截面上的正应力之和为常数。试求（1）斜面上的应力；
（2）主应力、主平面；
（3）绘出主应力单元体。解：（2）主应力、主平面主平面的方位：（3）主单元体：7.2.3比较比较7.2.4二向应力状态的两个特例应力圆应力圆的绘制图解法求斜截面应力点、面对应关系例利用应力圆求截面m-m上的应力极值应力数值极值应力方位主平面－切应力为零的截面应力状态分类纯剪切状态的最大应力圆轴扭转破坏分析解：1.解析法2.图解法23x5将相应的x,x和y=0,y=-x代入主应力的计算公式得梁内任一点的主应力计算公式在梁的xy平面内可以绘制两组正交的曲线。一组
曲线上每一点处切线的方向是该点处主应力1的方向，
而另一组曲线上每一点处切线的方向是该点处主应力
3的方向,这样的曲线称为梁的主应力迹线。上图绘出的是受均布线荷载作用的简支梁的两组主应力迹线实线表示主应力1的迹线,虚线表示主应力3的迹线,所有的迹线与梁轴线(代表梁的中性层位置)间的夹角都是45°,在梁的横截面上=0的各点处,迹线的切线则与梁的轴线平行或正交。7.4梁的应力状态分析及主应力轨迹线与任一截面相对应的点，或位于应力圆上，或位于由应力圆所构成的阴影区域内最大切应力位于与s1及s3均成45的截面上例已知sx=80MPa，tx=35MPa，sy=20MPa，sz=－40MPa，求主应力、最大正应力与最大切应力7.6.1单向应力状态下应力与应变的关系7.6.2纯剪切应力状态下应力与应变的关系（1）符号规定(b)三个剪应力分量:
若正面(外法线与坐标轴
正向一致的平面)上剪应力矢
的指向与坐标轴正向一致,或
负面(外法线与坐标轴负向一
致的平面)上剪应力矢的指向
与坐标轴负向一致，则该剪
应力为正,反之为负。线应变:以伸长为正,
缩短为负。
剪应变:使直角减小者为正,
增大者为负。在xyz分别单独存在时,x方向的线应变x依次为:在xyz同时存在时,x方向的线应变x为公式的适用范围:
在线弹性范围内,小变形条件下,各向同性材料。3、特例
（1）平面应力状态下(假设Z=0)（2）广义胡克定律用主应力和主应变表示时

三向应力状态下：平面应力状态下

设3=0,则7.6.4体积应变体积应变为特例例1已知E=70GPa,m=0.33,求e45。例2对于各向同性材料，试证明：例3边长a=10mm正方形钢块，置槽形刚体内，F=8kN，m=0.3，求钢块的主应力第7章结束