
数据结构-图的基本概念和存储结构.ppt

kp****93






亲,该文档总共63页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数据结构图的基本概念和存储结构.ppt
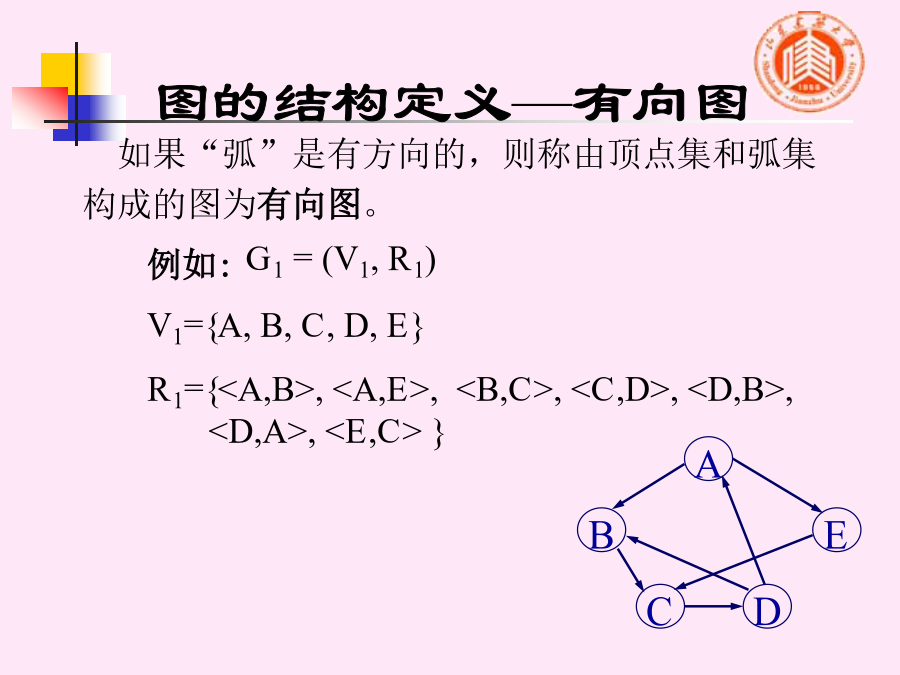
图和图的存储结构图和图的存储结构图的结构定义图的结构定义—有向图图的结构定义—无向图图的结构定义—无向图名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语基本操作基本操作基本操作基本操作基本操作基本操作基本操作一、图的数组(邻接矩阵)存储表示图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接表图的存储表示--邻接表图的

数据结构-图的基本概念和存储结构.ppt
图和图的存储结构图和图的存储结构图的结构定义图的结构定义—有向图图的结构定义—无向图图的结构定义—无向图名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语基本操作基本操作基本操作基本操作基本操作基本操作基本操作一、图的数组(邻接矩阵)存储表示图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接表图的存储表示--邻接表图的

数据结构-图的基本概念和存储结构.ppt
图和图的存储结构图和图的存储结构图的结构定义图的结构定义—有向图图的结构定义—无向图图的结构定义—无向图名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语名词和术语基本操作基本操作基本操作基本操作基本操作基本操作基本操作一、图的数组(邻接矩阵)存储表示图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接矩阵图的存储表示--邻接表图的存储表示--邻接表图的

《数据结构》9.1图的基本概念和存储结构.ppt
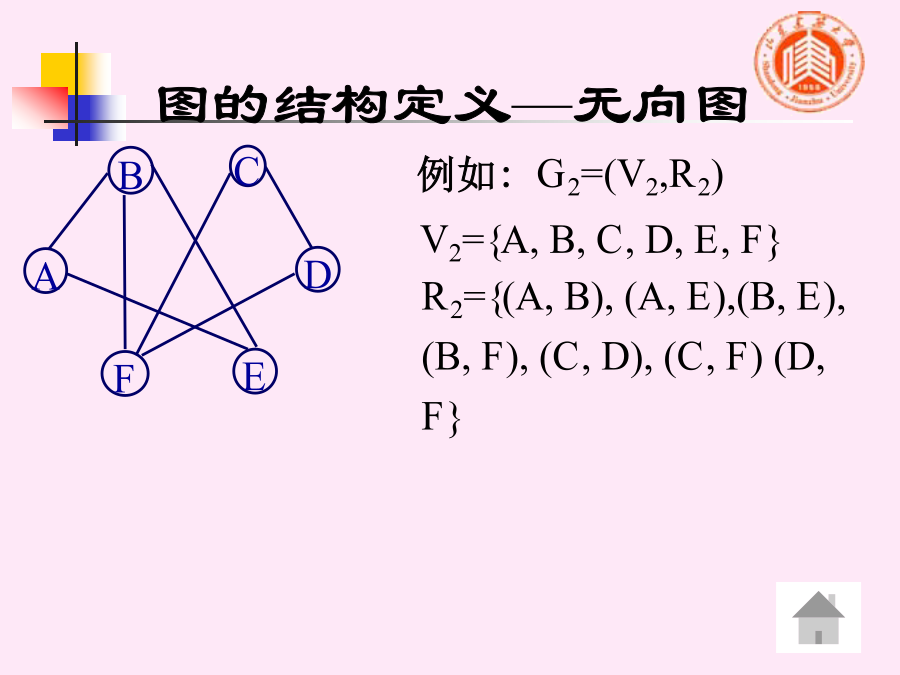
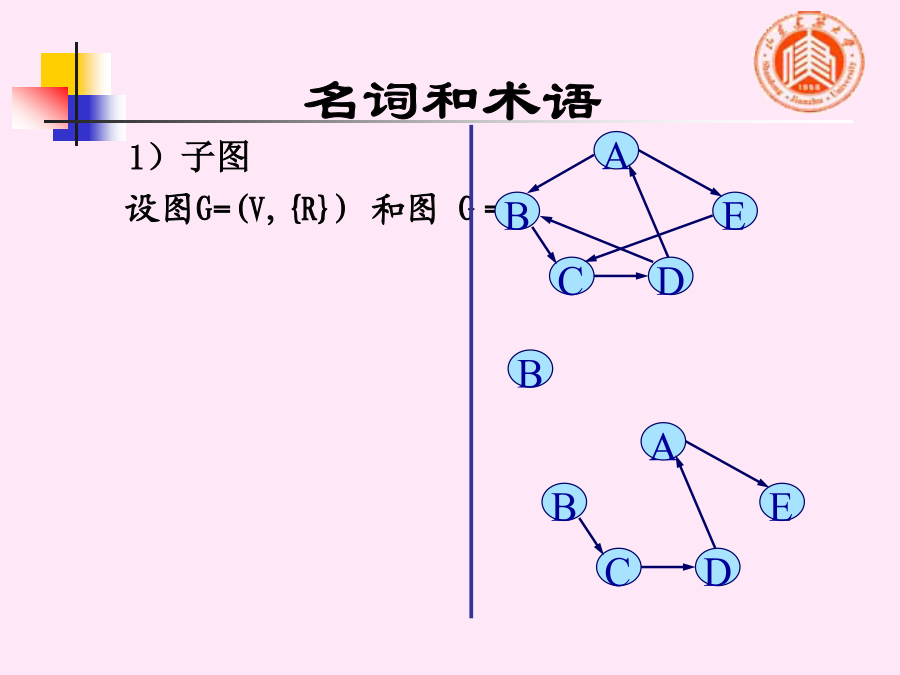
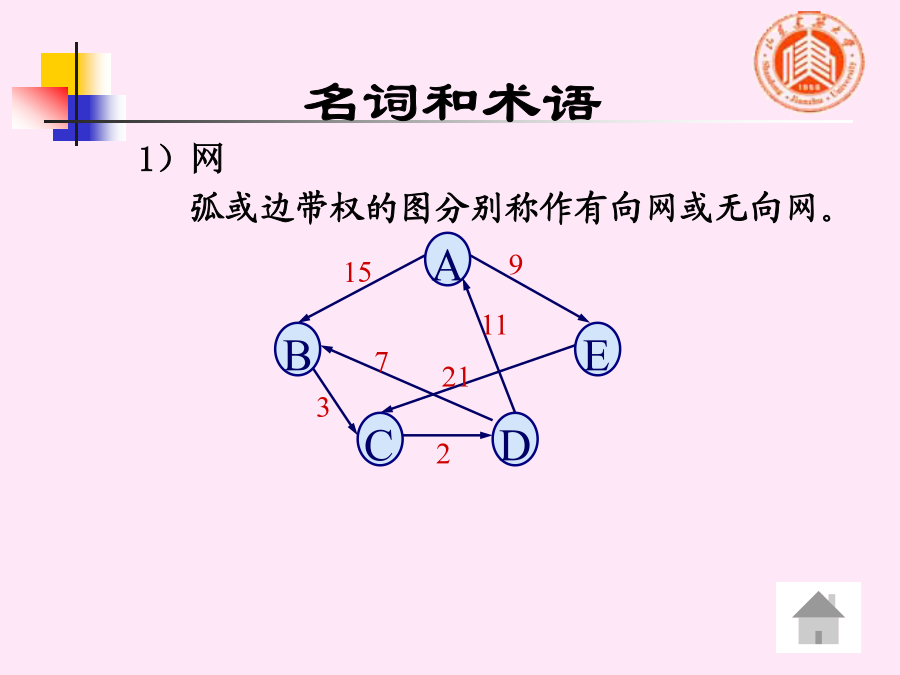
图和图的存储结构1.图的定义图的定义图的定义—有向图图的定义—无向图图的定义—无向图名词和术语1)子图、网弧或边带权的图分别称作有向网或无向网。2)完全图、稀疏图、稠密图3)邻接点、度、入度、出度3)邻接点、度、入度、出度3)邻接点、度、入度、出度3)邻接点、度、入度、出度A简单路径:指序列中顶点不重复出现的路径。5)连通图、强连通图、弱连通图名词和术语强连通图:若有向图任意两个顶点之间都存在一条有向路径,则称为强连通图。基本操作CreatGraph(V,E)://按定义(V,E)构造图2.对顶点的访问操

数据结构图的存储结构及基本操作.docx
实验目的通过上机实验进一步掌握图的存储结构及基本操作的实现。实验内容与要求要求:⑴能根据输入的顶点、边/弧的信息建立图;⑵实现图中顶点、边/弧的插入、删除;⑶实现对该图的深度优先遍历;⑷实现对该图的广度优先遍历。备注:单号基于邻接矩阵,双号基于邻接表存储结构实现上述操作。数据结构设计逻辑结构:图状结构存储结构:顺序存储结构、链式存储结构算法设计#include<stdio.h>#include<string.h>#include<stdlib.h>#defineMAX_VERTEX_NUM20typede
