水平井待钻井眼轨迹最优化设计方法研究.pdf

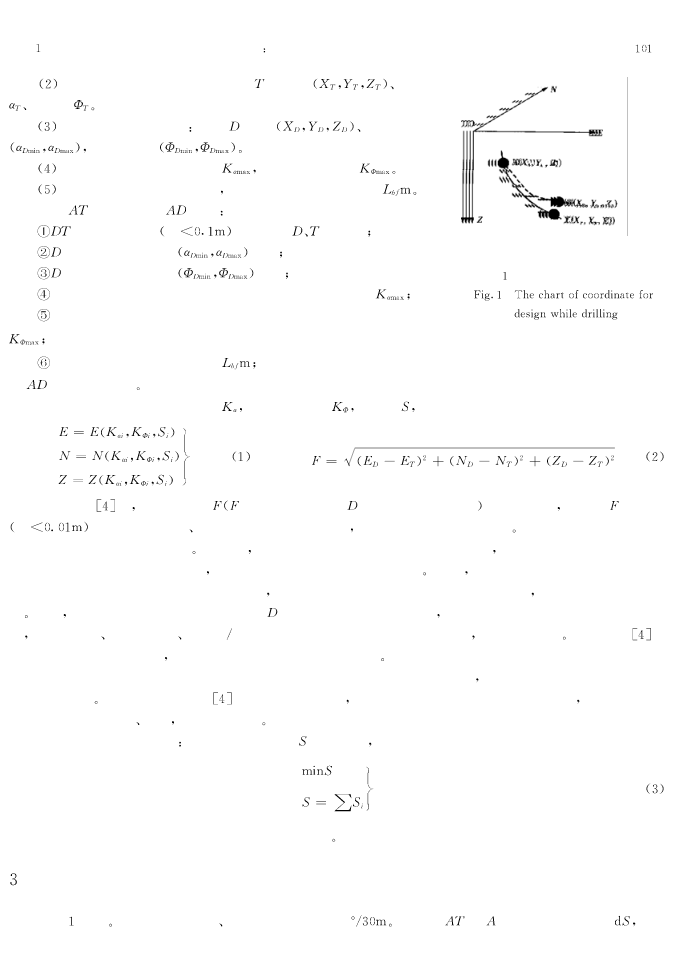
第))卷第#期石油学报NOPQ))MOQ#
)((#年#月6F46G54HIJ5KLKMKF6STUVTWXQ)((#
RRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR

文章编号!()*+,)-$%.)((#/(#,(#((,(*
水平井待钻井眼轨迹最优化设计方法研究

张焱#刘坤芳#曹里民#余雷#施太和)

.#0辽河石油勘探局工程技术研究院辽宁盘锦#)1(#(2)0西南石油学院石油工程系四川南充-+%((#/

摘要!现有待钻井眼轨迹设计的方法很多"涉及到二维方法和三维方法"但它们有一个共同的缺点"即设计出来的
井眼轨迹不能确信为一条最优的待钻轨迹或可行的最优待钻轨迹&为此"开展了本文的研究工作&本文将非线性不
等式约束下的非线性数学规划理论引入到水平井待钻井眼轨迹设计中"提出了水平井待钻井眼轨迹的最优化设计
方法&此方法不仅能够满足现场施工条件的限制和待钻井眼轨迹设计的要求"而且能够确保得到的待钻井眼轨迹
为一条最光滑的3最短的3可行的最优待钻井眼轨迹&文章最后的实例计算表明"本文提出的水平井待钻井眼轨迹
最优化设计方法是正确的3可靠的&

关键词!水平井2井眼轨迹2钻井设计2最优化2非线性规划
中图分类号!45))文献标识码!6

#引言

在定向井3水平井钻井中"由于诸多因素的影响实钻井眼轨迹往往偏离设计井眼轨迹&为了保证准确地钻
达靶区"当实钻井眼离开原设计井眼有较大偏差时"如不及时调整施工方案和措施"就有脱靶的危险&随钻修正
设计的目的就是为这种调整轨道施工提供理论依据"沿着这条新设计的理论轨道钻进"才能钻达预计的靶区&
因此"在钻井过程中进行轨道的修正设计是很有必要的&这种设计一般是三维的&目前关于待钻井眼轨迹设计
的方法很多"发表的文章和专著也不少"涉及到二维的设计方法和三维方法"如斜平面法7#83三维几何分析
法7)83简化方法7+83无约束最优化方法718等等&不同的方法有各自的优缺点"但它们有一个共同的缺点"就是设
计出来的井眼轨迹不能确信为一条最优的轨迹或可行的最优待钻轨迹&所谓最优轨迹就是在满足现场工具能
力的要求下"设计出来的轨迹具有最小的井斜角变化率3方位角变化率3最短的井深长度3最小的扭矩和摩阻力
等特点的井眼轨迹&这样的轨迹将大大减少可能的井下事故"缩短钻井周期"降低钻井成本"并将有利于后续作
业如完井3测试3修井和采注等作业的顺利进行&
为此"本文提出了水平井待钻井眼轨迹的最优化设计方法&本文将非线性不等式约束下的非线性规划方法
引入到水平井待钻井眼轨迹设计中"完善了文献718中的最优化设计理论"使之能够应用于水平井和侧钻水平
井3多底井9分支井的待钻设计&应用本文的方法可以优化出多种常见的轨迹形状"如变斜变方位:稳斜稳方
位2变斜变方位:稳斜稳方位:变斜变方位2变斜稳方位:稳斜变方位:稳斜稳方位2变斜变方位2稳斜变方位
:变斜稳方位:稳斜稳方位等等&

)设计思路

在进行待钻设计时"当前井底位置和井眼方向是确定的"同时"待钻设计目标点的位置和井眼方向也是明
确的&见图#"取东坐标;"北坐标<"垂深=建立三维坐标系><;=&假设现钻至?点"@为靶点"?@为设计
轨迹"?A为待钻轨迹"A为待钻轨迹上的一点&于是"待钻设计的基本已知条件为
当前井底坐标井斜角和方位角
.#/?.B?"C?"=?/3D?E?2
万方数据
作者简介!张焱"男"#$%#年#月生&#$$’年于西南交通大学获博士学位&现为辽河油田博士后科研流动站博士后&
第!期张焱等A水平井待钻井眼轨迹最优化设计方法研究!N!

作为目标的原设计轨道上某点的坐标井斜角
45674879:79;76<
方位角
=7<>7?
对设计终点的要求终点坐标井斜角范围
4@6AB48B9:B9;B6<
方位角范围
4=BC#09=BC*D694>BC#09>BC*D6?
现场工具的最大变斜能力最大变方位能力
4E6F=C*D9F>C*D?
根据动力钻具的使用情况变方位段长最好不能超过如
4G69HIJC?
设计轨迹K7与待钻轨迹KB满足A
LB7间距离足够小4如MNO!C6即可视为B<7点重合P
点的井斜角在范围以内
QB4=BC#09=BC*D6P
点的方位角在范围以内
RB4>BC#09>BC*D6P图!待钻设计坐标系示意图
待钻轨迹的最大变斜率小于现场工具的最大变斜能力
SF=C*DP"#$%!&’()’*+,-.)--+/#0*,(.-+
T待钻轨迹的最大变方位率小于现场工具的最大变方位能力/(1#$02’#3(/+#33#0$

F>C*DP
待钻轨迹中变方位段长小于
UHIJCP
则KB即为所求轨迹?
假设待钻轨迹的井斜变化率为方位变化率为段长