
结晶矿物岩石矿床学课件.ppt

qw****27






亲,该文档总共31页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

结晶矿物岩石矿床学课件.ppt
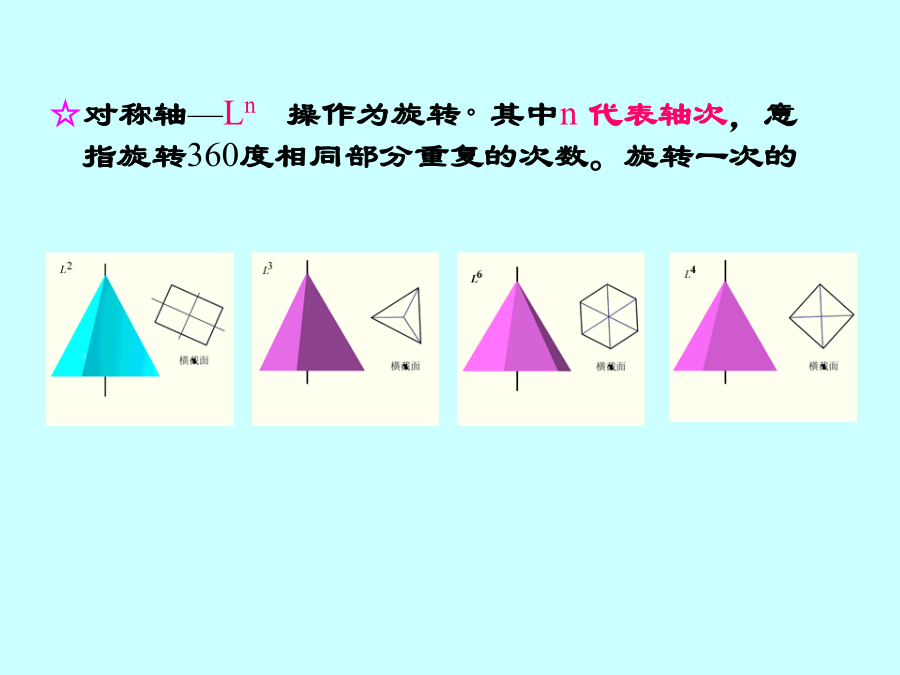
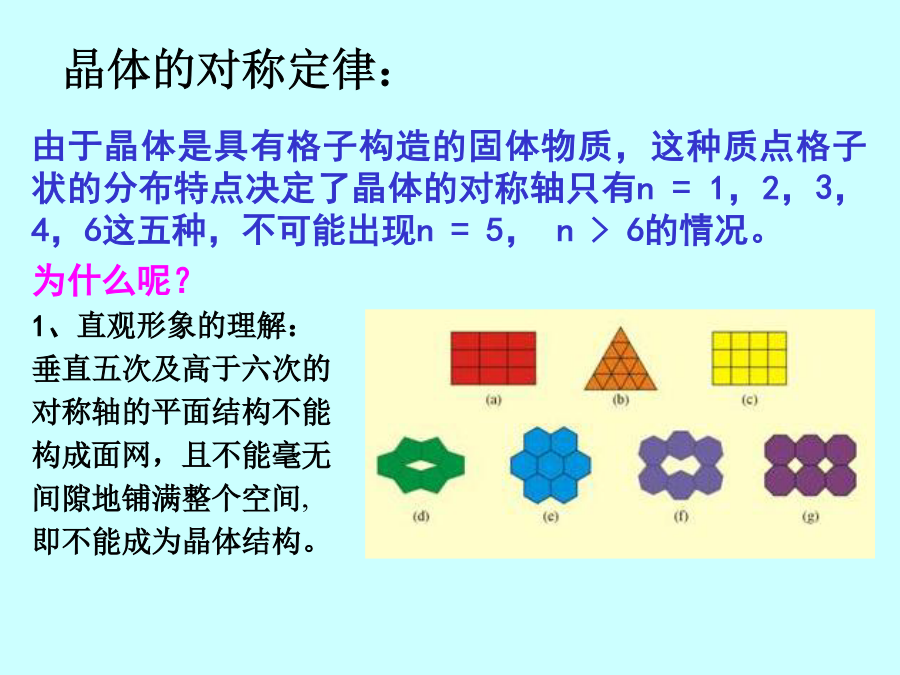
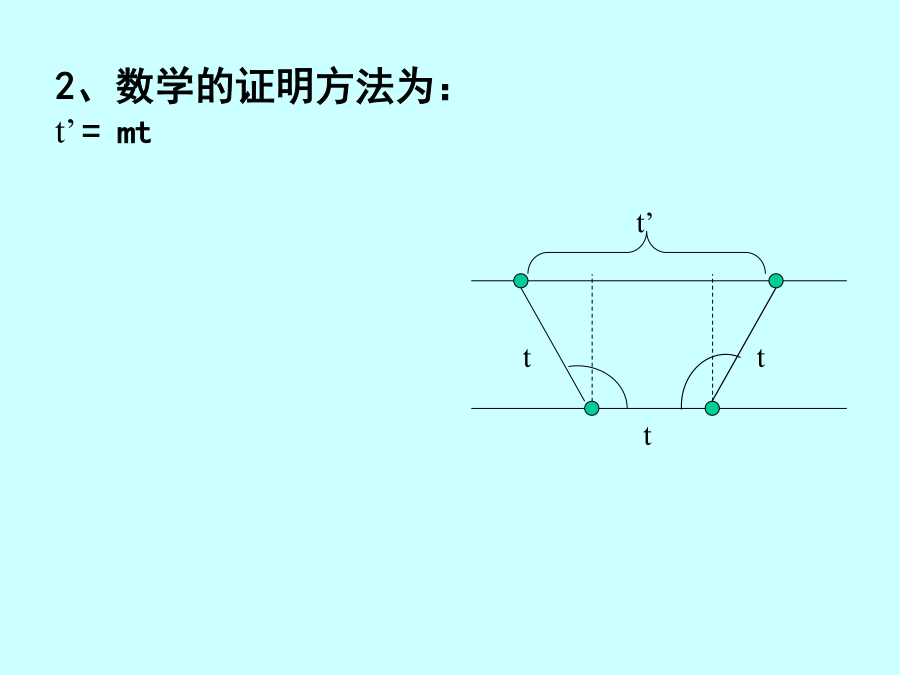
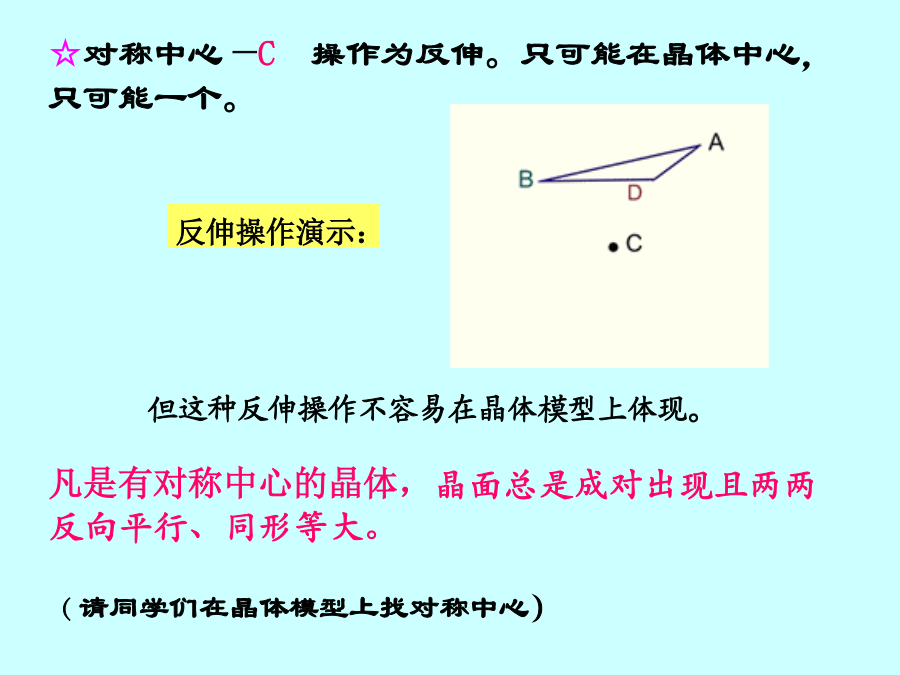
本章是晶体对称理论的主题部分,也是我们课程的重点。一、对称的概念对称就是物体相同部分有规律的重复。二、晶体对称的特点三、晶体的宏观对称要素和对称操作晶体外形可能存在的对称要素和相应的对称操作如下:☆对称面—P操作为反映。可以有多个对称面存在,如3P、6P等.(请同学们在晶体模型上找对称面:示范模型)☆对称轴—Ln操作为旋转。其中n代表轴次,意指旋转360度相同部分重复的次数。旋转一次的角度为基转角,关系为:n=360/。(请同学们在晶体模型上找对称轴)晶体的对称定律:2、数学的证明方法为:t’=mtt
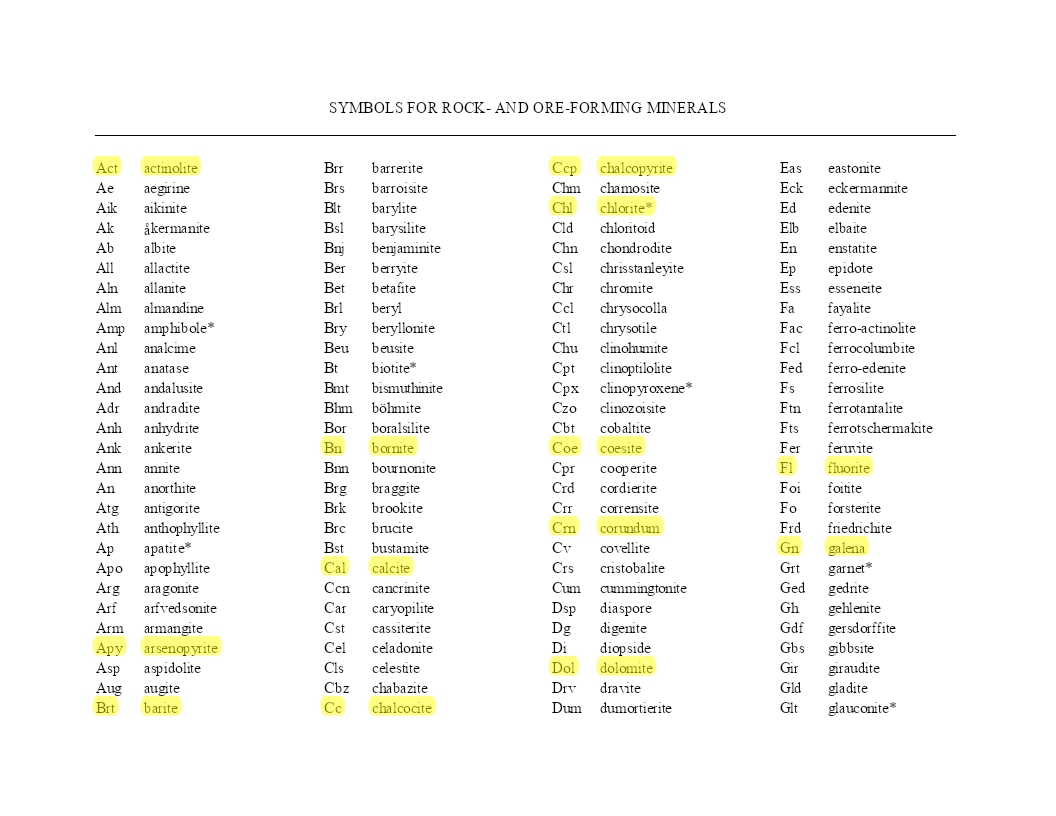
矿物缩写-岩石学、矿物学、矿床学.pdf
SYMBOLSFORROCK-ANDORE-FORMINGMINERALS____________________________________________________________________________________________________________ActactinoliteBrrbarreriteCcpchalcopyriteEaseastoniteAeaegirineBrsbarroisiteChmchamositeEckeckermanniteAikaikin

大学070901矿物学、岩石学、矿床学《712沉积岩石学》考.pdf

2012年 中国地质大学(北京) 矿物学、岩石学、矿床学及.doc

国内外矿物岩石矿床学教材对比研究报告.doc
国内外矿物、岩石、矿床学教材对比研究报告邱检生赵明陆建军岩石是构成固体地球(特别是岩石圈)的基本物质组成,绝大多数岩石均是由一种或数种造岩矿物按一定方式结合而成,矿床可以认为是岩石中某种有用元素达到可被工业利用、或岩石本身的工艺物理性能可被工业所利用的地质体。因此,矿物学、岩石学、矿床学课程是高校地质学和地球化学相关专业的一门十分重要的专业基础课。开展国内外该课相关教材的对比研究无疑有助于进一步提高教学效果,同时也将促进“双语化”教学课程的建设,为此,依托设置在南京大学的教育
