晶体对X射线的衍射.ppt

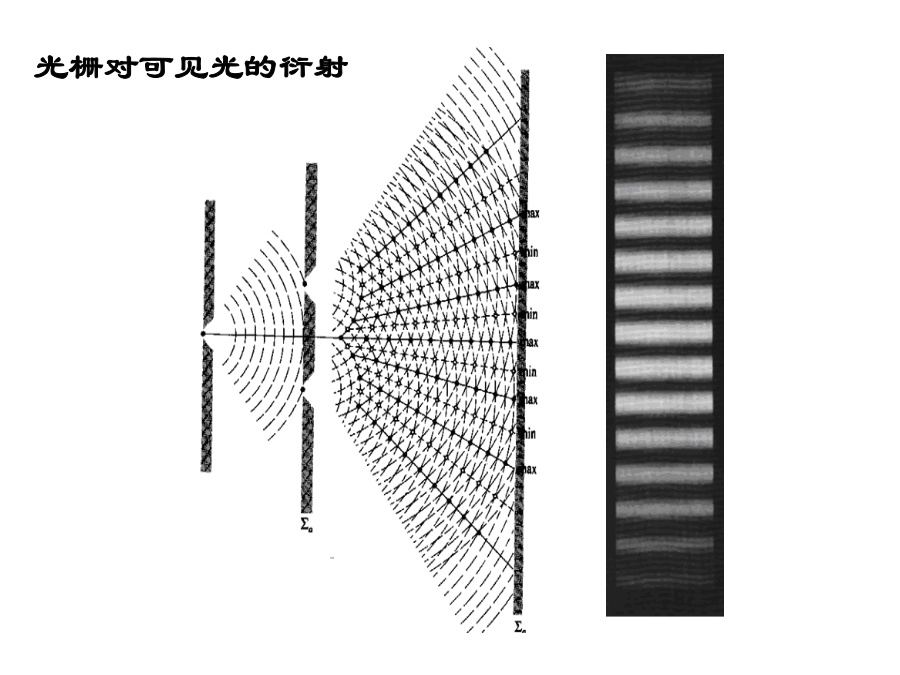
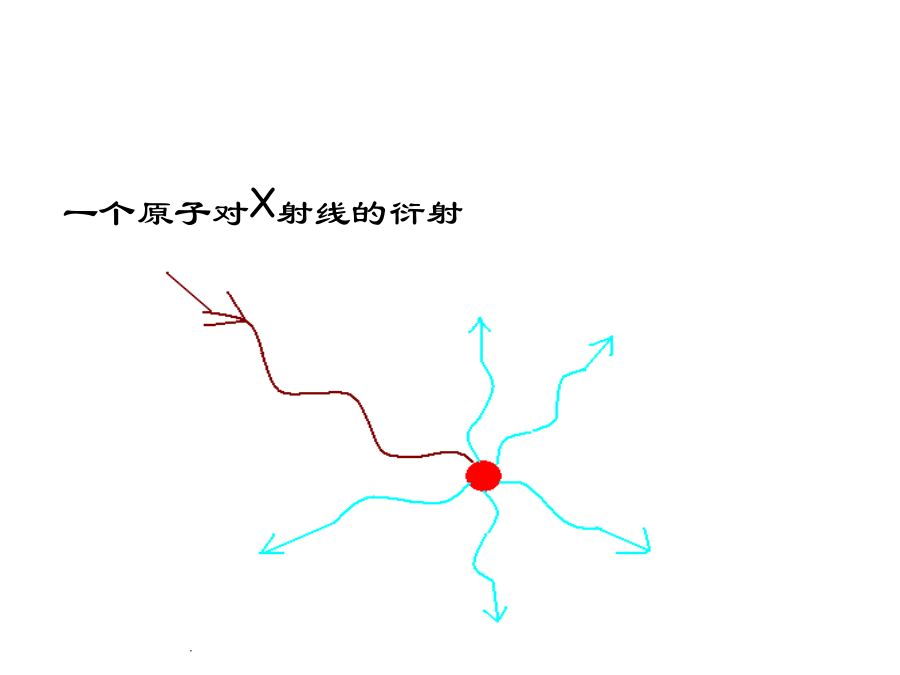
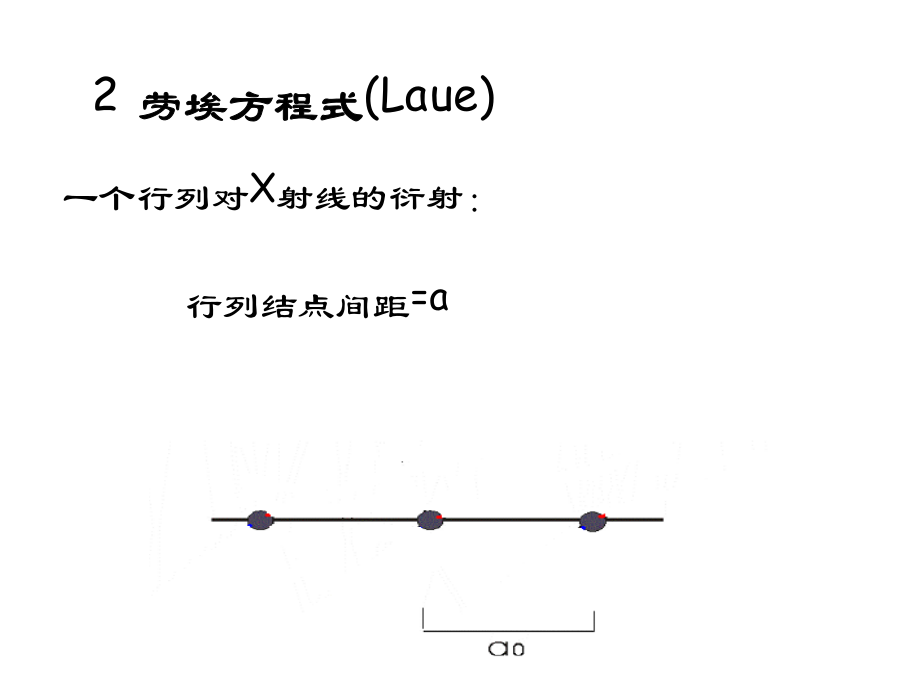
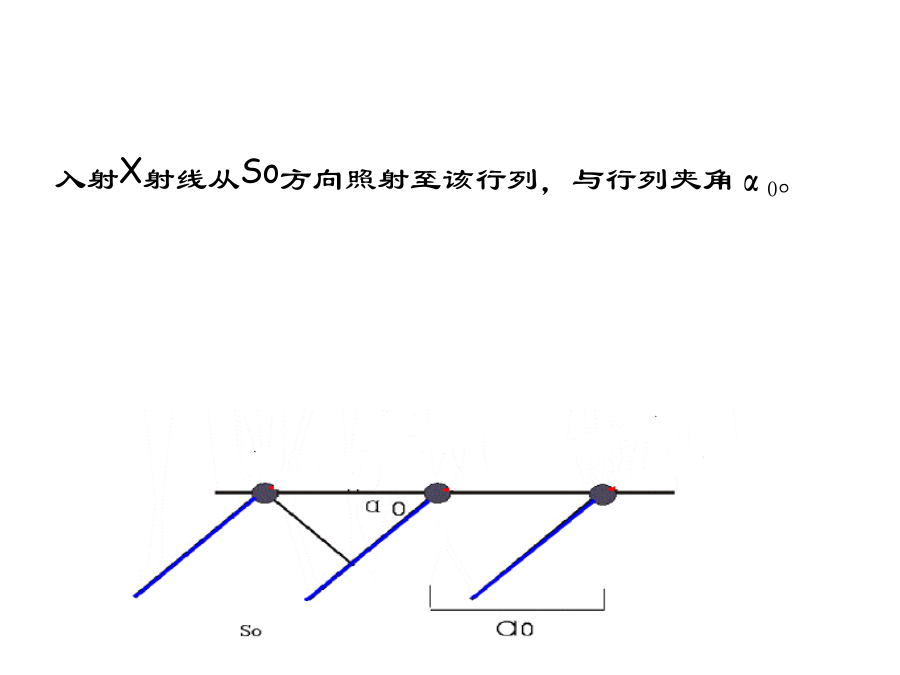
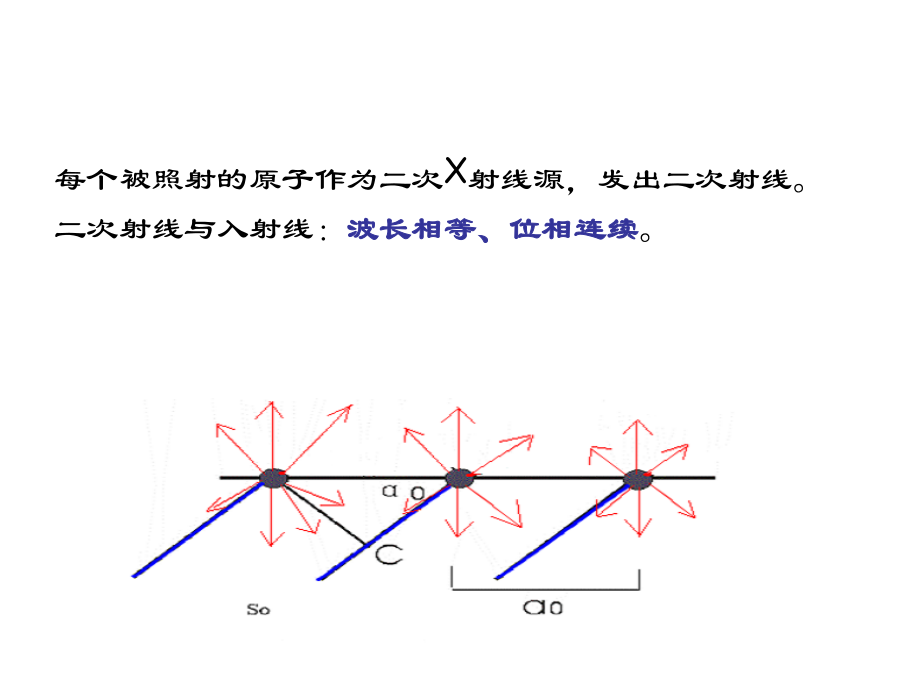
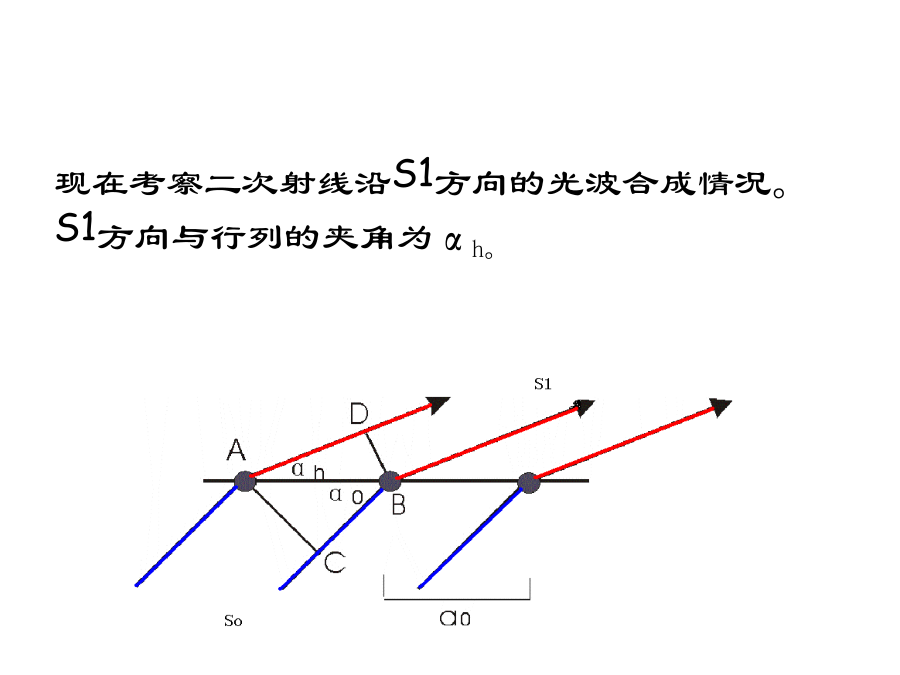
6晶体对X射线的衍射光栅对可见光的衍射1衍射的概念衍射方向决定于：
晶胞类型及单位晶胞几何形状。
衍射强度决定于：
晶胞中的原子种类、数量及其具体分布排列。

光波的合成条件：
1.波长相等；
2.光程差＝波长的整数倍一个原子对X射线的衍射实际上，原子对X射线的散射是通过核外电子进行的，如下式所示。2劳埃方程式(Laue)入射X射线从So方向照射至该行列，与行列夹角α0。每个被照射的原子作为二次X射线源，发出二次射线。
二次射线与入射线：波长相等、位相连续。
现在考察二次射线沿S1方向的光波合成情况。
S1方向与行列的夹角为αh。沿S1方向相邻原子产生的X射线的光程差为：
=AD–CB=ABcosαh－ABcosα0
=a0（cosαh－cosα0）
=hh=0,1,2……a0（cosαh－cosα0）=h
如果上式满足，即光程差等于波长的整数倍，即可产生衍射，衍射线与行列成αh角，即与行列夹角为αh的方向都可产生衍射，因此衍射线分布在一个圆锥面上，圆锥的半顶角为αh。h每等于一个整数值(0,1,2……)，即形成一个圆锥状衍射面，因此最终的衍射效果为一套圆锥。如下图所示：当入射方向为特殊方向(α0=90)时：
a0cosαh=h
cosαh=h/a0一个面网对X射线的衍射：
可以可作两个方向相交的行列：X行列和Y行列，其结点间距分别为ao，bo。入射线分别与其夹角为αo，βo。因此可按两个相交行列来考虑去衍射效应，满足两个行列的衍射方向，必须满足：

a0（cosαh－cosα0）=h
b0（cosβk－cosβ0）=k

h,k=0,1,2……

最终的衍射方向为两个方向圆锥（两套圆锥）的交线。同样道理，三个方向的结晶格子所形成的衍射为三个方向圆锥的公共交线：要满足的方程式为：
a0（cosαh－cosα0）=h
b0（cosβk－cosβ0）=k
c0（cosl－cos0）=l
h,k,l=0,1,2……
在直角坐标系的情况下，还有一个几何表达式：
cos2αh+cos2βk+cos2l=1

以上四个方程式统称为劳埃方程式。式中：
a0,b0,c0：晶胞轴长；α0,β0,0：入射线夹角；
αh,βk,l：衍射线夹角；为X射线的波长。
h,k,l：整数,（衍射指数,等同于面网符号)3布拉格方程式(Bragg)沿So方向，入射光与面网以夹角θ照射到面网上。假定沿S1方向，产生了光的“反射”，入射角=反射角。但在一般情况下，X射线不具有反射性质。(只有在入射角非常小的情况下，约小于20’才可能产生全反射)。
如果相邻面发射的X射线光程差等于波长的整数倍时，由于光的干涉作用，反射可以成立。
现在来考察相邻面之间反射的X射线的光程差。=BM+BN=2dhklsinθ
如果=nλ，即光程差等于波长的整数倍，这时面网对X射线的反射可以成立。
即反射成立的条件为
nλ=2dhklsinθnλ=2dsinθ

式中n为1，2，3，……等整数，称为衍射级数。θ为入射角，或半衍射角。
该式即称为布拉格方程，是X射线晶体学中最基本的方程之一。根据布拉格方程，我们可以把晶体对X射线的衍射看作为“反射”。
但是，这种“反射”并不是任意入射角都能产生的，只有符合布拉格方程的条件才能发生，故又常称为“选择反射”。
据此，每当我们观测到一束衍射线，就能立即想象出产生这个衍射的面网的取向，并且由半衍射角θ便可依据布拉格方程计算出这组面网的面网间距（当波长已知时）。对劳埃方程式变形后：
（cosαh－cosα0）=h/a
（cosβk－cosβ0）=k/b
（cosl－cos0）=l/c
左边的平方和经数学变换后为4sin2
右边的平方和为(h2/a2+k2/b2+l2/c2)2=2/dhkl2

因此有＝2dhklsin此为布拉格方程式的标准形式比较二者：普通形式：n＝2dsin
标准形式：＝2dhklsin
n为衍射级次，当n＝1时，二者完全一致。当n>1时，＝2d/nsin，dhkl＝d/n
如n＝2，例如：d001/2=d002
即2＝2d001sin001面网的二级衍射可以看作＝2d002sin002面网的一级衍射，而后者可以是晶体中实际存在的面网，也可以是假想的。
在使用时，一般只考虑其标准形式。001面网的2级衍射被看作002面网的1级衍射图示：2θ(2)根据＝2dsin可知：
面网间距d越大，衍射角度2越小。反之，随着衍射角度2θ的增加，对应的d值越小。(3)根据＝2dsin，获得d值，根据d＝/(2sin)，从而产生了两种不同类型的X射线衍射方法：

a）改变波长：劳埃照相方法，在X射线分析中，该方法已淘汰，但却广泛应用于同步辐射中，其