
《多元线性回归》.ppt

17****92









亲,该文档总共102页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《多元线性回归》.ppt
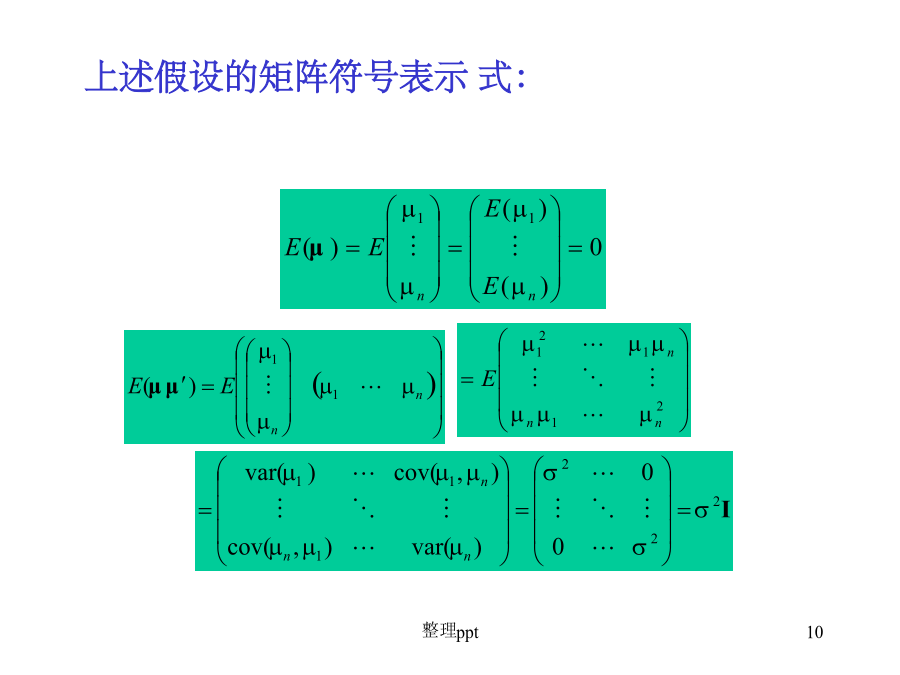
经典单方程计量经济学模型:多元线性回归模型§3.1多元线性回归模型一、多元线性回归模型也被称为总体回归函数的随机表达形式。它的非随机表达式为:总体回归模型n个随机方程的矩阵表达式为:6其随机表示式:二、多元线性回归模型的基本假定假设3,解释变量与随机项不相关上述假设的矩阵符号表示式:f(u)假设4,向量有一多维正态分布,即其中:Q为一非奇异固定矩阵,矩阵x是由各解释变量的离差为元素组成的nk阶矩阵§3.2多元线性回归模型的估计一、普通最小二乘估计于是得到关于待估参数估计值的正规方程组:□正规方程组的矩
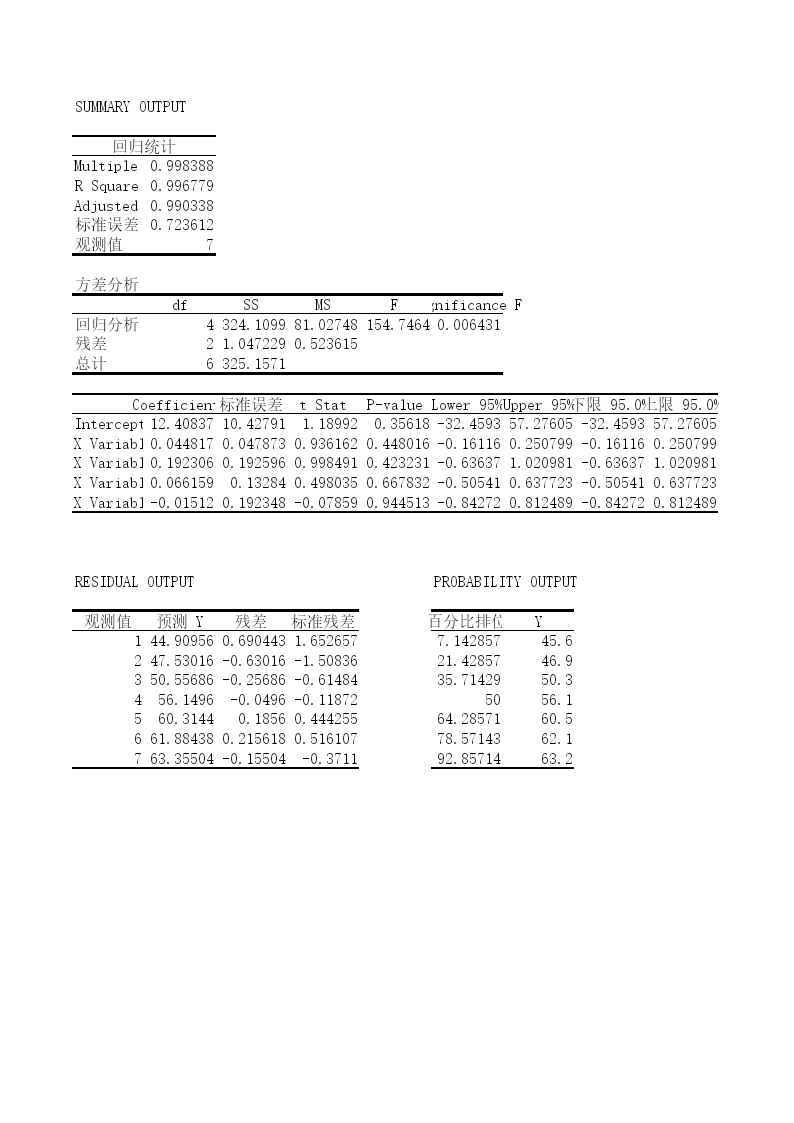
多元线性回归.xls
SUMMARYOUTPUT回归统计MultipleR0.997484853RSquare0.994976031AdjustedRSquare0.984928093标准误差0.916147249观测值7方差分析dfSSMSFSignificanceF回归分析4332.449919983.1124799799.022908330.010022698残差21.6786515640.839325782总计6334.1285714Coefficients标准误差tStatP-valueLower95%Upper95

多元线性回归().pdf

多元线性回归.pdf

多元线性回归.ppt
多元线性回归多元线性回归内容安排多元线性回归模型与参数估计参数的最小二乘估计回归方程和偏回归系数的假设检验偏回归系数的假设检验回归方程的假设检验若拒绝H0,则可分别对每一个偏回归系数bj作统计检验,实质是考察在固定其它变量后,该变量对应变量Y的影响有无显著性。H0:Bj=0H1:Bj不为零=0.05F=(Xj的偏回归平方和/1)/MS误差Xj的偏回归平方和:去Xj后回归平方和的减少量若H0成立,可把Xj从回归方程中剔除,余下变量重新构建新的方程。标准化偏回归系数和确定系数确定系数:简记为R2,即回归平方
