
《X线成像理论》.ppt

15****92









亲,该文档总共109页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

X线成像理论.ppt
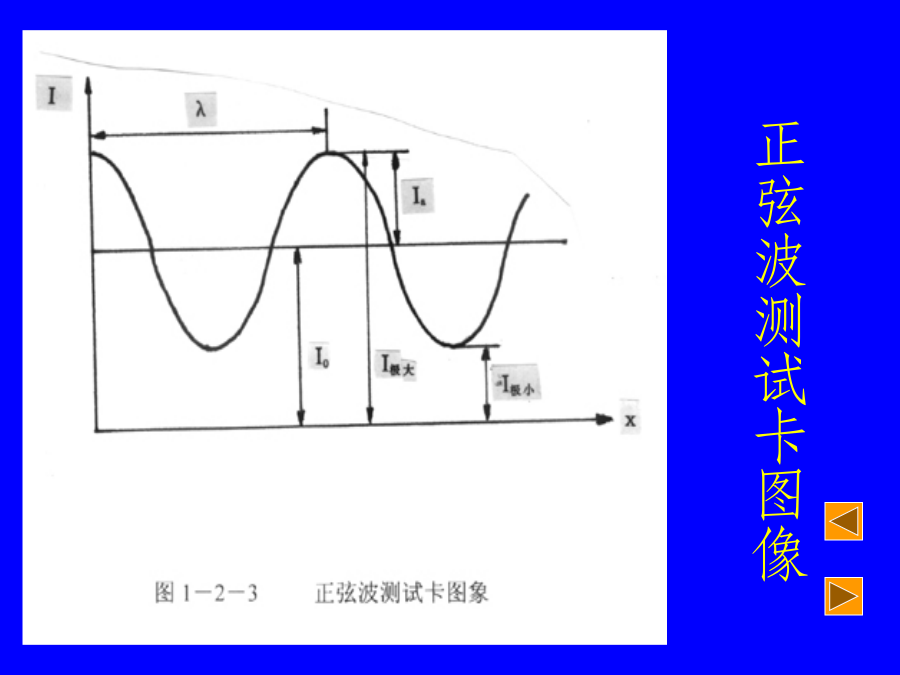
光学传递函数简介空间频率和调制度2.描述时间性周期性变化的参量对于波动性的周期性变化来说二、空间频率矩形波测试卡正弦波测试卡2.描述空间性周期性变化的参量正弦波测试卡图像三、最简单的空间性周期性变化四、对比度与调制度调制度光学传递函数的定义一、光学成像的一般特点正弦波测试卡的光强分布4.物经成像系统成像之后,其初相位要发生变化5.调制度的物理意义调制度是物中细节光强与相对背景光强之差,人们根据调制度的大小来看到和分辨物体。例如:白天放电影比不上晚上的清楚,因此,光学成像系统成像的实质是对调制度的传递。二、

《X线成像理论》.ppt
光学传递函数简介空间频率和调制度2.描述时间性周期性变化的参量对于波动性的周期性变化来说二、空间频率矩形波测试卡正弦波测试卡2.描述空间性周期性变化的参量正弦波测试卡图像三、最简单的空间性周期性变化四、对比度与调制度调制度光学传递函数的定义一、光学成像的一般特点正弦波测试卡的光强分布4.物经成像系统成像之后,其初相位要发生变化5.调制度的物理意义调制度是物中细节光强与相对背景光强之差,人们根据调制度的大小来看到和分辨物体。例如:白天放电影比不上晚上的清楚,因此,光学成像系统成像的实质是对调制度的传递。二、

X线成像基础理论.ppt
第二章X线成像基础理论第二章X线成像基础理论教学内容教学重点、难点第一节X线管焦点及X线量分布二、X线量分布特点X线束第二节X线照片影像X线影像信息传递1、X线照射不均匀密度和不等原子的肢体后,带有强度不均匀的X线信息。2、将不均匀的X线强度分布,通过(增感屏-胶片系统、荧光屏、影像增强系统、电影等)转成二维图像。3、观片等4、通过视网膜观察图像5、传给人脑综合分析二、X线影像的观察方法(一)X线透视法:优点观察器官的运动情况,可以多方位观察病灶,观察骨折复位情况,用于胸透等。缺点:不能留下记录,观察细微

X线成像基础理论.ppt
X线成像基础理论三第五节散射线及其消除一、散射线一、散射线一、散射线一、散射线5一、散射线50一、散射线二、散射线对照片对比度的影响二、散射线对照片对比度的影响显然,散射线导致照片上的光学对比度的损失为:三、散射线的抑制与消除三、散射线的抑制与消除三、散射线的抑制与消除遮线筒缩线器(电动和手调)三、散射线的抑制与消除滤过板(铝板、铜复合板)三、散射线的抑制与消除三、散射线的抑制与消除三、散射线的抑制与消除静止式(2)滤线栅的分类(2)滤线栅的分类(2)滤线栅的分类(2)滤线栅的分类对比两张腹部平片(摄影片

X线成像理论中级专业知识X线摄影条件.pdf
X线成像理论中级专业知识X线摄影条件一、感光效应与摄影条件选择(一)概念X线感光效应指X线通过被检体后使感光系统(屏片系统)感光的效果。摄影条件的制定是以指数函数法则作为基础理论,其具体内容是:若远离焦点的X线为平行的,则X线通过肢体后给予胶片的X线能可近似用下式表示:其中:V代表管电压,i代表管电流,t代表摄影时间,s代表增感率,f代表胶片的感度,z代表焦点物质的原子序数,r代表摄影距离,B代表曝光量倍数,D代表照射野的面积(cm2),e是自然对数的底,μ代表减弱系数,d代表被检物体的厚度(cm)。以使
