内容提供者
《运筹学》胡运权清华版-8-04最大流.ppt
2024-08-05
20金币
192KB
20页
15****92
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共20页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
《运筹学》胡运权清华版-8-04最大流.ppt
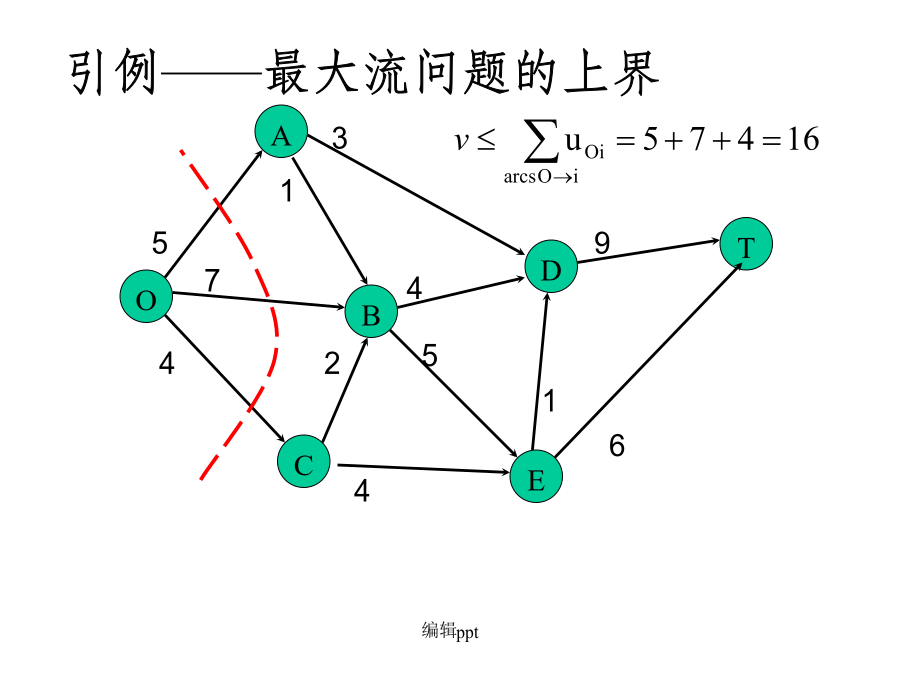
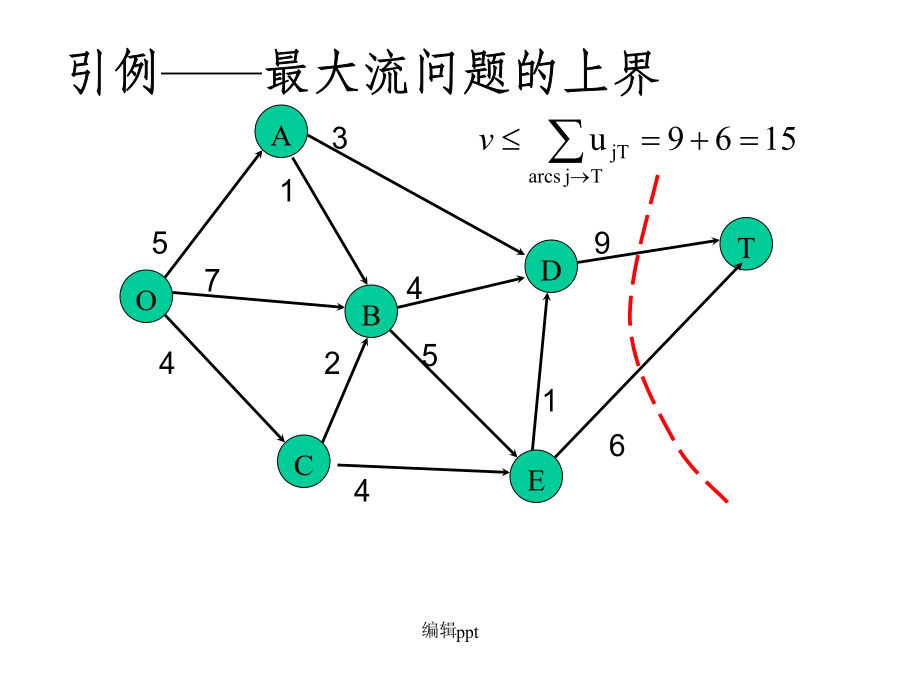
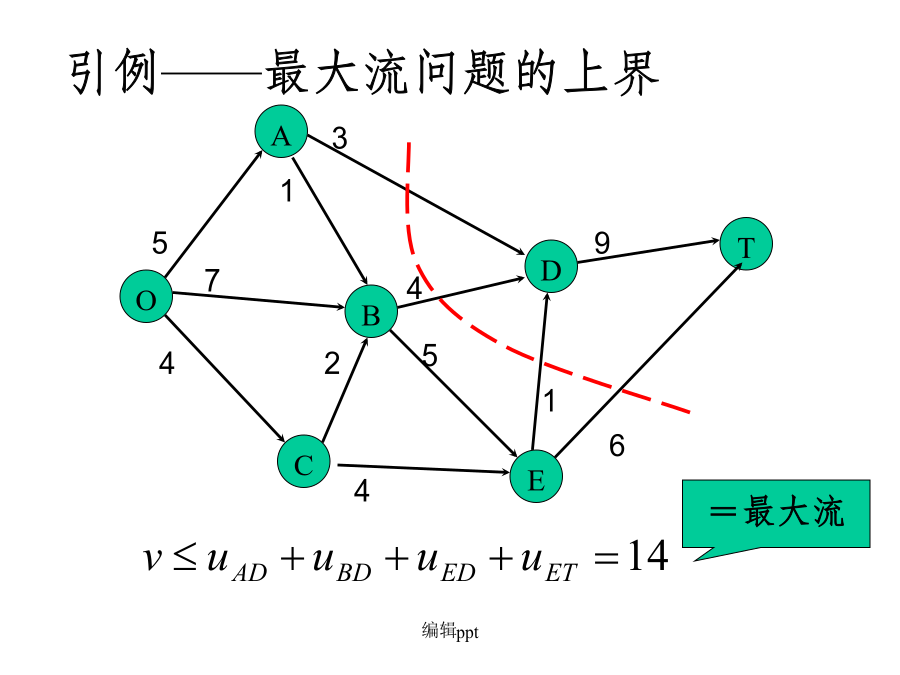
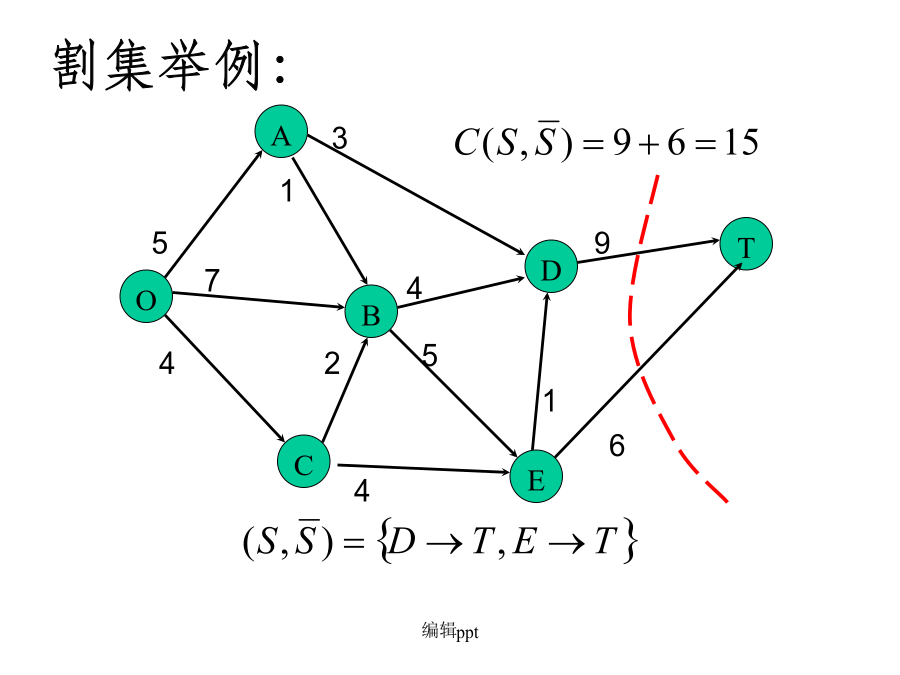
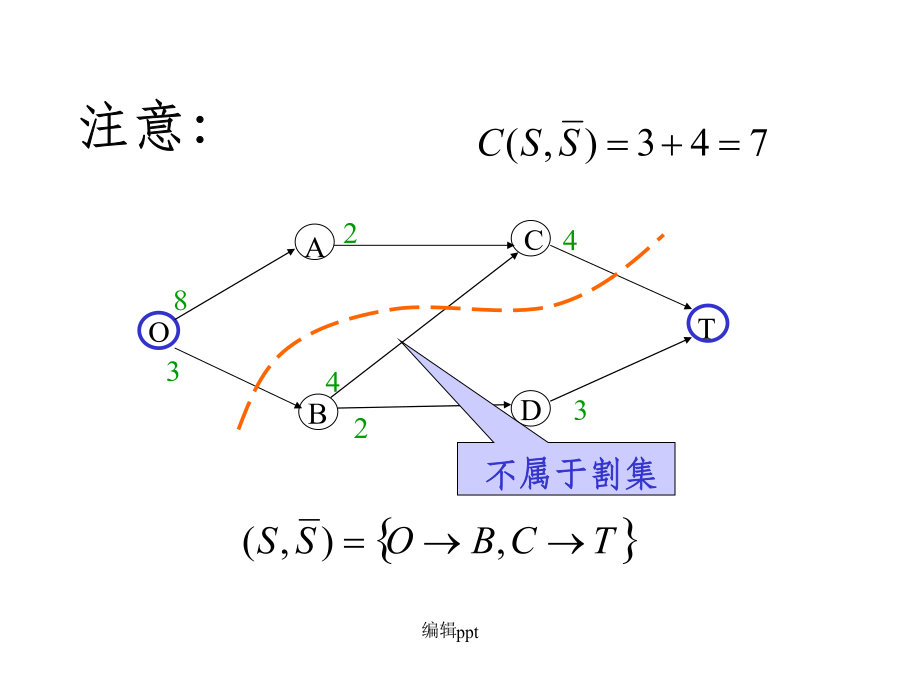
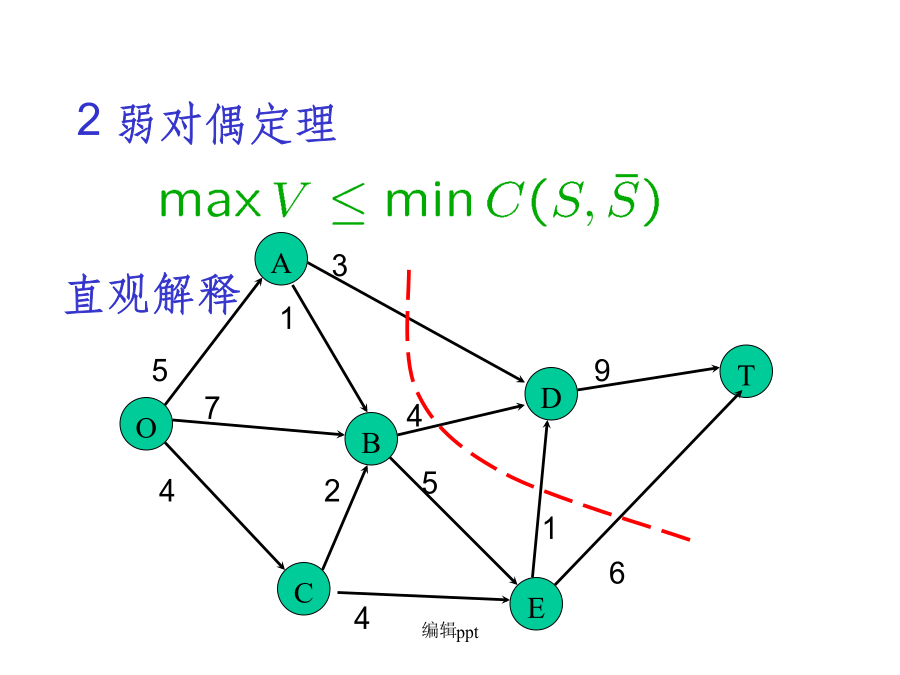
五.最大流最小割定理（Max-flowmin-cutTheorem）AAA若割集举例：割集举例：割集举例：82弱对偶定理2.弱对偶定理显然，若对某个可行流x*，在网络中有一个割集,满足则x*必定是最大流，是最小割。3强对偶定理——最大流最小割定理最小割举例（1）寻找增广链；（2）若找不到增广链时（即已找到最大流），记步骤（1）中已连节点集合为S；（3）即为所求。最小割的求法举例A5最小割的实际意义六、最大匹配问题是否存在从s到t的最大流?
2024-08-05
20
192KB
《运筹学》胡运权清华版-绪论.ppt
2024-08-05
20
182KB
《运筹学》胡运权清华版-1-07 其他应用例子.ppt
第七节其他应用例子一、混合配料问题一、混合配料问题一、混合配料问题一、混合配料问题一、混合配料问题二、产品计划问题二、产品计划问题二、产品计划问题二、产品计划问题二、产品计划问题二、产品计划问题二、产品计划问题利润＝销售收入－加工费－原料费月份产品月份产品月份产品三、生产存贮问题三、生产存贮问题月份产品月份产品三、生产存贮问题三、生产存贮问题三、生产存贮问题三、生产存贮问题四、动态投资问题第七节其他应用例子
2024-08-05
20
529KB
《运筹学》胡运权清华版-3-04 运输问题应用.ppt
生产计划问题产量或销量有上下限的运输问题船舶调度问题生产计划问题季度25交货季生产季交货季生产季x=150001002015000010200000020Minz=913.5产量或销量有上下限的运输问题例7例7使用生产例7使用生产使用生产使用生产使用生产练习单价船舶调度问题例8某公司承担4条航线的运输任务。已知：（1）各航线的起点、终点及每天的航班数（2）各城市之间的航行时间（3）所有航线都使用同一种船只，每次装船和卸船时间均为一天。问：该公司至少要配备多少条船才能满足所有航线运输的需要？解：所需配备船只
2024-08-05
20
283KB
《运筹学》胡运权清华版-5-05指派问题.ppt
第五节指派问题例、有四项任务需分派给甲、乙、丙、丁四个人去做，这四个人都能承担上述四项任务，但完成各项任务所需时间如下表所示。问应如何分派任务可使完成任务的总工时最少？解：设决策变量xij,i＝1,2,3,4;j＝1,2,3,4约束条件：目标：min（总时间）推广——指派问题的数学模型二、指派问题的解的特点可行解：每行有且仅有一个1；每列有且仅有一个1；其余均为0。例三、指派问题的求解方法——匈牙利法源于Konig的两个定理证明分析：若C=(cij)n×n的第一行各元素分别加上一个常数k，得到一个新矩阵C
2024-08-05
20
326KB