参数估计的相关问题.pptx

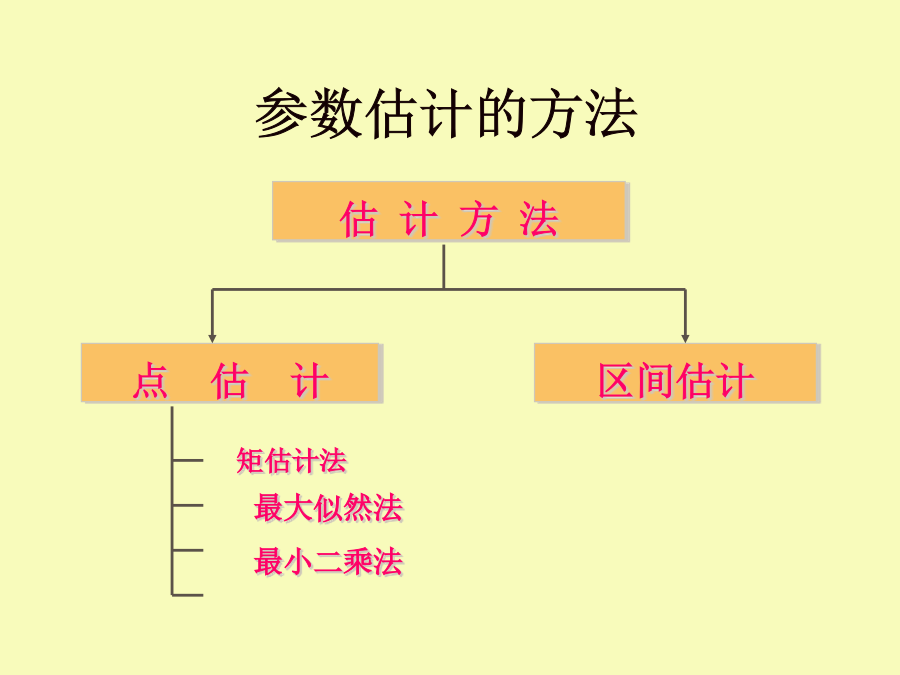
参数估计的相关问题第七章参数估计7.1参数估计的一般问题7.1.1.估计量与估计值统计估计的基本过程：1）.通过样本获取一些基本的统计量，然后利用这些基本统计量与总体参数之间的联系，（获得统计量的分布）利用有关统计方法，估计总体参数。2）.由此可以看出，统计量与总体参数、估计量的不同：总体参数通常是未知的定数，是待估计量；统计量是根据样本计算的函数，通常是随机变量（对于总体而言）；估计量用来对总体参数进行估计的统计量。参数估计的方法7.1.2.点估计与区间估计点估计(pointestimate)具体方法7.1.2评价估计量的标准（一般含义）1、无偏性：，称是的无偏估计量。2、有效性。一个具有较小变异的统计量的意义在于将有更多的机会产生一个更接近于总体参数的量。3、一致性。随着样本容量的增大，点估计量的值越来越接近被估计总体参数。无偏性(unbiasedness)有效性(efficiency)一致性(consistency)为的无偏、有效、一致估计量；为的无偏、有效、一致估计量为的无偏、有效、一致估计量。7.1.3区间估计(intervalestimate)区间估计的数学表达方式：区间估计的图示将构造置信区间的步骤重复很多次，置信区间包含总体参数真值的次数所占的比例称为置信水平表示为(1-为是总体参数未在区间内的比例常用的置信水平值有99%,95%,90%相应的为:0.01，0.05，0.10的值:2.58,1.96,1.645(记住)置信区间与置信水平影响区间宽度的因素p2071.置信水平为95%的置信区间，意思是在构造的所有置信区间当中，包含总体参数真值的区间占95%。2.总体参数的真值是固定的、未知的，而用样本构造的置信区间是不固定的。一个样本构造一个区间，不同样本构造不同的区间，因此置信区间是随机区间。置信水平是针对随机区间而言，不是所有区间都包含总体参数的真值。3.在实际问题中，进行估计时，往往只抽取一个样本。由该样本所构造的区间是一个特定的区间，而不再是随机区间，因此该区间是否包含总体参数的真值，我们是不知道的。7.2一个总体参数的区间估计p2111.一个总体参数的区间估计7.2.1总体均值的区间估计(大样本)总体均值的区间估计(例题分析)总体均值的区间估计(例题分析)总体均值的区间估计(例题分析)总体均值的区间估计(例题分析)计算样本统计量STAT正态总体或非正态总体但大样本，总体方差未知总体均值的区间估计(小样本)正态总体小样本，总体方差未知p214总体均值的区间估计(例题分析)P175总体均值的区间估计(例题分析)均值推断方法的选择p2177.2.2.总体比例的区间估计总体比例的区间估计(例题分析)P2187.2.3总体方差的区间估计总体方差的区间估计(图示)总体方差的区间估计(例题分析)总体方差的区间估计(例题分析)7.2.4正态总体未来观察值的预测区间估计p220未来观察值的预测区间估计p222区间估计练习7.3两个总体参数的区间估计两个总体参数的区间估计7.3.1两个总体均值之差的估计(大样本)两个总体均值之差的估计(大样本)两个总体均值差的估计(例题分析)两个总体均值差的估计(例题分析)两个总体均值差的估计(小样本:12=22)两个总体均值差的估计(小样本:12=22)两个总体均值差的估计(例题分析)两个总体均值差的估计(例题分析)两个总体均值差的估计(小样本:1222)两个总体均值差的估计(小样本:1222)两个总体均值之差的估计(例题分析)解:根据样本数据计算得自由度为：两个总体均值之差的估计(例题分析)1.假定条件两个总体服从二项分布可以用正态分布来近似两个样本是独立的2.两个总体比例之差1-2在1-置信水平下的置信区间为两个总体比例之差的估计(例题分析)两个总体比例之差的估计(例题分析)两个总体方差比的区间估计两个总体方差比的区间估计(图示)两个总体方差比的区间估计(例题分析)两个总体方差比的区间估计(例题分析)7.4样本容量的确定(P234)估计总体均值时样本容量n为样本容量n与总体方差2、边际误差E、可靠性系数Z或t之间的关系为与总体方差成正比与边际误差成反比与可靠性系数成正比估计总体均值时样本容量确定(例题分析)估计总体均值时样本容量确定(例题分析)1.根据比例区间估计公式可得样本容量n为估计总体比例时样本容量确定(例题分析)确定样本容量时注意：设n1和n2为来自两个总体的样本，并假定n1=n2根据均值之差的区间估计公式可得两个样本的容量n为估计两个总体均值之差时样本容量的确定(例题分析)估计两个总体均值之差时样本容量的确定(例题分析)设n1和n2为来自两个总体的样本，并假定n1=n2根据比例之差的区间估计公式可得两个样本的容量n为估计两个总体