
立体几何中的翻折问题资料.ppt

天天****心情





亲,该文档总共12页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

立体几何中的翻折问题资料.ppt
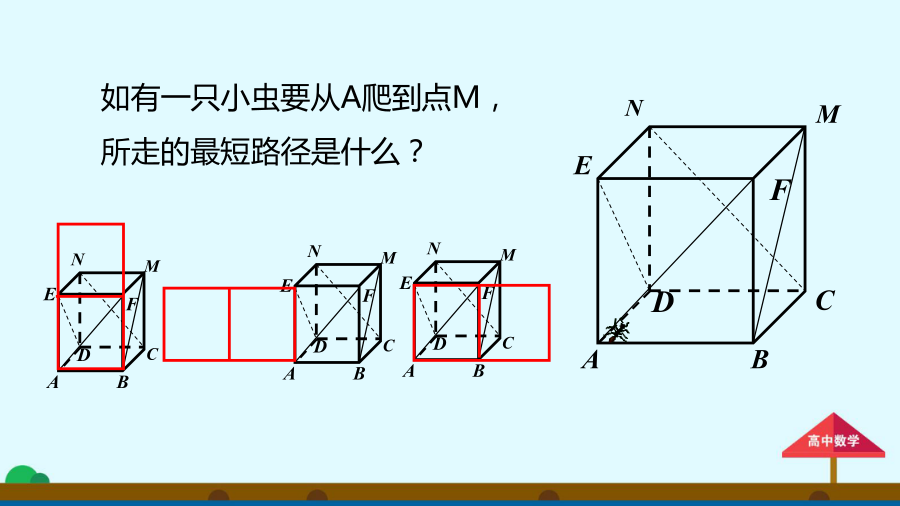
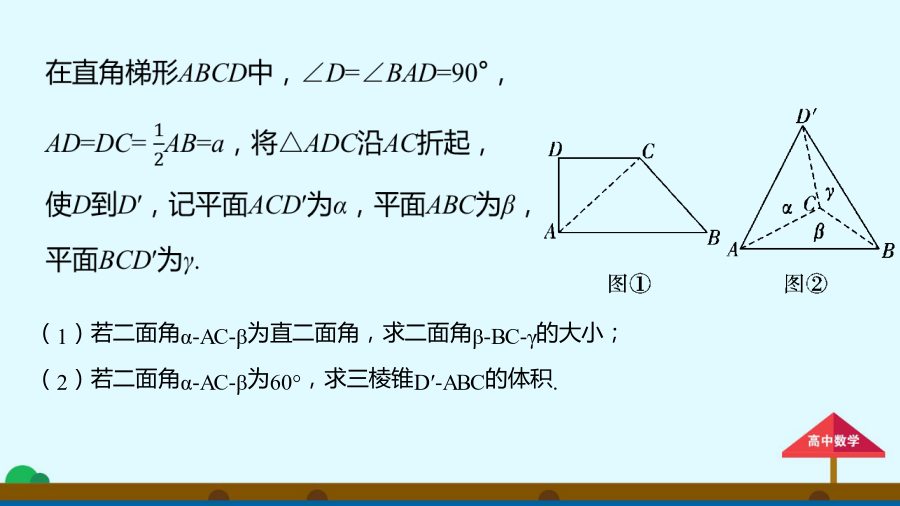
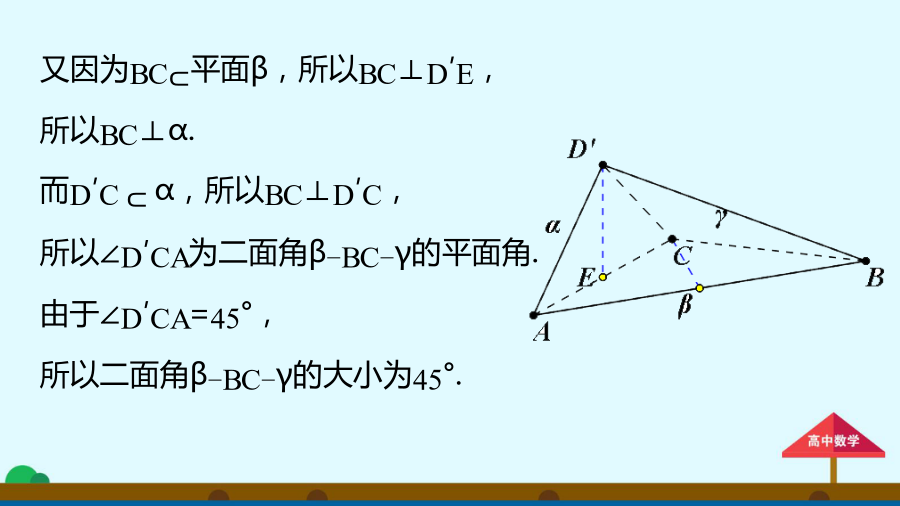
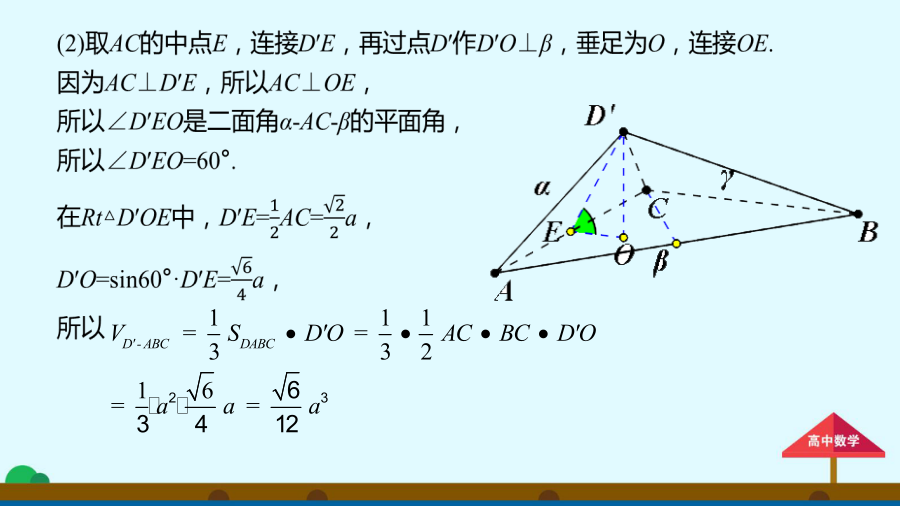
立体几何中的翻折问题图形的展开与翻折问题就是一个由抽象到直观,由直观到抽象的过程.在历年高考中以图形的展开与折叠作为命题对象时常出现,因此,关注图形的展开与折叠问题是非常必要的.(1)先比较翻折前后的图形,弄清哪些量和位置关系在翻折过程中不变,哪些已发生变化;(2)将不变的条件集中到立方体图形中,将问题归结为一个条件与结论明朗化的立几问题.又因为BC⊂平面β,所以BC⊥D′E,所以BC⊥α.而D′C⊂α,所以BC⊥D′C,所以∠D′CA为二面角β-BC-γ的平面角.由于∠D′CA=45°,所以二面角β-B

立体几何的翻折问题.doc
1.△ABC的BC边上的高线为AD,BD=a,CD=b,将△ABC沿AD折成大小为θ的二面角B-AD-C,若,则三棱锥A-BCD的侧面三角形ABC是()A、锐角三角形B、钝角三角形C、直角三角形D、形状与a、b的值有关的三角形如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:ABCDEFMN①点M到AB的距离为②三棱锥C-DNE的体积是③AB与EF所成角是其中正确命题的序号是4.将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线与是异面直线的是……………

立体几何的翻折问题.pptx

立体几何的翻折问题.ppt
立体几何的动态问题之———翻折问题点动问题;线动问题;面动问题;体动问题;多动问题等一、面动问题(翻折问题)(二)翻折问题的一线五结论二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题课堂小结课堂小结衷心感谢各位专家的指导!二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题AF

立体几何中的翻折问题作业.doc
立体几何中的翻折问题姓名1.(昆明一中月考理)图甲,直角梯形中,∥,,点分别在上,且,现将梯形沿拆起,平面平面,图乙.(Ⅰ)求证:∥平面ACBDNMCDNABM甲乙(Ⅱ)若二面角的大小为,求线段的长;2.(三明市三校联考)如图,ABCD是块矩形硬纸板,其中AB=2AD=2,E为DC中点,将它沿AE折成直二面角D-AE-B.ABCEDCDEAB(Ⅰ)求证:AD⊥平面BDE;(Ⅱ)求二面角B-AD-E的余弦值.3.(湖南•理•18题)如图1,分别是矩形的边的中点,是上的一点,将,分别沿翻折成,,并连结,使得平
