python线性回归实验——【机器学习与算法分析】.pdf

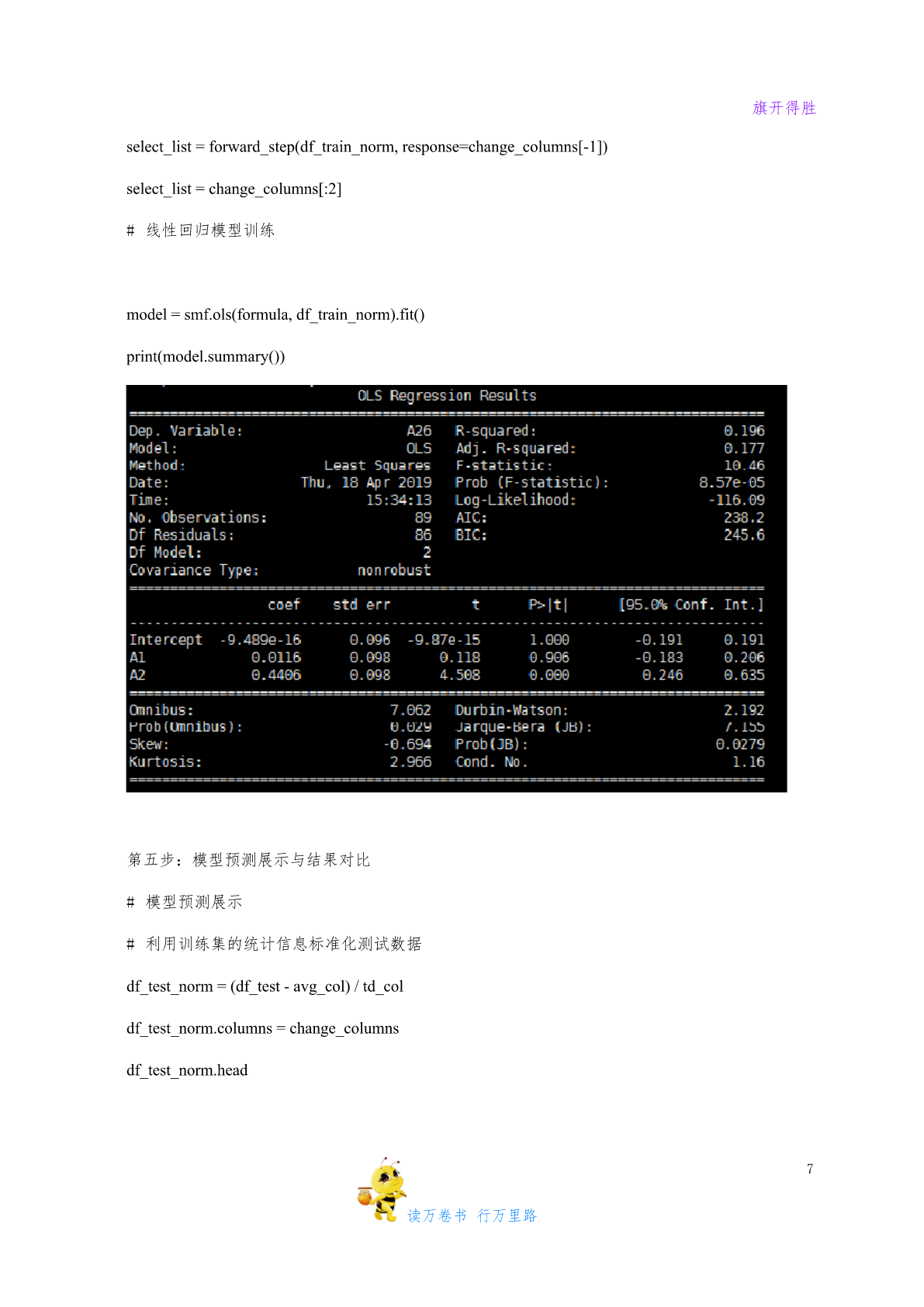
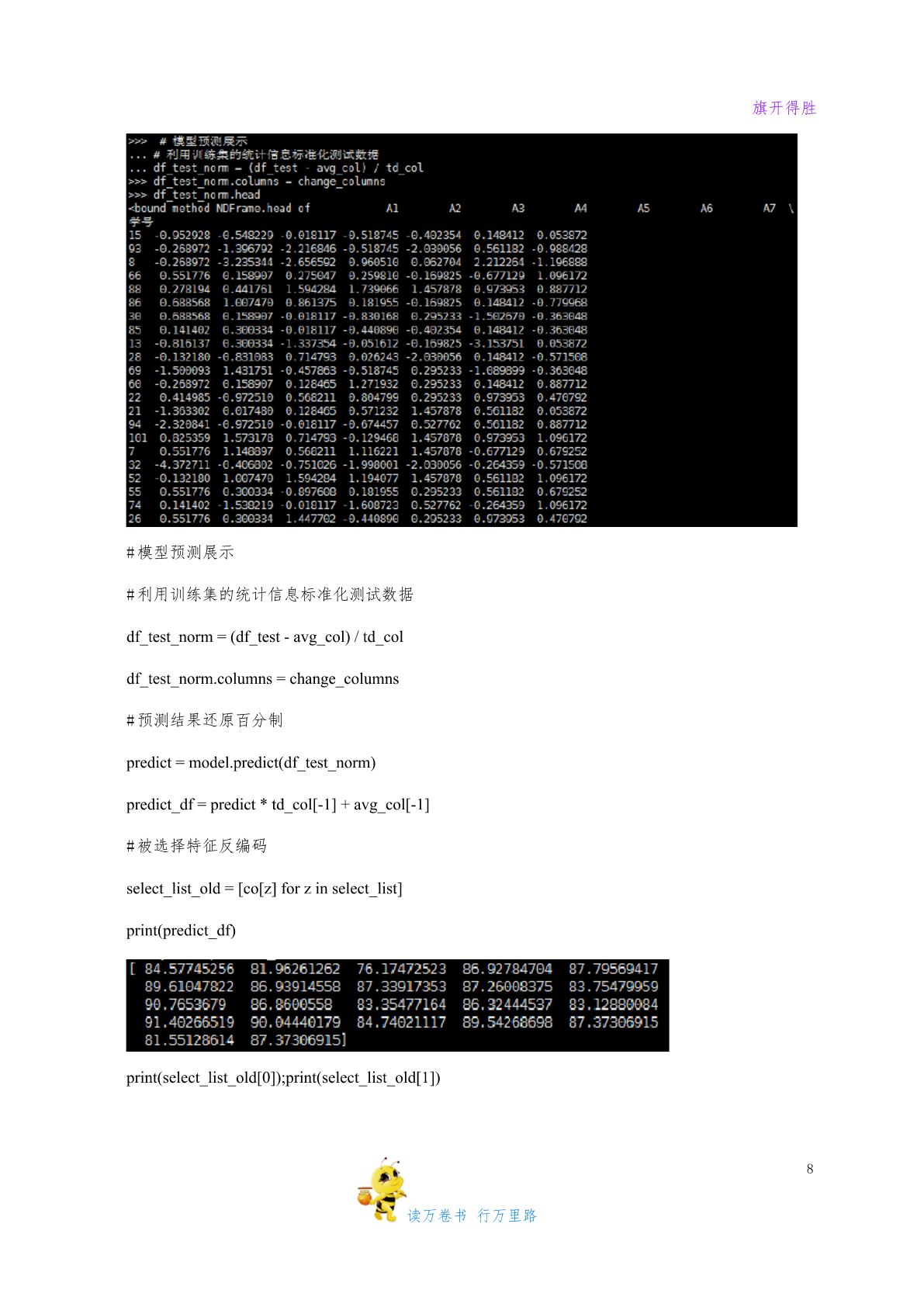
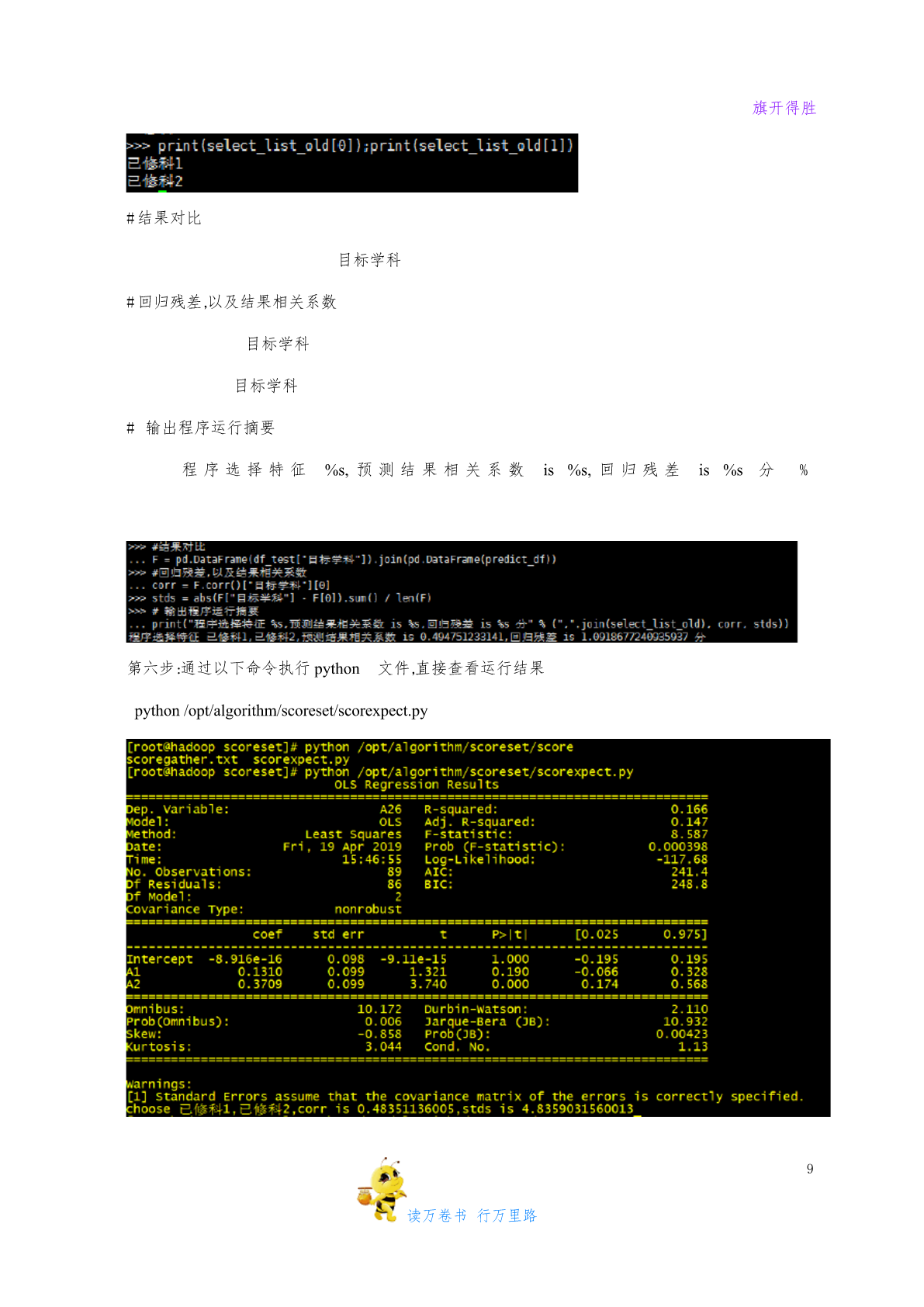
旗开得胜

实验算法python线性回归实验

【实验名称】

Python线性回归实验

【实验要求】

掌握Python线性回归模型应用过程，根据模型要求进行数据预处理，建模，评价与应用；

【背景描述】

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一

种统计分析方法，运用十分广泛。其表达形式为y=w'x+e，e为误差服从均值为0的正态分布。

【知识准备】

了解线性回归模型的使用场景，数据标准。了解Python/Spark数据处理一般方法。了解spark

模型调用，训练以及应用方法

【实验设备】

Windows或Linux操作系统的计算机。部署Python，本实验提供centos6.8环境。

【实验说明】

采用成绩数据集作为算法数据，对模型进行训练和回归。

【实验环境】

Pyrhon3.X，实验在命令行python中进行，或者把代码写在py脚本，由于本次为实验，以学

习模型为主，所以在命令行中逐步执行代码，以便更加清晰地了解整个建模流程。

【实验步骤】

第一步：启动python：

命令行键入python,启动python终端

第二步：导入用到的包，并读取数据：

1

读万卷书行万里路
旗开得胜

(1).导入包:

importnumpyasnp

importpandasaspd

importstatsmodels.formula.apiassmf

importscipy

(2).读取数据并随机打乱,文件路径为:/opt/algorithm/scoreset/scoregather.txt

rac=1)

(3).展示数据

df.head()

第三步：数据预处理

说明,数据集包含25门已修学科,以及一门目标学科

(1).划分训练集,测试集

PP=0.8

df_train=df.iloc[:int(np.ceil(len(df)*PP))]

df_test=df.iloc[int(np.ceil(len(df)*PP)):]

2

读万卷书行万里路
旗开得胜

(2).数据标准化,获取每列均值,标准差

avg_col=df_train.mean()

td_col=df_train.std()

(3).标准化结果

df_train_norm=(df_train-avg_col)/td_col

df_train_norm.head()

第四步：特征提取及线性回归模型训练

基于F检验的特征选择

(1).由于建模需要标准化字符串,故需重命名表头

list_columns_to_train=df_train_norm.columns

3

读万卷书行万里路
旗开得胜

change_columns=['A'+str(zr+1)forzrinnp.arange(len(list_columns_to_train))]

df_train_norm.columns=change_columns

co=dict(zip(change_columns,list_columns_to_train))

defR_transform(data=[],k=0):

r_L=data[k][k]

shape=np.mat(data).shape

R_t=np.zeros(shape)

foriinnp.arange(shape[0]):

forjinnp.arange(shape[1]):

if(i==k)&(j!=k):

R_t[i][j]=data[k][j]/r_L

elif(i!=k)&(j==k):

R_t[i][j]=-1*data[i][k]/r_L

elif(i==k)&(j==k):

R_t[i][j]=1.0/r_L

elif(i!=k)&(j!=k):

R_t[i][j]=data[i][j]-data[i][k]*data[k][j]/r_L

returnR_t

remaining=list(data.columns)

n=len(data)

#因变量选择列

4

读万卷书行万里路
旗开得胜

selected=[]

l=len(selected)

#计算相关系数矩阵

corr_R=data.corr()

mark=1

while(mark):

#首次变量选择

ifl!=(len(data.columns)-1):

r_taget=pd.Series(np.diagonal(np.mat(corr_R)))

r_taget.index=remaining

Vi=corr_R[response]**2/