
2_贝叶斯决策理论.pptx

和蔼****娘子









亲,该文档总共89页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

2_贝叶斯决策理论.pptx
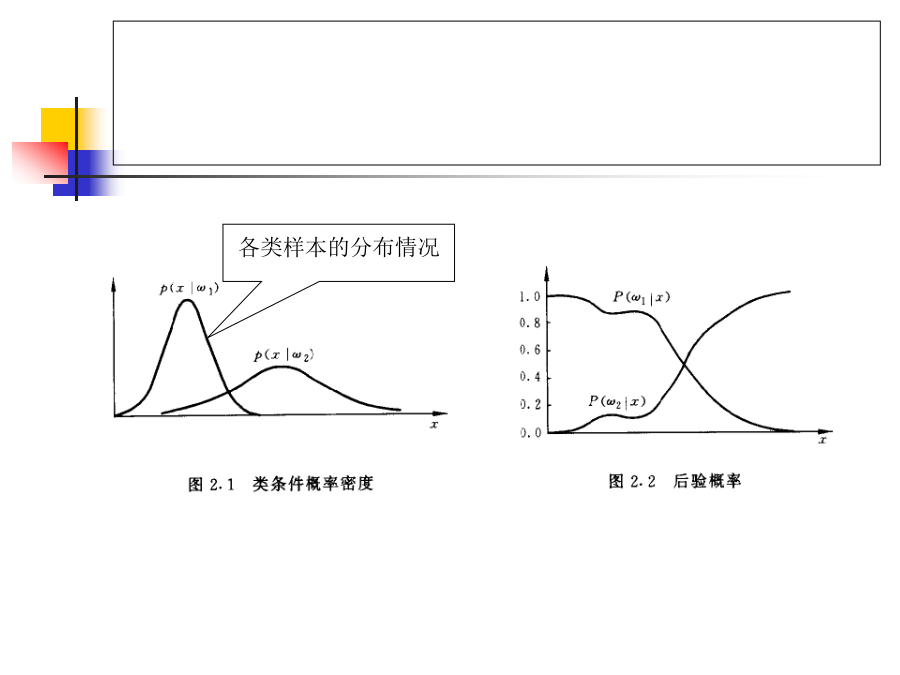
第2章贝叶斯决策理论2.1引言作为统计判别问题的模式分类但在现实世界中,由许多客观现象的发生,就每一次观察和测量来说,即使在基本条件保持不变的情况下也具有不确定性只有在大量重复的观察下,其结果才能呈现出某种规律性,即对它们观察到的特征具有统计特性特征值不是一个确定的向量,而是一个随机向量此时,只能利用模式集的统计特性来分类,以使分类器发生错误的概率最小统计识别的基本方法——贝叶斯决策2.2几种常用的决策规则2.2.1基于最小错误率的贝叶斯决策贝叶斯决策的出发点贝叶斯公式贝叶斯决策的几种表达形式两类模式集分

2_贝叶斯决策理论.ppt
第2章贝叶斯决策理论2.1引言作为统计判别问题的模式分类但在现实世界中,由许多客观现象的发生,就每一次观察和测量来说,即使在基本条件保持不变的情况下也具有不确定性只有在大量重复的观察下,其结果才能呈现出某种规律性,即对它们观察到的特征具有统计特性特征值不是一个确定的向量,而是一个随机向量此时,只能利用模式集的统计特性来分类,以使分类器发生错误的概率最小统计识别的基本方法——贝叶斯决策2.2几种常用的决策规则2.2.1基于最小错误率的贝叶斯决策贝叶斯决策的出发点贝叶斯公式贝叶斯决策的几种表达形式两类模式集分

关于贝叶斯决策理论.ppt
课前思考学习指南学习指南2.1引言物理对象的描述贝叶斯决策理论方法讨论的问题基于最小错误率的贝叶斯决策基于最小风险的贝叶斯决策在限定一类错误率条件下使另一类错误率为最小的两类别决策最小最大决策序贯分类方法2.2.1基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策条件概率几个重要概念贝叶斯决策理论基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基

关于贝叶斯决策理论.pptx
课前思考学习指南学习指南2.1引言物理对象的描述贝叶斯决策理论方法讨论的问题基于最小错误率的贝叶斯决策基于最小风险的贝叶斯决策在限定一类错误率条件下使另一类错误率为最小的两类别决策最小最大决策序贯分类方法2.2.1基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策条件概率几个重要概念贝叶斯决策理论基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基于最小错误率的贝叶斯决策基

贝叶斯决策-贝叶斯决策例题讲解.docx
贝叶斯决策:贝叶斯决策例题讲解3.贝叶斯决策张朝晖zhangzhaohui_hbsd@163.com河北师范大学数学与信息科学学院2011.7.29主要内容二.最小错误率贝叶斯决策三.最小风险的贝叶斯决策四.应用模式识别的分类(状态决策)问题:根据识别对象的特征观测,将其划分到某类别统计模式识别:用概率统计的观点和方法来解决模式识别问题贝叶斯决策论(统计决策理论):是统计模式识别的基本方法和基础;利用概率的不同,进行分类决策、或决策代价折衷;----“最优分类器”几个基本概念:[1]特征空间及特征维数:d
