
241圆的有关性质(第2课时).ppt

dc****76







亲,该文档总共14页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

圆的有关性质(第2课时).ppt
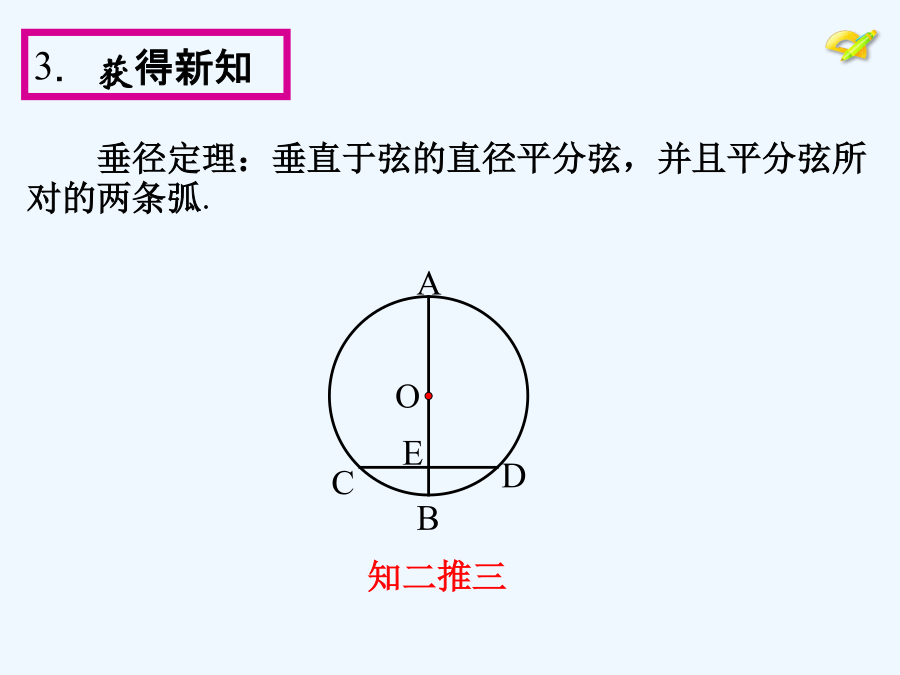
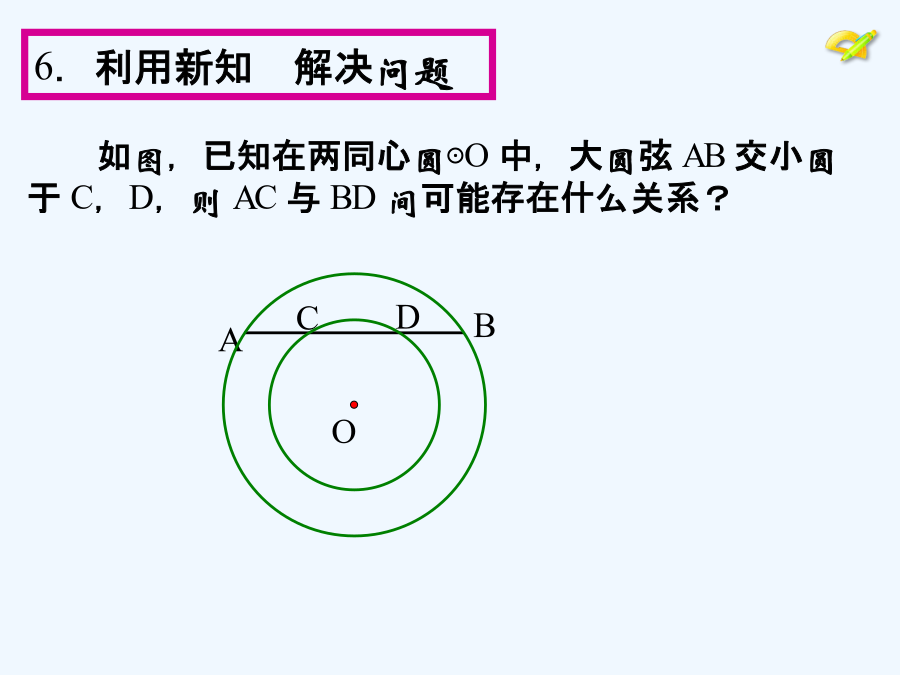
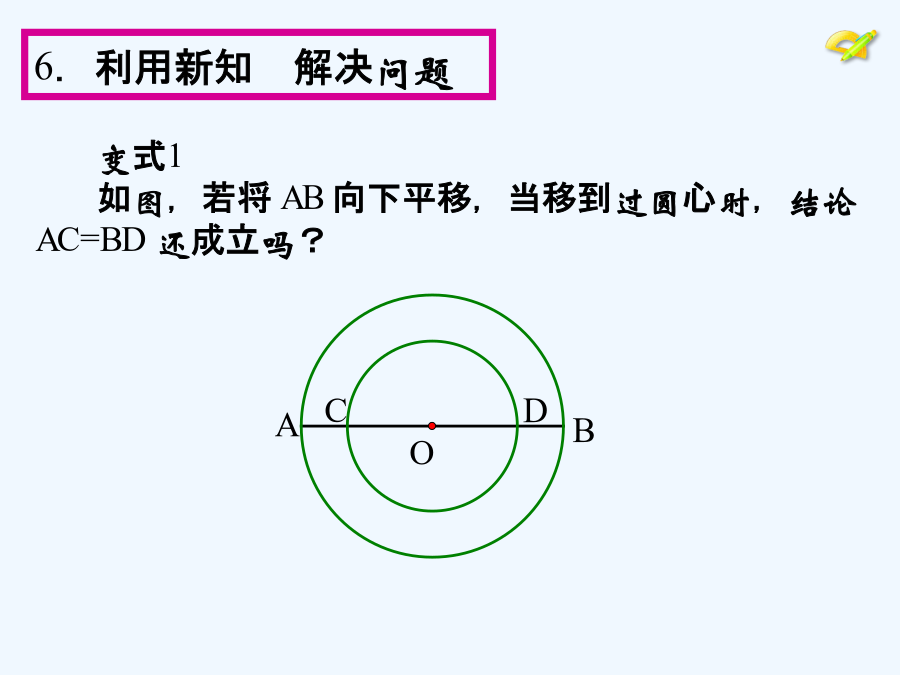
24.1圆的有关性质(第2课时)本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.学习目标:1.理解圆的轴对称性,会运用垂径定理解决有关的证明、计算和作图问题;2.感受类比、转化、数形结合、方程等数学思想和方法,在实验、观察、猜想、抽象、概括、推理的过程中发展逻辑思维能力和识图能力.学习重点:垂径定理及其推论.如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7

241 圆的有关性质(第2课时).ppt
24.1圆的有关性质(第2课时)本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.学习目标:1.理解圆的轴对称性,会运用垂径定理解决有关的证明、计算和作图问题;2.感受类比、转化、数形结合、方程等数学思想和方法,在实验、观察、猜想、抽象、概括、推理的过程中发展逻辑思维能力和识图能力.学习重点:垂径定理及其推论.如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7

241 圆的有关性质(第2课时).ppt
24.1圆的有关性质(第2课时)本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.学习目标:1.理解圆的轴对称性,会运用垂径定理解决有关的证明、计算和作图问题;2.感受类比、转化、数形结合、方程等数学思想和方法,在实验、观察、猜想、抽象、概括、推理的过程中发展逻辑思维能力和识图能力.学习重点:垂径定理及其推论.如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7

241圆的有关性质(第2课时).ppt
24.1圆的有关性质(第2课时)本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.学习目标:1.理解圆的轴对称性,会运用垂径定理解决有关的证明、计算和作图问题;2.感受类比、转化、数形结合、方程等数学思想和方法,在实验、观察、猜想、抽象、概括、推理的过程中发展逻辑思维能力和识图能力.学习重点:垂径定理及其推论.如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7

241 圆的有关性质(第2课时).ppt
24.1圆的有关性质(第2课时)本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.学习目标:1.理解圆的轴对称性,会运用垂径定理解决有关的证明、计算和作图问题;2.感受类比、转化、数形结合、方程等数学思想和方法,在实验、观察、猜想、抽象、概括、推理的过程中发展逻辑思维能力和识图能力.学习重点:垂径定理及其推论.如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7
