
教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar

醉香****mm



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar
1课题课时1课型新授课教学目标重点难点分析及突破措施教学重点:感受图形世界的丰富多彩,认识现实情境中的圆柱、圆锥、棱柱、棱锥、球。教学难点:运动的思想方法、圆柱、圆锥、球由旋转而形成突破措施:强化训练独立思考——合作交流法.板书设计1.1生活中的立体图形(1)1.面面相交得到线,线线相交得到点。2.图形的构成元素:点、线、面3.旋转体1.1生活中的立体图形教学过程上课时间:(包括导引新课、依标导学、异步教学、达标测试、作业设计等)一、创设情
教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar
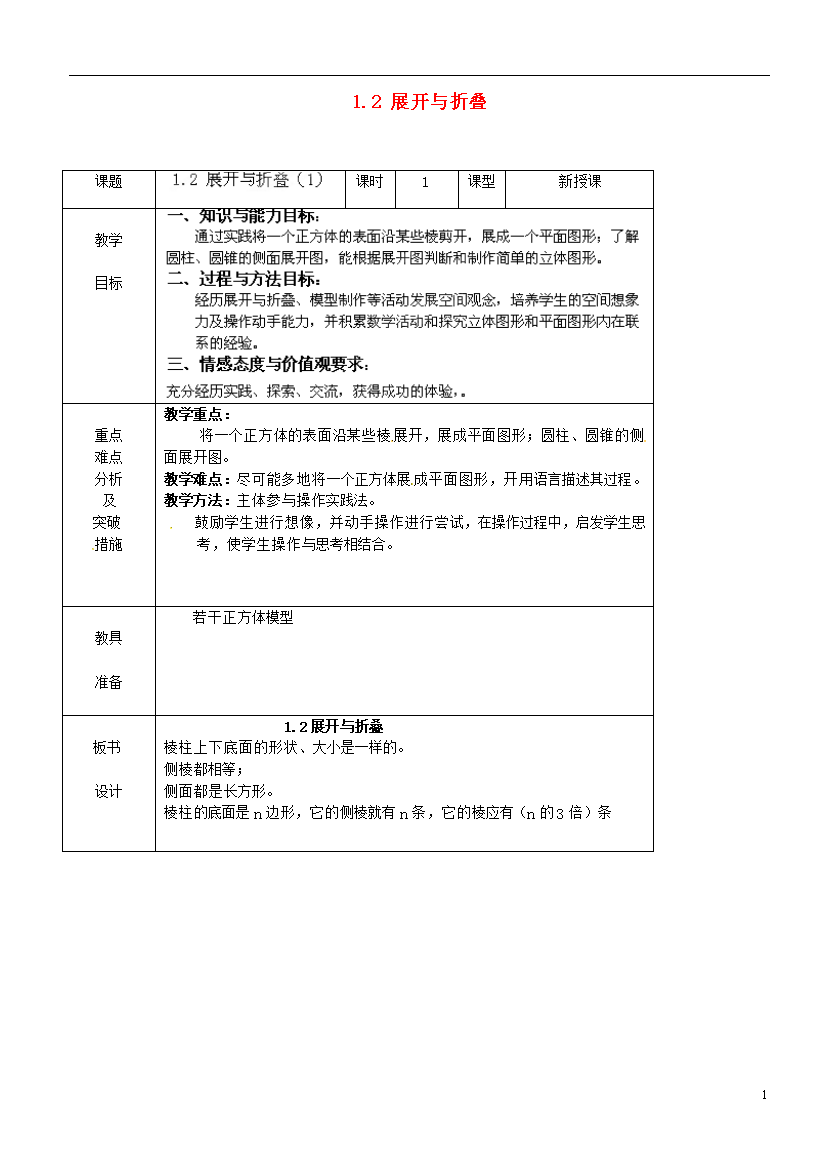
1课题课时1课型新授课教学目标重点难点分析及突破措施教学重点:将一个正方体的表面沿某些棱展开,展成平面图形;圆柱、圆锥的侧面展开图。教学难点:尽可能多地将一个正方体展成平面图形,开用语言描述其过程。教学方法:主体参与操作实践法。鼓励学生进行想像,并动手操作进行尝试,在操作过程中,启发学生思考,使学生操作与思考相结合。教具准备若干正方体模型板书设计1.2展开与折叠棱柱上下底面的形状、大小是一样的。侧棱都相等;侧面都是长方形。棱柱的底面是n边

教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar
11.1生活中的立体图形课题课时1课型新授课教学目标重点难点分析及突破措施教学重点:如何让学生自己用比较准确的数学语句来描述几何体中的点、线、面关系教学难点:用比较准确的数学语句来描述棱柱和圆柱体的相同点和不同点突破措施:强化训练独立思考——合作交流法.教具准备板书设计1.1生活中的立体图形(1)1、认识几何体2、认识棱柱3、圆柱与棱柱的相同点和不同点教学过程上课时间:(包括导引新课、依标导学、异步教学、达标测试、作业设计等)一、

教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar
11.4从不同方向看物体的形状课题课时1课型讲评课教学目标一、知识与能力目标:能识别简单物体的三视图,会画立方体及其简单组合体的三视图。二、过程与方法目标:(1)经历从不同方向观察物体的活动过程,发展空间观念;(2)在与其他人交流的过程中,能合理清晰地表达自己的思维过程;(3)在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形。三、情感态度与价值观:(1)通过创设问题情境,让学生主动参与,做“数学实验”,激发学生学习的热情和兴趣,激活学生思维。(2)在

教案-山东-2015_山东省龙口市诸由观镇诸由中学六年级数学上册 1.rar
1教学目标重点难点分析及突破措施教学重点:引导学生经历用一个平面去截一个正方体的切截活动过程,体会截面和几何体的关系,充分让学生动手操作、自主探索、合作交流。教学难点:1.从切截活动中发现规律,并能用自己的语言合理清晰地来表达出自己的思维过程。2.能应用规律来解决问题,从理论上理解截出五边形、六边形的可能性,以及七边形的不可能性。教学方法:1、观察猜想2、合作交流3、操作实验教具准备若干模型板书设计1.3截一个几何体1、用一个平面截一个正方体得
