电动力学七四(切伦柯夫辐射).ppt

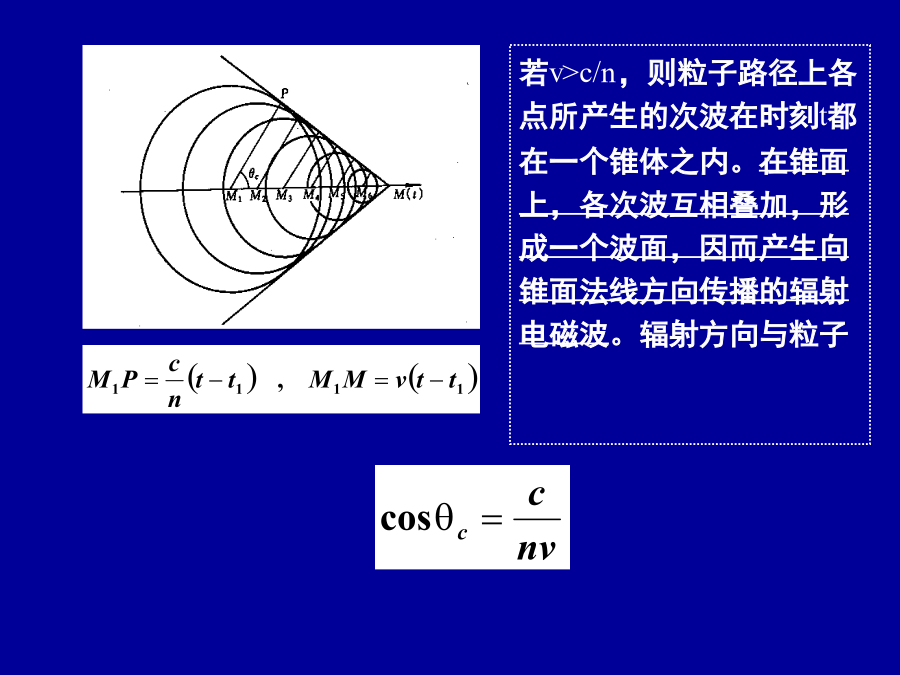
四、切伦柯夫(Cerenkov)辐射切伦柯夫辐射的物理机制若v>c/n，则粒子路径上各点所产生的次波在时刻t都在一个锥体之内。在锥面上，各次波互相叠加，形成一个波面，因而产生向锥面法线方向传播的辐射电磁波。辐射方向与粒子运动方向的夹角c由下式确定，由于切伦柯夫辐射是运动带电粒子与介质内的束缚电荷和诱导电流所产生的集体效应，而在宏观现象中，介质内束缚电荷和诱导电流分布产生的宏观效应可以归结为电容率和磁导率，因此在研究切伦柯夫辐射时，可以对介质作宏观描述，即用和两参量来描述介质。为简单起见，先假设和是不依赖于频率的常量，并设=0，因而介质内的光速为c/n＝c(r)-1/2，其中n为介质的折射率，r为相对电容率。当n为常数时，介质内的标势和矢势方程为设粒子以匀速v作直线运动，其位矢为x=xe(t)=vt，它的电荷密度和电流密度为用频谱分析方法求解K=(/c)n为介质中波数因为n与A的夹角为，所以B的量值为因此若粒子运动速度v>c/n，在cos=c/nv方向上书B变为无穷大，因此在这方向上出现辐射电磁场。无穷大的出现是我们作了简化假设的结果。上面我们假设折射率n是与无关的常数，结果得到有一个确定的辐射角c，满足cosc=c/nv，在这单一辐射角下电磁场变为无穷大。用Sn=EH=()-1/2BH=(c/n)B2，可导出把其中一个因子变为函数。由于有这个函数因子，(1/v)-(n/c)cos能取=0，因此，另一个因子可写为最后一个因子是粒子所走的无穷大路程。这无穷大的出现也是我们作了简化假设的结果。事实上，粒子在介质中只走过有限的路程。当路程L>>辐射波长时，以上的计算仍然近似适用，但应代为L。粒子走过单位路程时的单位频率间隔辐射能量角分布如果考虑折射率对频率的依赖关系函数因子表示只有在cos=c/nv方向上才有辐射。单位路程单位频率间隔的辐射能量为图示仅在一定的频率范围内满足()>c2/v2，因此，切伦柯夫辐射的频谱只包含这一频段。由于cosc＝c/v。不同频率的电磁波的辐射角亦略有不同。用滤波器选择一定的频带，可以得到确定c的值，因而测定辐射角c就可以定出粒子的速度v。