直线与圆 视角最大问题——米勒定理.pdf

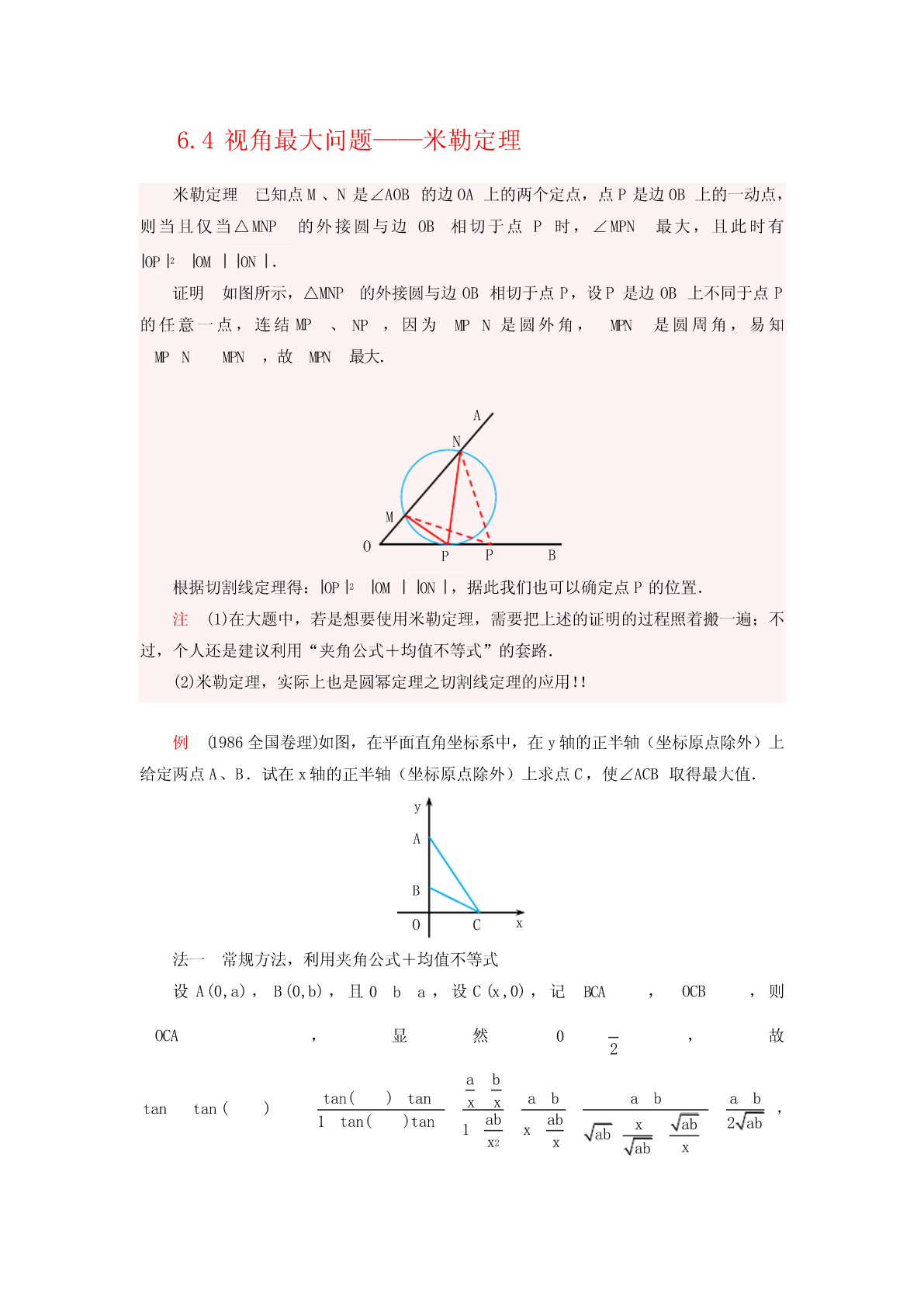
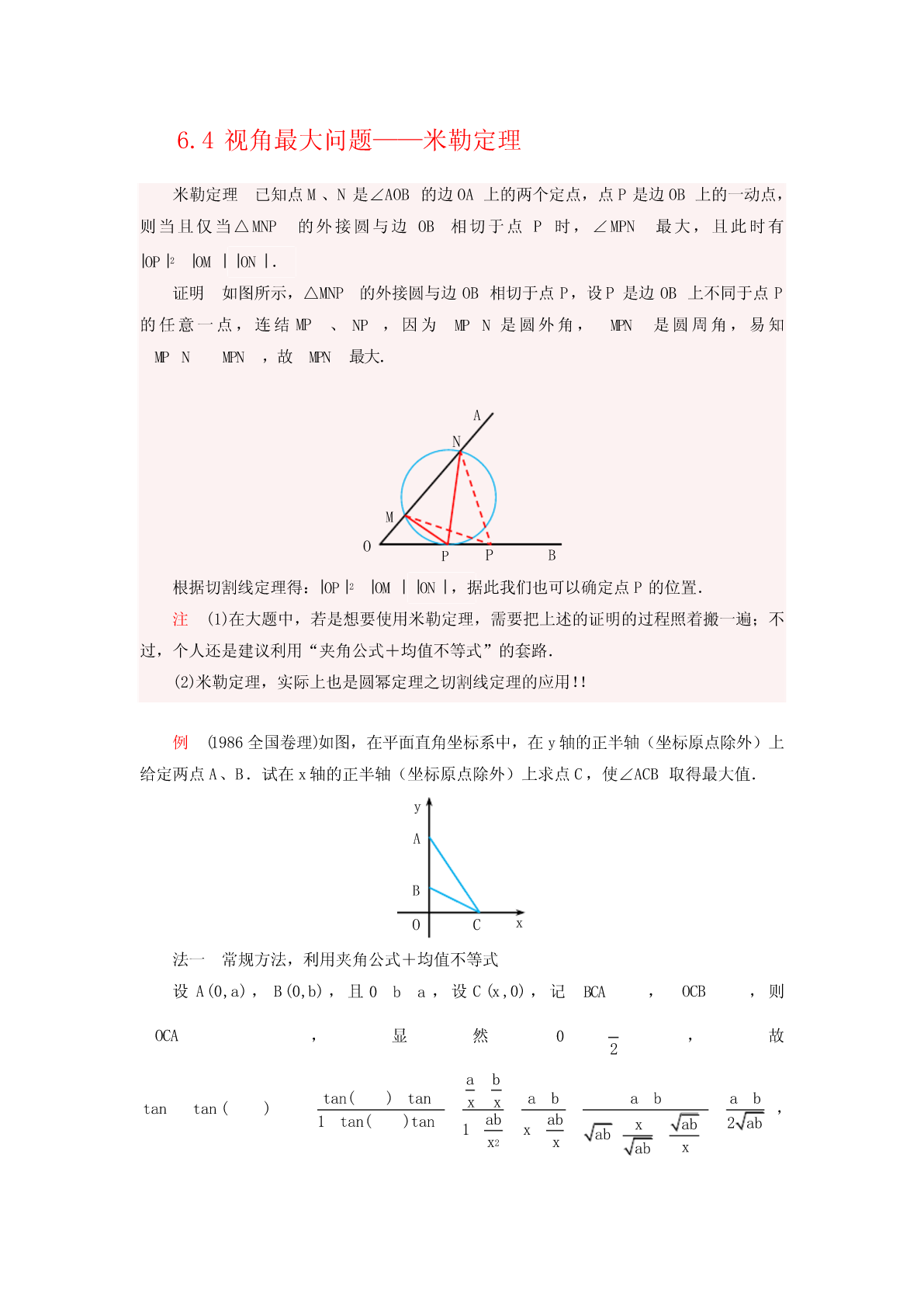
6.4视角最大问题——米勒定理米勒定理已知点M、N是∠AOB的边OA上的两个定点，点P是边OB上的一动点，则当且仅当△MNP的外接圆与边OB相切于点P时，∠MPN最大，且此时有OP2OMON．证明如图所示，△MNP的外接圆与边OB相切于点P，设P是边OB上不同于点P的任意一点，连结MP、NP，因为MPN是圆外角，MPN是圆周角，易知MPNMPN，故MPN最大．ANMOPPB根据切割线定理得：OP2OMON，据此我们也可以确定点P的位置．注(1)在大题中，若是想要使用米勒定理，需要把上述的证明的过程照着搬一遍；不过，个人还是建议利用“夹角公式＋均值不等式”的套路．(2)米勒定理，实际上也是圆幂定理之切割线定理的应用！！例(1986全国卷理)如图，在平面直角坐标系中，在y轴的正半轴（坐标原点除外）上给定两点A、B．试在x轴的正半轴（坐标原点除外）上求点C，使∠ACB取得最大值．yABOCx法一常规方法，利用夹角公式＋均值不等式设A(0,a)，B(0,b)，且0ba，设C(x,0)，记BCA，OCB，则OCA，显然0，故2abtan()tanabababtantan()xx，1tan()tanababxab2ab1xabx2xabxxabab当且仅当，即xab时，tan取得最大值，因此，当点C为(ab,0)时，abx2abab∠ACB取得最大值arctan．2ab法二利用米勒定理，显然，过点A、B的圆和x轴相切于点C时，∠ACB取得最大值，设OAa，OBb，此时OC2OAOB，即点C的坐标为(ab,0)．例(2005天津文理)某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC80(米)，塔所在的山高OB220(米)，OA200(米)，图中所示的山坡可视为直线l且1点P在直线l上，l与水平地面的夹角为a，tana．试问此人距水平地面多高时，观看塔2的视角BPC最大（不计此人的身高）．CBlPOAED解如图所示，延长PA交CO的延长线于点D，过点P作PE⊥OA于点E．易得ODOAtan100，AD1005．欲使得观看塔的视角BPC最大，则必有△PBC的外接圆与直线l相切于点P，根据切割线定理：DP2DBDC，即DP3204001605，从而PA605．1因此，PEPAsin60560，所以当此人距水平地面60米高时，观看塔的5视角BPC最大．例(2005浙江理)如图，已知椭圆的中心在坐标原点，焦点F、F在x轴上，长轴AA1212的长为4，左准线l与x轴的交点为M，MA：AF2：1．111(1)求椭圆的方程；(2)若直线l：xm(m1)，P为l上的动点，使FPF最大的点P记为Q，求点Q的1112坐标(用m表示)．ylPMAFOFAx1122l1x2y2略解(1)1；43(2)设直线l与x轴的交点为H，则点Q(m,y)，m1，则HQ2HFHF，即1012y2(1m)(1m)，即ym21，即点Q的坐标为(m,m21)，m1．QQ例(2010江苏)某兴趣小组要测量电视塔AE的高度H（单位：m）.如示意图，垂直放置的标杆BC的高度h4m，仰角ABE，ADE．(1)该小组已测得一组、的值，算出了tan1.24，tan1.20，请据此算出H的值；(2)该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使与之差较大，可以提高测量精度.若电视塔的实际高度为125m，试问d为多少时，最大？EEPQCCDADABdBdHtandtanHhtan解(1)由得：，即H124m；hHHhtanHhtantantanBDADd(2)HHhtantanhdhhtan()dd，HHh2H(Hh)1tantan1dH(Hh)d2H(Hh)ddd当且仅当dH(Hh)125121555时，tan()取得最大值．又0，则0，因此，当d555m时，最大．22背景本题实际上也是米勒定理的应用，不过稍微有点特殊，如果选择线段BD对应的视角∠BED进行分析，会发现BD是运动的，E是固定的，无法利用米勒定理，需要另寻他径进行转化．由于视角的对边是定值，注意到BC刚好为定值，因此，不妨选择BC为对边，同时延长CP，使得BPAE，根据相对运动可知：点E刚好在直线PQ上运动，此时，即可利用米勒定理，当且仅当过B、C的圆且与PQ相切于点E时，∠BEC取