
高级加密标准AES.ppt

含秀****66








亲,该文档总共60页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

高级加密标准AES.ppt
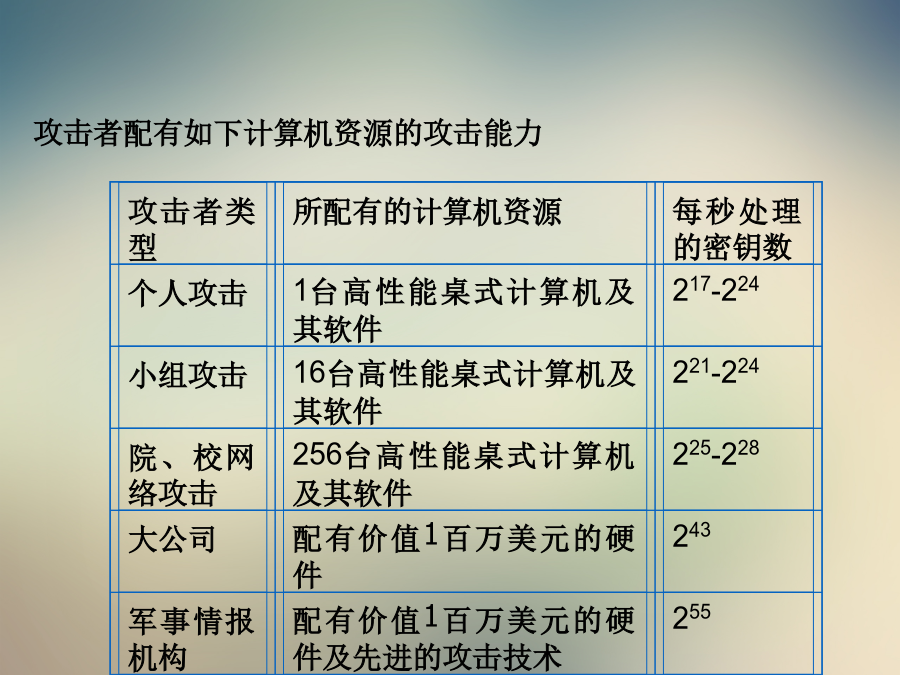
30六月2024攻击者类型1.AES的起源Rijndael(Raindoll)加密算法是分组长度可变、密钥长度也可变的分组密码。分组长度、密钥长度彼此独立地确定为128、192、256比特。AES的要求是比三重DES快而且至少和三重DES一样安全,分组长度为128比特,密钥长度为128/192/256比特。所以,AES和Rijndael是有差别的。分组长度(bit)设G为非空集合,在G内定义了一种代数运算,若满足下述公理:(1)有封闭性。对任意a、b∈G,恒有aοb∈G.(2)结合律成立。对任意a、b、c

高级加密标准AES.ppt
20十一月2024攻击者类型1.AES的起源Rijndael(Raindoll)加密算法是分组长度可变、密钥长度也可变的分组密码。分组长度、密钥长度彼此独立地确定为128、192、256比特。AES的要求是比三重DES快而且至少和三重DES一样安全,分组长度为128比特,密钥长度为128/192/256比特。所以,AES和Rijndael是有差别的。分组长度(bit)设G为非空集合,在G内定义了一种代数运算,若满足下述公理:(1)有封闭性。对任意a、b∈G,恒有aοb∈G.(2)结合律成立。对任意a、b、

高级加密标准(AES).ppt
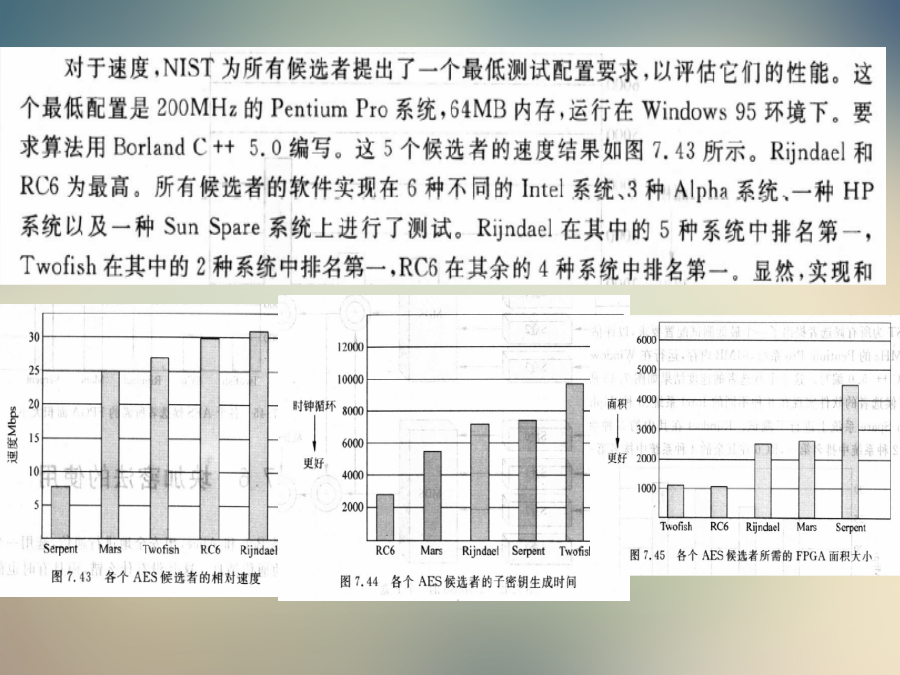
第5章高级加密标准(AES)1.AES的起源2.AES的设计原则分组长度(bit)3.AES算法的一般描述RijndaelRound的构成3.AES算法加密部分的实现0一些相关的的术语定义和表示Fig3.当Nb=6时的状态和Nk=4时的密钥布局Fig4.分组长度和密钥长度均为128bits时的Rijndael加密算法框图表2.轮数(Round)的不同取值用伪代码表示的Rijndael轮变换ByteSubstitution(字节替代)y011111000x00y101111100x11y200111110x

高级数据加密标准AES.ppt
高级数据加密标准提纲AESHistory高级数据加密标准AESAES应用AES数学基础AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AES数学基础(续)AE

高级数据加密标准AES讲义.pdf
