
结构位移计算.ppt

冬易****娘子







亲,该文档总共105页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

结构位移计算.ppt
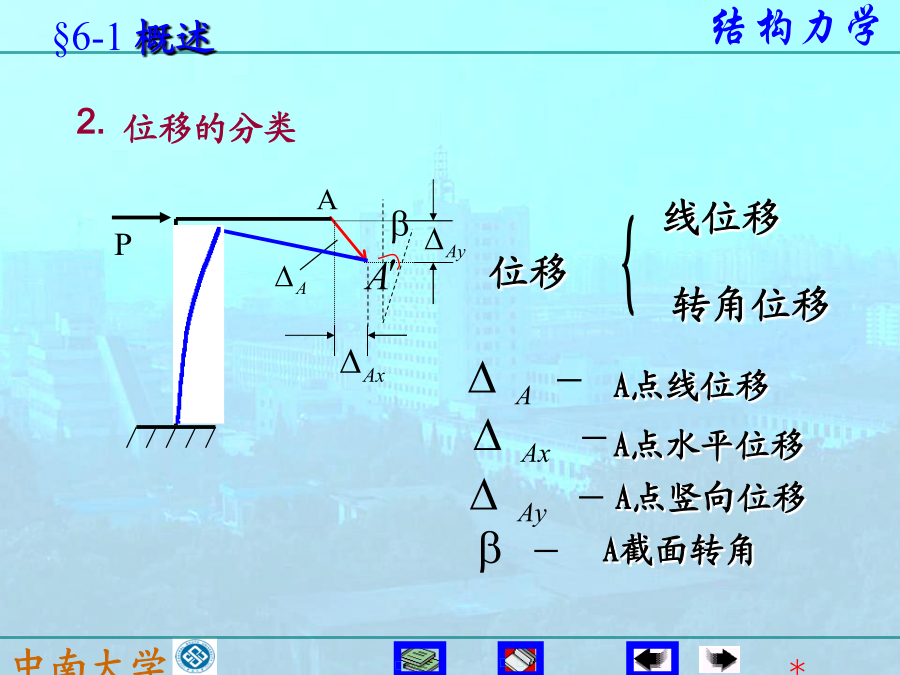
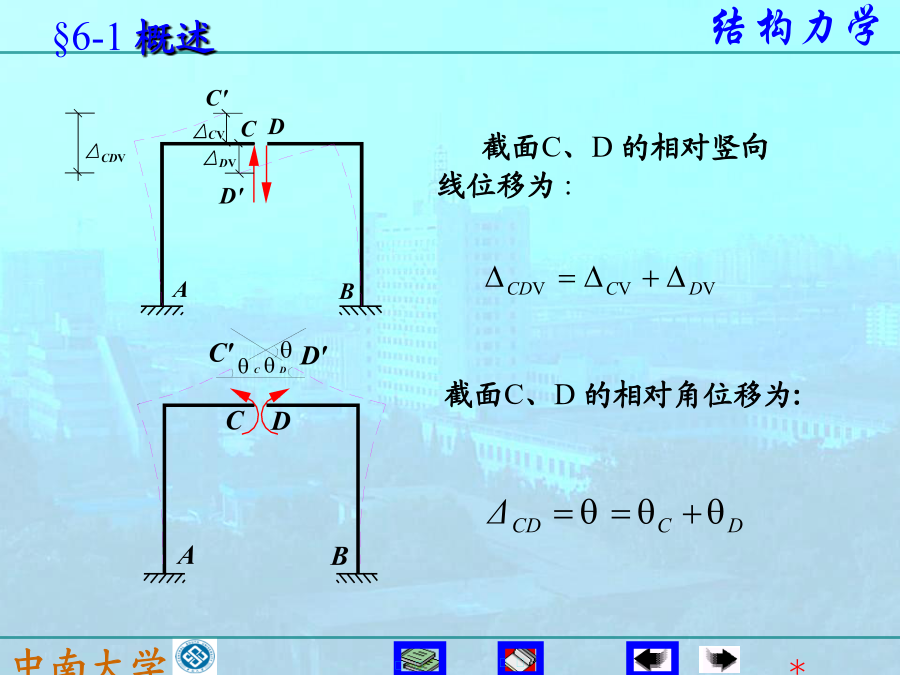
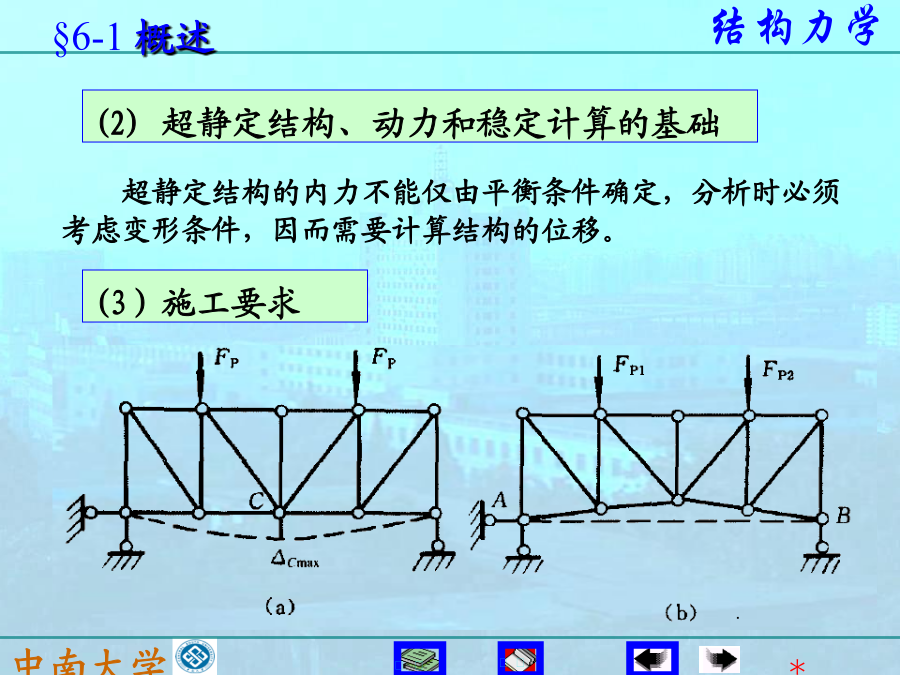
§6-1概述一、结构的位移(DisplacementofStructures)A截面C、D的相对竖向线位移为:A铁路工程技术规范规定:(2)超静定结构、动力和稳定计算的基础(3)理想联结(IdealConstraint)。本章只讨论应用虚功原理求解结构位移。一、基本概念实功的数值就等于图上三角形OAB的面积。实功是外力的非线形函数,计算外力实功不能应用叠加原理。2.外力的虚功力F1在力F2引起的位移Δ12上作的功为虚功为——结构产生的各种位移,包括截面的线位移、角位移、相对线位移、相对角位移或者是一组位移

结构位移计算.docx
第三章结构位移计算一、是非题(“是”打√,“非”打)1、增加各杆刚度,则结构的结点位移就一定减少。()2、引起结构变形的因素只有三种:荷载作用、温度改变和支座位移。()3、虚位移原理中的虚功方程等价于静力平衡方程,虚力原理中虚功方程等价于变形协调方程。()4、虚功原理适用于线性和非线性变形体系,但由此得到的荷载作用下结构位移计算公式只适用于线性变形体系。()5、有变形就有应力,有应力就有变形。()6、线性变形体受荷载、支座移动和温度变化作用的状态都满足功的互等定理。()7、由虚功方程推得的位移计算公式只适

结构位移计算.ppt
前面所学五种静定结构(梁,刚架,拱,桁架,组合结构)的内力计算可归结为强度问题,而结构力学的重要任务之一是解决刚度问题_结构位移计算.A′§6—1概述F4.计算结构位移的目的1)校核刚度——位移是否超过许用限值,防止构件和结构产生过大的变形而影响结构的正常使用。2)满足施工要求结构的变形(可能与正常使用时完全不同)。1.悬臂拼装架梁:正常使用时,最大挠度在跨中,施工时悬臂端B挠度最大,设计时考虑。3)解超静定问题平衡条件+变形协调条件(求结构的位移)4)结构动力计算的需要。功=力×力作用点沿其方向的位移d

结构位移计算.pptx

结构位移计算.ppt
§6-1概述一、结构的位移(DisplacementofStructures)A截面C、D的相对竖向线位移为:A铁路工程技术规范规定:(2)超静定结构、动力和稳定计算的基础(3)理想联结(IdealConstraint)。本章只讨论应用虚功原理求解结构位移。一、基本概念实功的数值就等于图上三角形OAB的面积。实功是外力的非线形函数,计算外力实功不能应用叠加原理。2.外力的虚功力F1在力F2引起的位移Δ12上作的功为虚功为——结构产生的各种位移,包括截面的线位移、角位移、相对线位移、相对角位移或者是一组位移
