
电力系统暂态能量函数法暂态稳定分析1.ppt

一吃****海逸







亲,该文档总共105页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

电力系统暂态能量函数法暂态稳定分析1.ppt
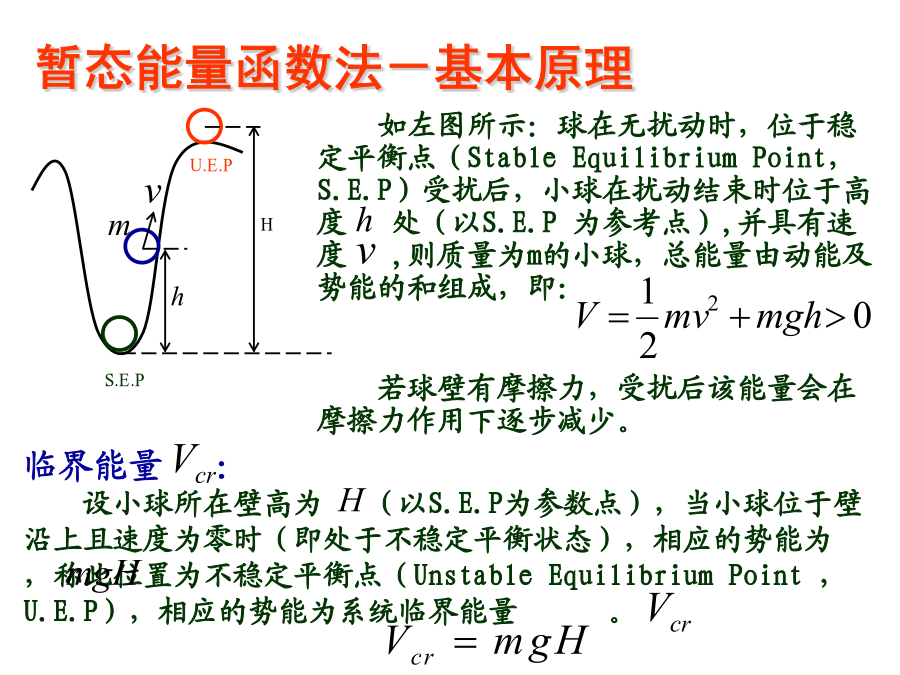
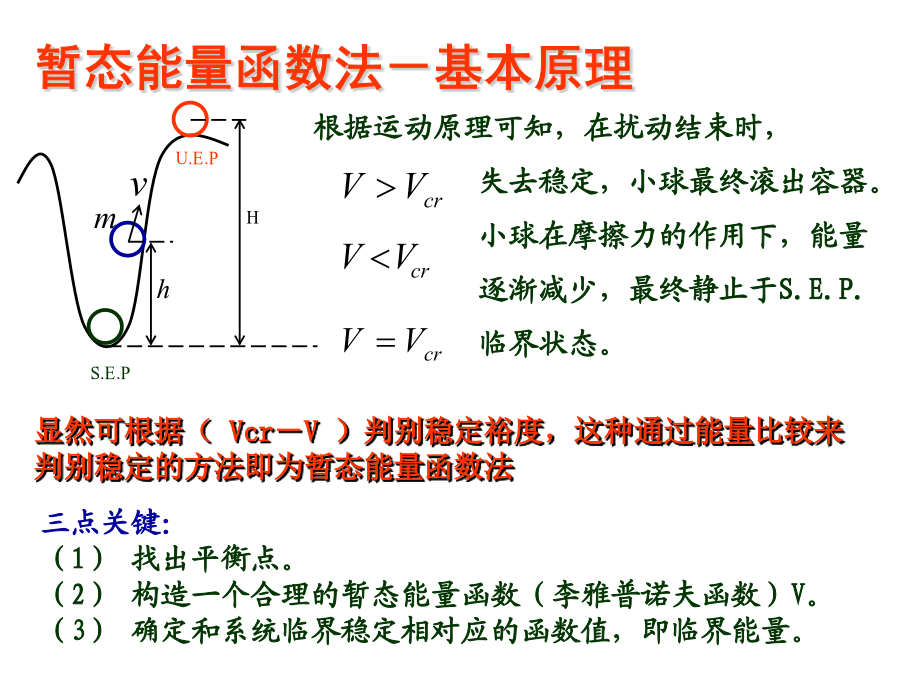
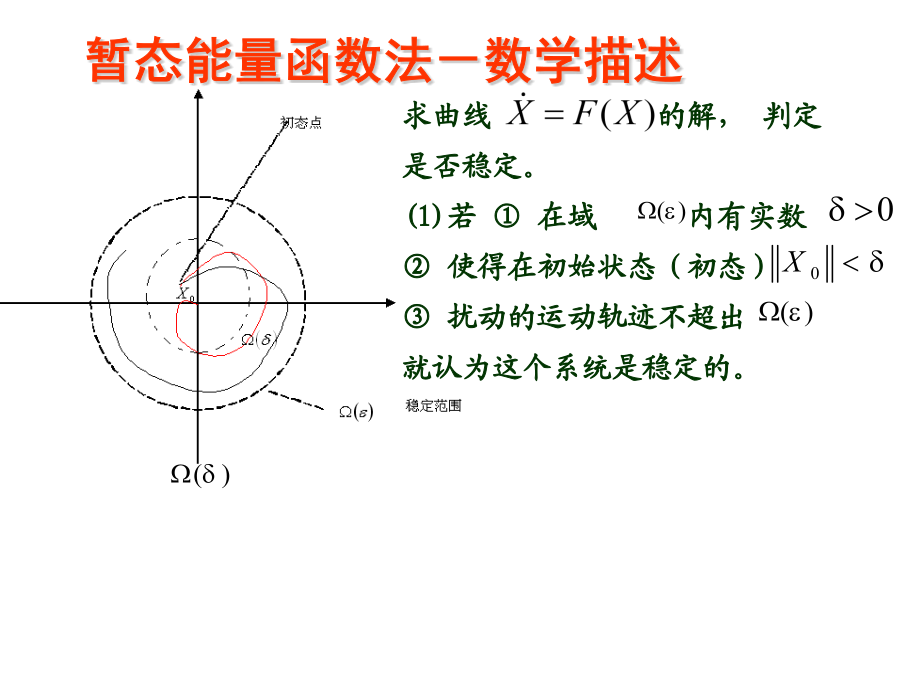
电力系统暂态能量函数法暂态稳定分析本章主要内容暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-数学描述2)在内出发的运动,在不能限定在内,则不稳定。3)在内出发的运动,无限接近坐标原点,称之为渐近稳定。4)只有当初态点在某一区域,系统才是渐近稳定的,这个区域称之为引力域。1)状态变量X的运动方程2)稳定平衡点取作坐标原点3)在坐标原点附近存在一标量函数当时,当时,4)若,,则系统稳定,但不一定回到原点(稳定平衡点)。5)若,,则渐近稳定,一定会回到原点。6)初态点在

电力系统暂态能量函数法暂态稳定分析1.ppt
电力系统暂态能量函数法暂态稳定分析本章主要内容暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-数学描述2)在内出发的运动,在不能限定在内,则不稳定。3)在内出发的运动,无限接近坐标原点,称之为渐近稳定。4)只有当初态点在某一区域,系统才是渐近稳定的,这个区域称之为引力域。1)状态变量X的运动方程2)稳定平衡点取作坐标原点3)在坐标原点附近存在一标量函数当时,当时,4)若,,则系统稳定,但不一定回到原点(稳定平衡点)。5)若,,则渐近稳定,一定会回到原点。6)初态点在

电力系统暂态能量函数法暂态稳定分析.pptx
会计学本章主要内容暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-基本原理暂态能量函数法-数学描述2)在内出发的运动,在不能限定在内,则不稳定。3)在内出发的运动,无限接近坐标原点,称之为渐近稳定。4)只有当初态点在某一区域,系统才是渐近稳定的,这个区域称之为引力域。1)状态变量X的运动方程2)稳定平衡点取作坐标原点3)在坐标原点附近存在一标量函数当时,当时,4)若,,则系统稳定,但不一定回到原点(稳定平衡点)。5)若,,则渐近稳定,一定会回到原点。6)初态点在一定范围,才满足,则这个域称

暂态能量函数法暂态稳定分析学习教案.pptx
会计学仿真(fǎnɡzhēn)法的缺点/电力系统暂态能量(néngliàng)函数法TEF单机无穷大系统(xìtǒng)的直接法单机无穷大系统(xìtǒng)的相平面图向多机系统扩展(kuòzhǎn)的三种思路多机系统直接(zhíjiē)法稳定分析同步(tóngbù)坐标下的TEF与Vcr/惯量中心(zhōngxīn)COI坐标下的TEF和Vcr/部分(bùfen)惯量中心PCOI坐标下的TEF单机无穷大等值RUEP暂态稳定(wěndìng)分析PEBS暂态稳定(wěndìng)分析//综合法直接(zhí

暂态分析-电力系统暂态稳定分析.pdf
第七章电力系统暂态稳定分析20082008年年66月月99日日第七章电力系统暂态稳定分析§7-1概述§7-2简单电力系统的暂态稳定性§7-3自动调节系统对暂态稳定的影响§7-4复杂电力系统的暂态稳定性§7-5提高暂态稳定性的措施§7-1概述一.定义二.分析方法三.分析假定四.稳定一般条件§7-1概述一.定义电力系统突然受到大的干扰后,能否恢复到原来的运行状态或达到新的稳态运行状态的能力。大干扰是相对于静态稳定分析中所的小干扰言,一般指短路故障,变压器、线路突然断开或切除发电机等。正常操作范围的元件投切,应
