预览加载中，请您耐心等待几秒...

利用勾股定理解决图形折叠和求图形面积的问题.ppt

预览
1/9
2/9
3/9
4/9
5/9
6/9
7/9
8/9
9/9

在线预览结束，喜欢就下载吧，查找使用更方便

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

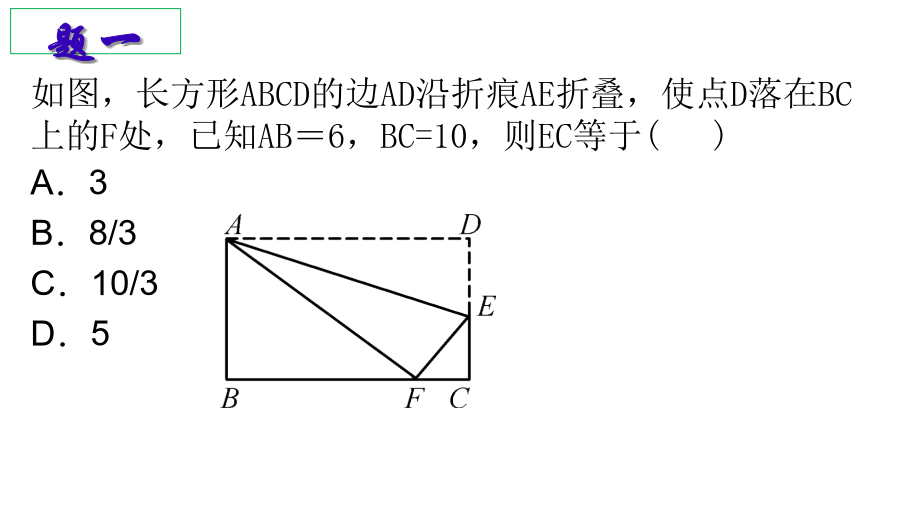
利用勾股定理解决图形 折叠和求图形面积的问题 （1）折叠问题的变与不变，变的是折叠前后图形的位置，不变的是折叠前后图形的形状和大小，因此折叠前后的两个图形是全等的，进而可以利用全等的性质求解。（1）折叠问题的变与不变，变的是折叠前后图形的位置，不变的是折叠前后图形的形状和大小，因此折叠前后的两个图形是全等的，进而可以利用全等的性质求解。（1）折叠问题的变与不变，变的是折叠前后图形的位置，不变的是折叠前后图形的形状和大小，因此折叠前后的两个图形是全等的，进而可以利用全等的性质求解。题一在长方形ABCD中，BC＝6，CD＝3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为() A．3 B.15/4 C．5 D.15/2 在Rt△ABC中，∠C＝90°，BC＝6cm，AC＝8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是()． 总结：总结：