一种RS码编码参数的盲识别方法.pdf

(19)中华人民共和国国家知识产权局(12)发明专利(10)授权公告号(10)授权公告号CNCN102201883102201883B(45)授权公告日2014.08.13(21)申请号201010131104.8thepresenceofintersymbolinterference.(22)申请日2010.03.23《IEEE/IEEElectronicLibrary(IEL)数据库》.2001,全文.(73)专利权人中国电子科技集团公司第三十六刘健，谢锘，周希元.RS码的盲识别方法.《电研究所子科技大学学报》.2009,第38卷(第3期),全地址314033浙江省嘉兴9号信箱文.(72)发明人张永光楼财义审查员袁锦波(74)专利代理机构上海航天局专利中心31107代理人郑丹力(51)Int.Cl.H04L1/00(2006.01)H03M13/15(2006.01)(56)对比文件CN1713559A,2005.12.28,全文.CN101534168A,2009.09.16,全文.KazuoTanada,HiroshiKubo,AkihiroOkazaki,TakeshiUraguchi.ExperimentalevaluationofaparallelblinddemodulatorcombinedwithaReed-Solomondecoderin权权利要求书1页利要求书1页说明书5页说明书5页附图3页附图3页(54)发明名称一种RS码编码参数的盲识别方法(57)摘要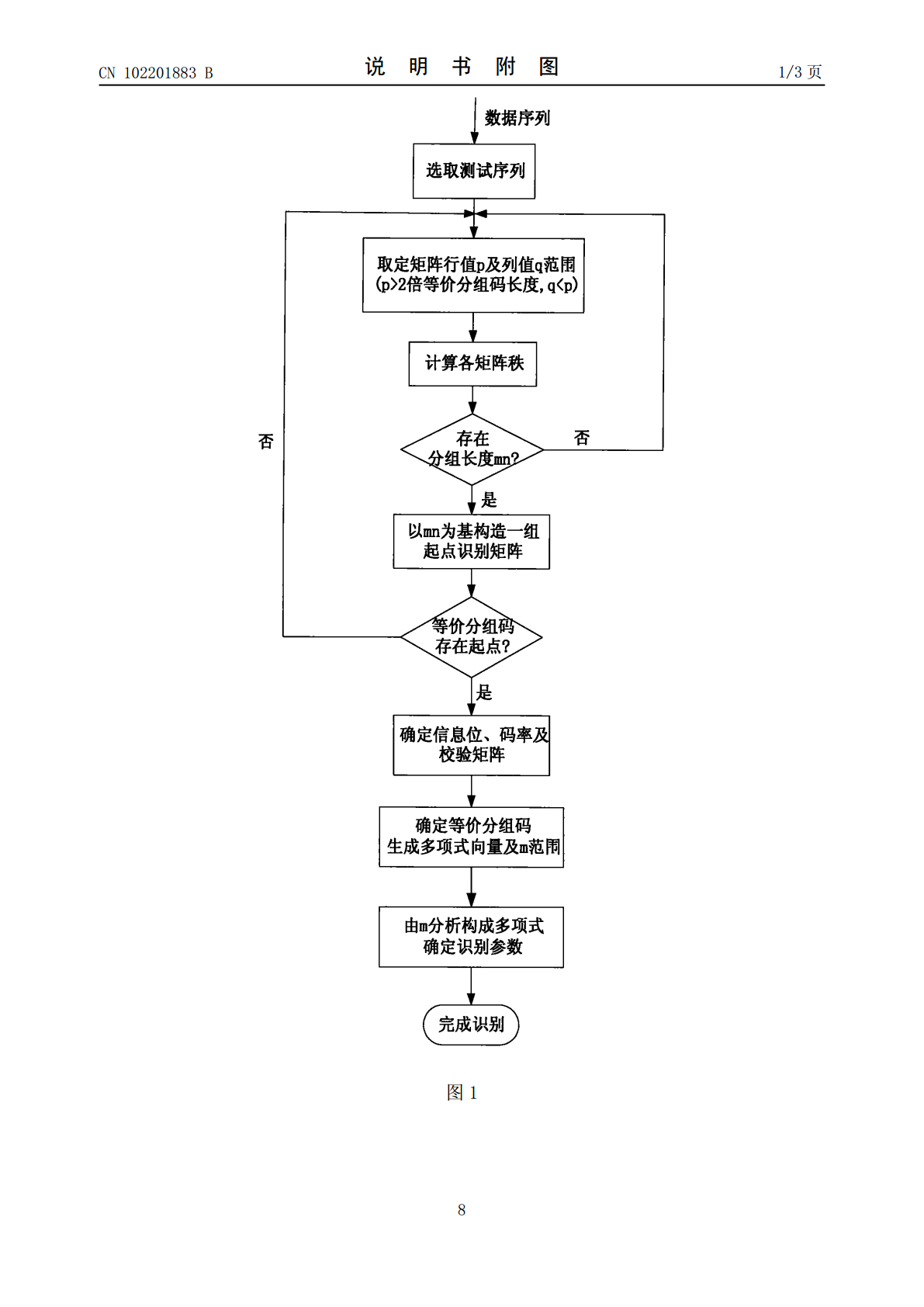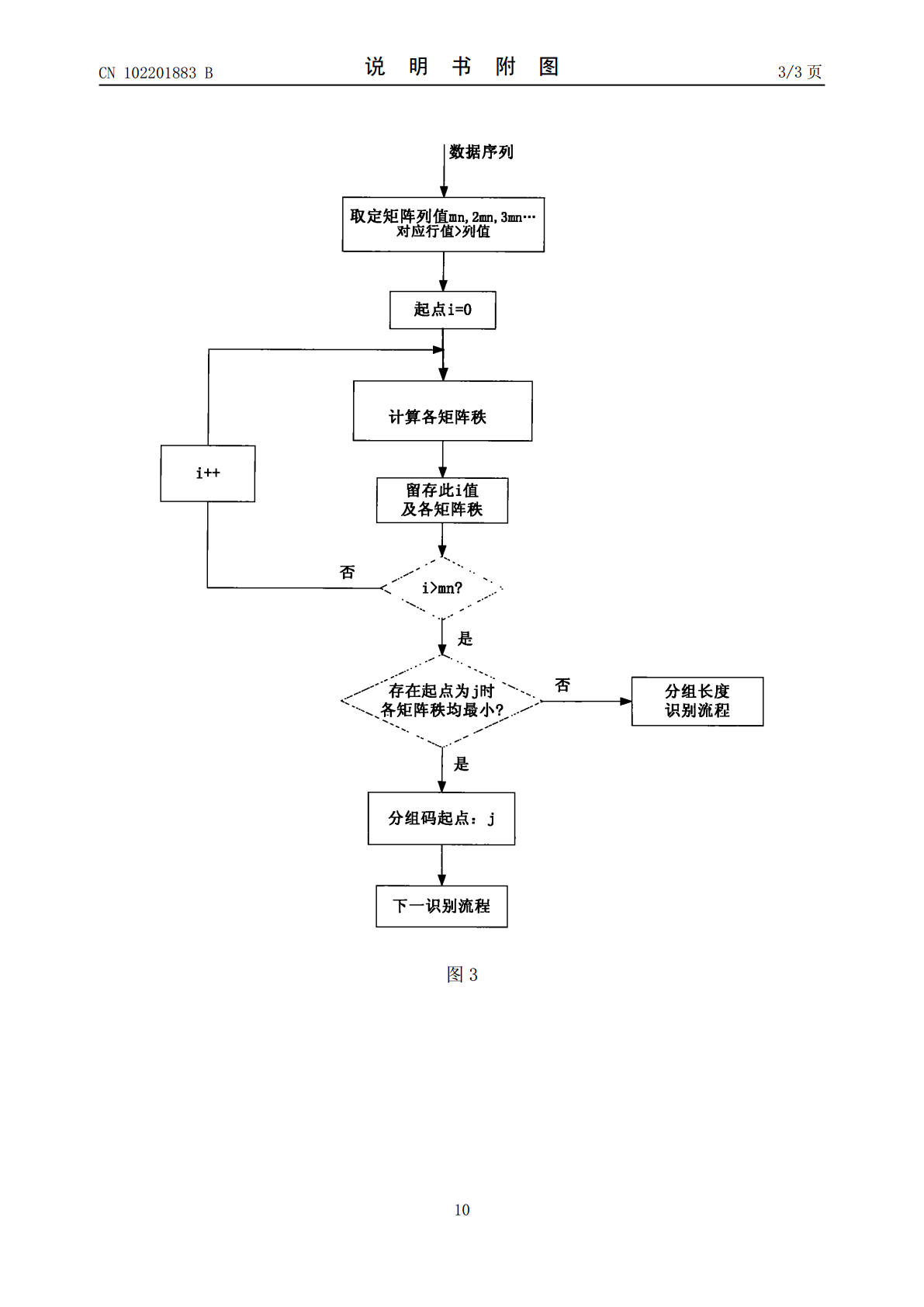本发明公开了一种RS码编码参数的盲识别方法。该方法在分阶段确定其等价二进制线性分组码的分组长度和分组起点后，对矩阵进行变换，确定其等价分组码的校验矩阵，通过符号数m，进而确定分组码的生成多项式及构成多项式。本发明较好地解决了RS码分组长度确定，分组起始点确定及RS码生成多项式、构成多项式确定等问题，仅通过通信内容即可实现RS码编码参数的盲识别，具有算法简捷，过程清晰，识别速度快等特点。本发明适用于智能通信、通信侦察、信息对抗等领域。CN102201883BCN10283BCN102201883B权利要求书1/1页1.一种RS码编码参数的盲识别方法，其特征在于，该方法包括如下步骤：①根据接收的数据选取合适长度的序列作为识别序列，确定将要排列的矩阵行数p，p至少大于2倍的二进制等价分组长度mn；②取定列数最大值和最小值，按列数变化将识别序列排成矩阵形式，计算该矩阵的秩，并记下秩不等于列数的列值，确定分组码长度mn；在GF(2m)上的(n，k)RS码等价(mn，mk)分组码分组长度mn的确定：对(mn，mk)线性分组码所构成的p×q矩阵，p＞2mn，q＜p，若q为mn或mn的整数倍，则单位化后左上角单位阵的维数相等，且此时矩阵的秩不等于列数q；③矩阵列数依次取为：mn，2mn，3mn，4mn……行数大于列数即可；将码序列进行移位，对各矩阵分别求秩，记下mn种移位情况时不同维数下矩阵的秩，分析确定分组码起始点；在GF(2m)上的(n，k)RS码等价(mn，mk)分组码起始点的确定：对(mn，mk)线性分组码所构成的p×q矩阵而言，其中p＞2n，q为mn倍数，当分组码起点与矩阵每行起点重合时，其秩最小，相应解空间维数最大；④从③中分析的起始点开始，将序列按a行mn列矩阵形式，其中a＞mn，即每行是一个完整的码字，对这个矩阵进行初等行变换，确定分组码的信息数mk，码率r＝k/n及校验矩阵H；⑤分析校验矩阵H，得到分组码生成多项式向量，确定m可能值；在GF(2m)上的(n，k)RS码等价(mn，mk)分组码生成多项式向量的确定：对(mn，mk)线性分组码校验矩阵H，其第mk行的第mk列到第mn列即为生成多项式向量；⑥由校验矩阵H及m，分析RS码生成多项式g(x)及构成多项式p(x)，验证识别结果正确性；验证判据如下：g(x)＝(x-αi)(x-αi+1)…(x-α2t+i-1)，其中α是构成多项式p(x)的根，通常情况下i＝0或1，2t＝n-k。2.根据权利要求1所述的RS码编码参数的盲识别方法，其特征在于，RS码包括其删余码。2CN102201883B说明书1/5页一种RS码编码参数的盲识别方法技术领域[0001]本发明涉及数字通信系统中一种RS码(包括其删余码)编码参数的盲识别方法，适用于智能通信、通信侦察、信息对抗等领域。背景技术[0002]RS码在现代通信中应用非常广泛，但是如何正确地识别出RS码编码的相关参数，从而正确解码，目前还少见报道。作为一种广泛应用于数字通信中的非二元BCH码的重要子类，RS码有不同于二进制线性分组码的特点，因而其盲识别较之一般二进制线性分组码(如Hamming码、Golay码、CRC码、一般BCH码等)有所不同，其识别应建立在符号