
BP神经网络结构优化方法.pdf

一只****ua






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

BP神经网络结构优化方法.pdf
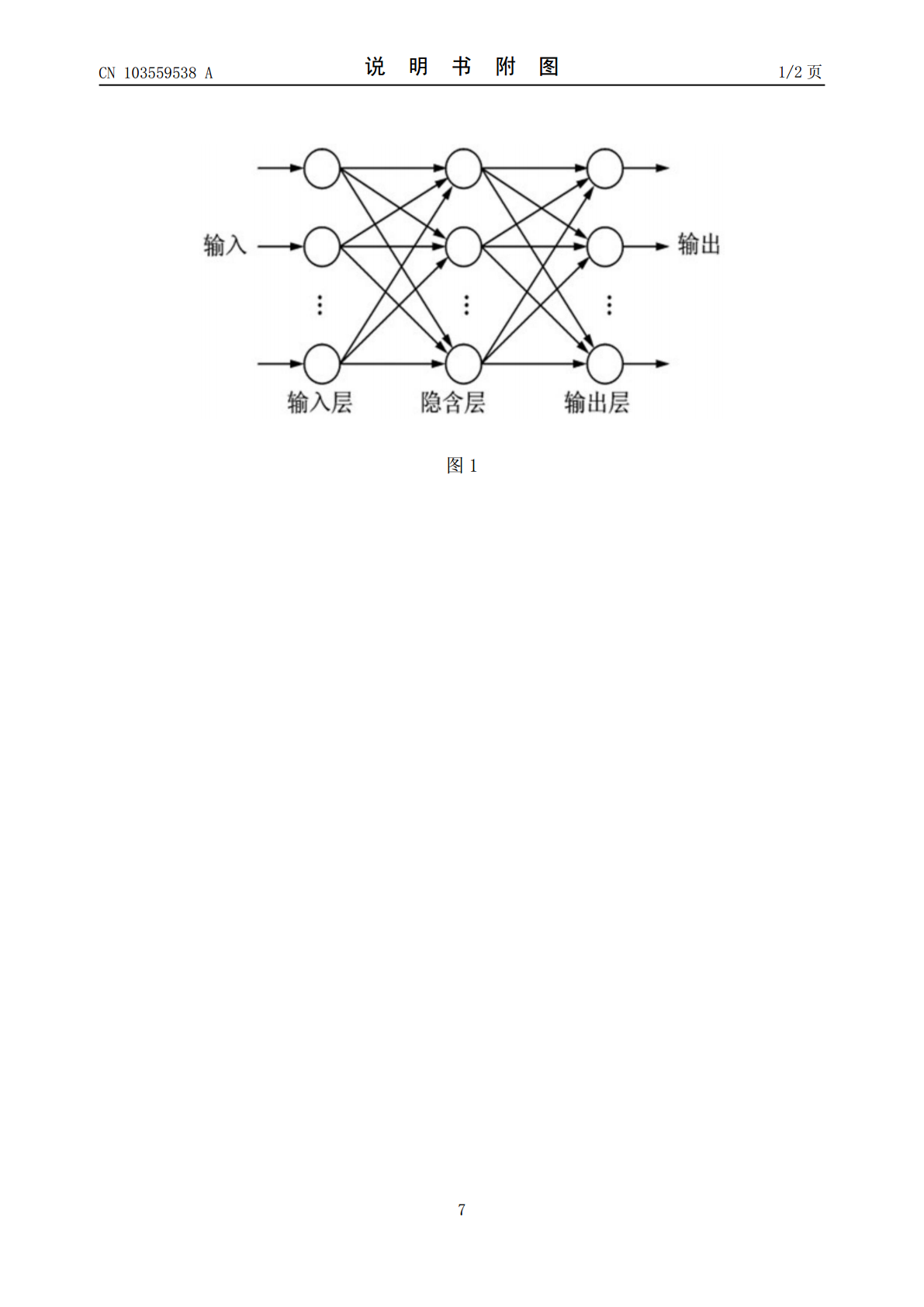
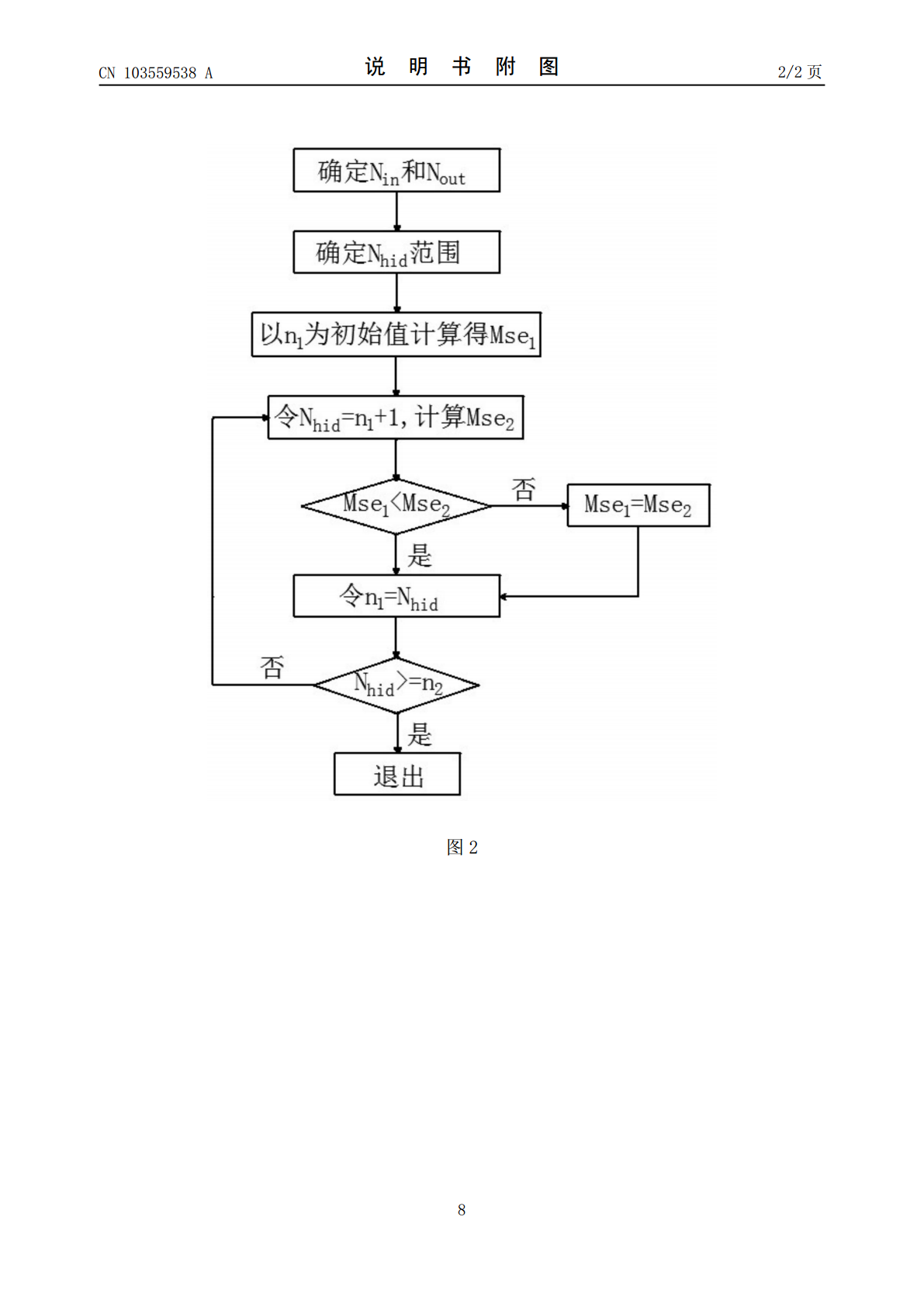
本发明提供了一种BP神经网络结构优化方法,包括如下步骤:(a)首先确定输入层神经元数目(Nin)和输出神经元数(Nout);(b)利用所述输入层神经元数目和所述输出神经元数确定所述神经网络的隐含层单元数(Nhid)的取值范围;及(c)获得所述取值范围中各值的最小均方误差(Mse),并以所述最小均方误差所对应的所述隐含层单元数(Nhid)为最佳隐含层单元数(Nhid)。本发明通过采取的在确定范围内比较均方误差来寻找最佳隐含层单元数,解决了设计三层BP神经网络结构的盲目性,避免了大量的无范围地试凑,不仅简化了

BP神经网络结构优化方法的研究及应用的中期报告.docx
BP神经网络结构优化方法的研究及应用的中期报告本文旨在介绍BP神经网络结构优化方法的研究及应用的中期报告。首先概述了BP神经网络的基本原理和常见的结构优化方法。然后介绍了本研究的主要研究内容和进展情况。BP神经网络是一种常见的人工神经网络模型,它具有学习能力和适应性,可以用于各种模式识别和分类问题。然而,传统的BP神经网络模型存在一些缺陷,如容易过拟合、学习速度慢等。因此,为了提高BP神经网络的性能,研究人员提出了各种改进方法,包括结构优化、参数优化和算法优化。结构优化是一种常见的BP神经网络改进方法,它

BP神经网络结构优化方法的研究及应用的开题报告.docx
BP神经网络结构优化方法的研究及应用的开题报告一、研究背景BP神经网络是一种常用的人工神经网络模型,常常被用于分类、回归等问题的解决。在实际应用中,如何优化BP神经网络结构,提高预测准确率,是一个热点和难点问题。因此,研究BP神经网络结构优化方法,能够在实际应用中提升其性能,具有重要意义。二、研究内容(1)对BP神经网络的结构进行分析,研究其模型特点和参数选择方法;(2)研究经典的BP神经网络结构优化方法,并分析其局限性;(3)提出一种基于遗传算法的BP神经网络结构优化方法,并分析其优势和应用场景;(4)

BP神经网络结构优化方法的研究及应用的任务书.docx
BP神经网络结构优化方法的研究及应用的任务书任务书:BP神经网络结构优化方法的研究及应用一、任务背景:随着科技的不断进步,人们对于神经网络的研究日益深入。神经网络是一种模拟生物神经网络的计算模型,具有自适应和学习能力,已被广泛应用于各种领域。BP神经网络是其中较为常见的一种,通常用于解决分类、预测、识别等问题。然而,BP神经网络的优化方法仍然是研究的热点问题。尤其是在神经网络结构方面的优化,仍存在很多挑战和困难。因此,探索BP神经网络结构优化方法,具有重要意义和应用价值。二、任务目标:本研究旨在探索BP神

神经网络优化方法bp算法缺陷.pptx
第3章神经网络优化方法3.1BP网络学习算法改进3.1BP网络学习算法改进3.1BP网络学习算法改进3.1BP网络学习算法改进3.1BP网络学习算法改进3.1BP网络学习算法改进3.1.1消除样本输入次序影响改进算法3.1.1消除样本输入次序影响改进算法3.1.2附加动量改进算法3.1.3采取自适应调整参数改进算法3.1.4使用弹性方法改进算法3.1.5使用拟牛顿法改进算法3.1.6基于共轭梯度法改进算法3.1.6基于共轭梯度法改进算法3.1.7基于Levenberg-Marquardt法改进算法BP神经
