基于稀疏理论的谐波组合信号非均匀欠采样盲重构方法.pdf

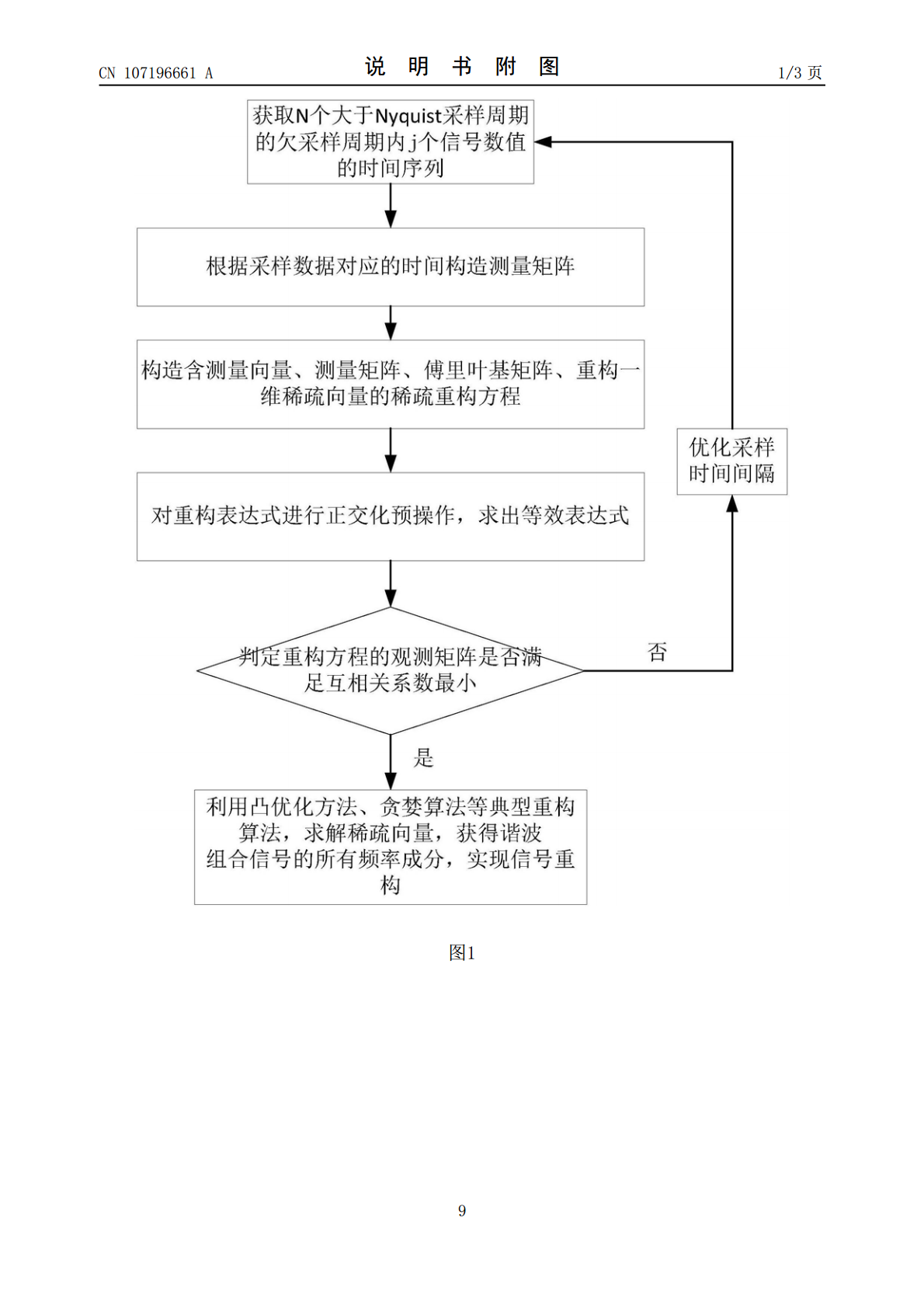
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN107196661A(43)申请公布日2017.09.22(21)申请号201710356106.9(22)申请日2017.05.16(71)申请人中国人民解放军国防科学技术大学地址410073湖南省长沙市开福区德雅路109号(72)发明人杨拥民潘明昊官凤娇胡海峰陈仲生徐海龙周畅祎(74)专利代理机构北京律谱知识产权代理事务所(普通合伙)11457代理人罗建书(51)Int.Cl.H03M7/30(2006.01)权利要求书2页说明书5页附图3页(54)发明名称基于稀疏理论的谐波组合信号非均匀欠采样盲重构方法(57)摘要本发明公开了一种非均匀欠采样条件下谐波组合信号的重构方法，其中方法包括以下步骤：步骤1、获取N个大于Nyquist采样周期的欠采样周期内j个信号数值的时间序列。步骤2、根据采样数据对应的时间构造测量矩阵。步骤3、构造含测量向量、测量矩阵、傅里叶基矩阵、重构一维稀疏向量的稀疏重构方程。步骤4、对重构表达式进行正交化预操作，构造等效表达式。步骤5、计算重构方程的观测矩阵互相关系数，调整采样时间间隔，重新构造观测矩阵，使观测矩阵互相关系数最小。步骤6、利用凸优化方法、贪婪算法等典型重构算法，求解稀疏向量，获得谐波组合信号的所有频率成分，实现信号重构。本发明提供的方法重构概率大、精度高，可以在无先验信息条件下实现谐波组合信号的盲重构。CN107196661ACN107196661A权利要求书1/2页1.一种基于稀疏理论的谐波组合信号非均匀欠采样盲重构方法，其特征在于包括以下步骤：步骤S100：获取N个大于Nyquist采样周期的欠采样周期Tn内j个信号数值的非均匀欠采样时间序列；其中，谐波组合信号非均匀欠采样时间序列的获取；包括以下步骤：步骤S101：确定一个虚拟采样间隔Tn/L；其中：L为对每个欠采样周期Tn进行等分的份数，使得等分后的时间间隔Tn/L满足Nyquist采样定理，即虚拟采样频率不低于两倍的待测信号最高频率且各个采样数据的采样时间均对应某个等分点的时刻；步骤S102：将谐波组合信号的非均匀欠采样模型表示为公式：其中r(t)为真实信号，y[tj]为采样结果的时间序列，δ(t)为狄里克莱函数，L为对欠采样周期Tn的切分倍数，ξi为一个小于L的随机正整数，决定每个周期采样的非均匀性，I为每个采样周期Tn内的采样个数，N为采样周期数；步骤S200：根据采样数据对应的时间构造测量矩阵Φp×q其具体包括以下步骤：步骤S201：确定测量矩阵的阶数；测量矩阵Φp×q的行、列数选取满足以下公式：其中p为测量矩阵的行数，与测量向量维度相同；q为测量矩阵的列数；步骤S202：测量矩阵按以下原则构造：测量矩阵Φp×q满足以下形式：其中，矩阵每行均有且只有一个元素为1，即其他元素均为0；该非零元素的坐标可表示为且1元素对应的列坐标k满足其中tj为步骤S102所提公式的第j,j≤q个采样数据的采样时刻；步骤S300：构造含测量向量y、测量矩阵Φ、傅里叶基矩阵ΨFFT、重构一维稀疏向量θ的稀疏重构方程p×1p×qq×q其中y∈R为时间序列y[tj]的向量形式、Φ∈Z为测量矩阵、ΨFFT∈C为傅里叶基矩阵、θ(f)∈Cq为重构的一维稀疏向量，该向量等效可等效成真实信号的频谱；步骤S400：对S300中的稀疏重构方程进行正交化预操作，构造等效表达式z＝Qθ(f)，其中，z∈Rp和Q∈Cp×q分别是y∈Rp和的正交化预变换表示；步骤S500:计算重构方程的观测矩阵互相关系数μ(Q)，调整采样时间间隔，重新构造等效观测矩阵Q，使观测矩阵Q互相关系数最小；2CN107196661A权利要求书2/2页其中，qi、qj是矩阵Q中的列向量；步骤S600:利用包括凸优化方法、贪婪算法在内的典型重构算法，求解稀疏向量θ，获得谐波组合信号的所有频率成分，实现信号重构。2.根据权利要求1所述的基于稀疏理论的谐波组合信号非均匀欠采样盲重构方法，其特征在于，对S300中的稀疏重构方程进行正交化预操作的步骤包括：步骤S401：构造测量向量的正交化预变换矩阵其中，为R的伪逆矩阵，Q＝orth(RT)T步骤S402：构造正交化预处理后的重构方程z＝Qθ(f)，其中，z＝Ty。3CN107196661A说明书1/5页基于稀疏理论的谐波组合信号非均匀欠采样盲重构方法技术领域[0001]本发明涉及转子振动监测系统中的信号处理技术，特别涉及一种谐波组合信号的信号重构方法。背景技术[0002]信号的稀疏性在现实世界中是广泛存在的，例如：当选取特定的小波基时，分段平滑信号的分解呈现一定的稀疏性；平滑信号在傅立叶基下的分解结果呈现稀疏性。稀疏信号重构是指利用信号的稀疏性，通过少量的线性测量值重构稀疏信号