一种容误码的系统卷积码盲识别方法.pdf

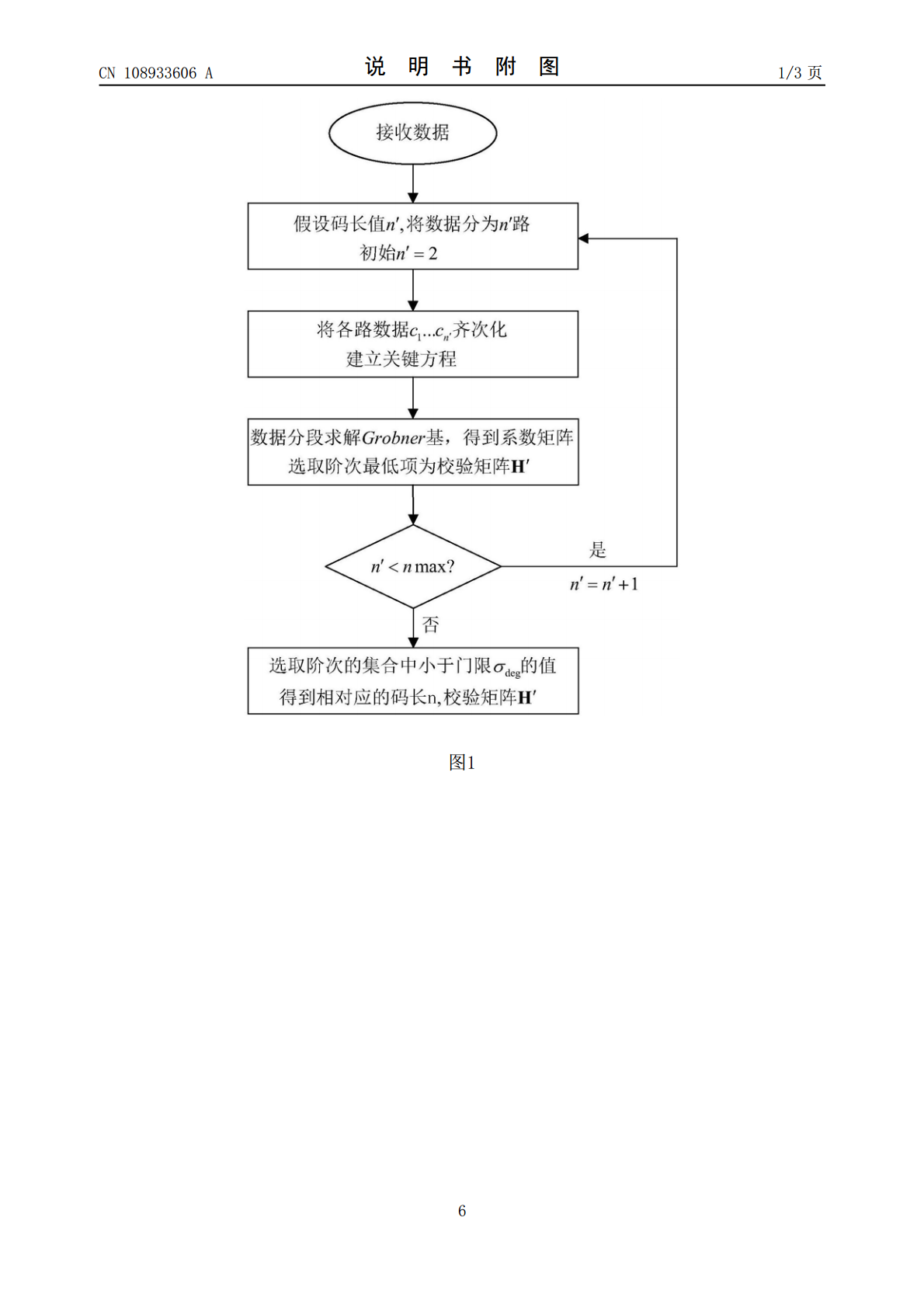
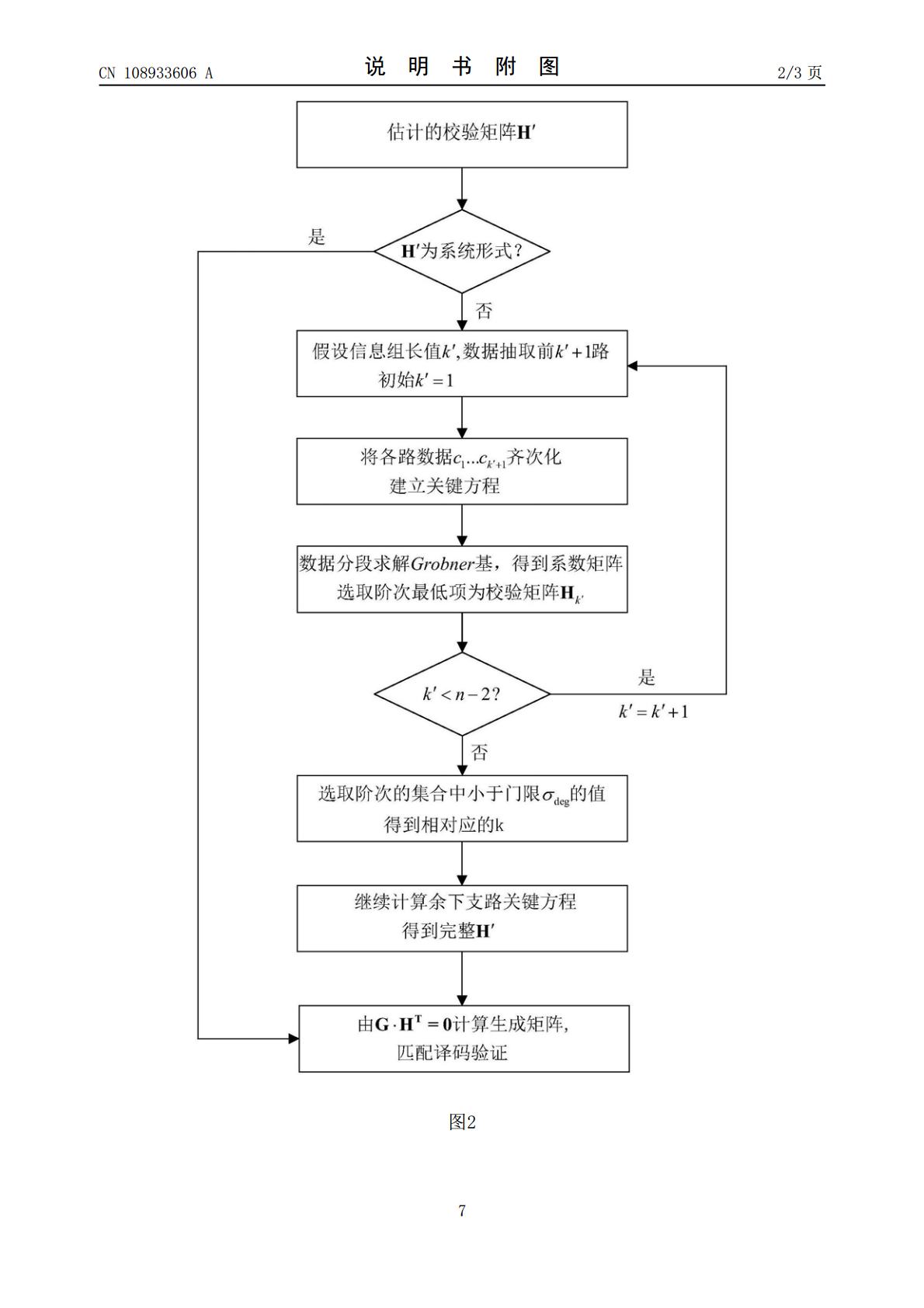
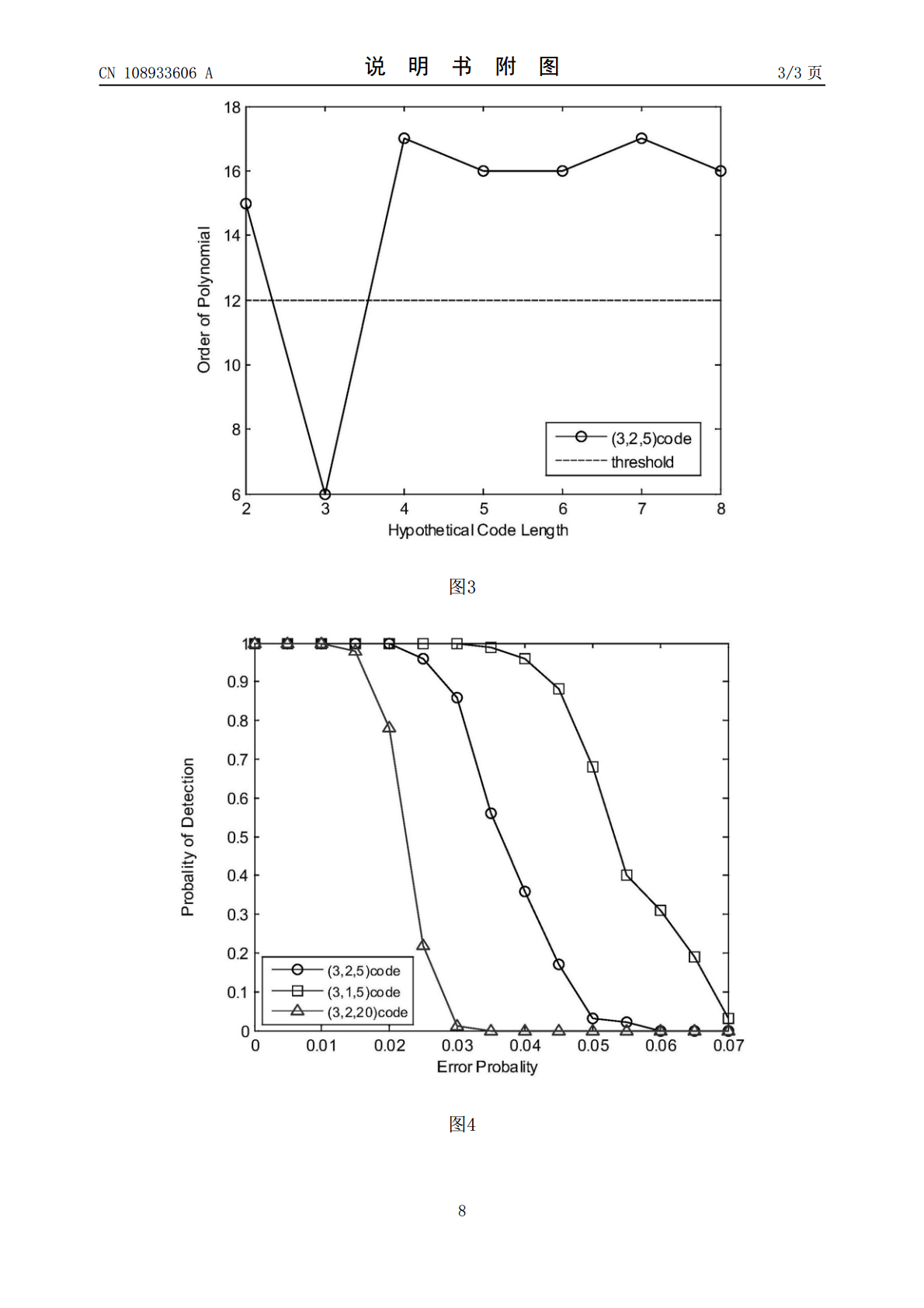
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN108933606A(43)申请公布日2018.12.04(21)申请号201810930022.6(22)申请日2018.08.15(71)申请人电子科技大学地址611731四川省成都市高新西区西源大道2006号(72)发明人宫春涛马俊虎廖红舒甘露(74)专利代理机构成都点睛专利代理事务所(普通合伙)51232代理人孙一峰(51)Int.Cl.H03M13/23(2006.01)权利要求书1页说明书3页附图3页(54)发明名称一种容误码的系统卷积码盲识别方法(57)摘要本发明属于通信技术领域，涉及一种容误码的系统卷积码盲识别方法。首先在非1/2码率下推广了求解关键方程的识别算法，利用正确解的系数矩阵阶数与错误解的系数矩阵阶数关系判别得到码率。采用校验矩阵恢复得到生成矩阵，完成了系统卷积码的参数估计。算法采取多段数据综合分析求解校验矩阵，具有容误码性能，且适用于约束长度较大的系统卷积码。CN108933606ACN108933606A权利要求书1/1页1.一种容误码的系统卷积码盲识别方法，该方法用于在误码环境下识别k/n码率的系统卷积码，其特征在于，包括以下步骤：S1、估计卷积码码长n：S11、假设码长值n′，初始为2，将数据序列抽取为n′路c1...,cn′；N+1N+1S12、将各路数据c1...,cn′齐次化，最高次记为N，I＝<x，y>；建立Γ＝{(h1,h2...,2hn′)∈F[x,y]|h1c1(x,y)+h2c2(x,y)+...+hn′cn′(x,y)≡0modI}；(n)(n)S13、数据分段采用sy2sy双合算法求解Grobner基，得到系数矩阵{A1,A2...,A(n)(n)n′+2}，选取阶次最低项为校验矩阵Hn′，记录阶次degn′；S14、若n′小于设定的最大码长nmax，n′＝n′+1，跳回S11步继续遍历；若遍历完毕，选取(n)(n)(n)阶次的集合{deg2,deg3...,degn′}中小于门限σdeg的值，得到相对应的码长n,校验矩阵H′；S2、估计信息子组长k与生成矩阵G：S21、若G′为系统形式，k′＝n-1，由G·HT＝0，通过H′求得对应的G′,之后进行S26；否则进行S22-S26；S22、假设信息子组长值k′，初始为1，选取前k′+1路数据c1...ck′+1；，N+1N+1S23、将各路数据c1...,ck′+1齐次化，最高次记为N，I＝<x，y>；建立Γ＝{(h1,h2...,2hk′+1)∈F[x,y]|h1c1(x,y)+h2c2(x,y)+...+hk′+1ck′+1(x,y)≡0modI}；(k)(k)S24、数据分段采用sy2sy双合算法求解Grobner基，得到系数矩阵{A1,A2...,A(k)(k)k′+3}，选取阶次最低项为校验矩阵Hk′，记录阶次degk′；S25、若k′小于n-2，k′＝k′+1，跳回S23步继续遍历；若遍历完毕，选取阶次的集合{deg(k)(k)(k)1,deg2...,degn-2}中小于门限σdeg的值，得到相对应的信息子组长k；依次选取余下的支路通过关键方程求解完整的校验矩阵H，通过H求得对应的G；S26、使用G′对序列进行匹配译码，若一致性大于门限σT，则，G＝G′。2CN108933606A说明书1/3页一种容误码的系统卷积码盲识别方法技术领域[0001]本发明属于通信技术领域，涉及一种容误码的系统卷积码盲识别方法。背景技术[0002]卷积码作为一种具有良好纠错能力的信道编码，近年来在通信领域已获得广泛应用。卷积码参数的盲识别技术成为了信息对抗中的关键问题，国内外对其编码参数的识别技术研究也逐渐深入。[0003]将信源序列的k个码元为一组，经寄存器长度为m的编码器编码得到n个输出码字，构成了参数为(n,k,m)的卷积码序列。按照编码规则划分，卷积码可以分为系统卷积码与非系统卷积码。[0004]识别其生成矩阵，可以得到卷积码的编码参数。但是，在信道传输中因为噪声影响产生误码，使得识别难度大大提升。目前存在的检测算法主要有下面几种方法：(1)矩阵变换法，该方法根据卷积码类似分组码的性质，通过矩阵变换得到卷积码的参数。该方法具有较好的盲估计性和通用性，由于矩阵变换不容错，其容错性有待进一步研究。(2)邹艳、陆佩忠等人提出了基于对关键方程推广的双合冲算法，该方法利用齐次关键模方程(HKME)实现了1/2码率卷积码生成多项式矩阵的快速识别，但对卷积码的码率有限制条件。(3)刘健等人提出了Walsh-Hadamard分析法，该方法采用Walsh-Hadamard变换求解方程组，来得到码率卷积码的生成多项式矩阵。该方法具有较好的容错性，但需要知道码率、编码存