高考数学总复习 第四单元 第三节 导数的应用Ⅱ课件.ppt

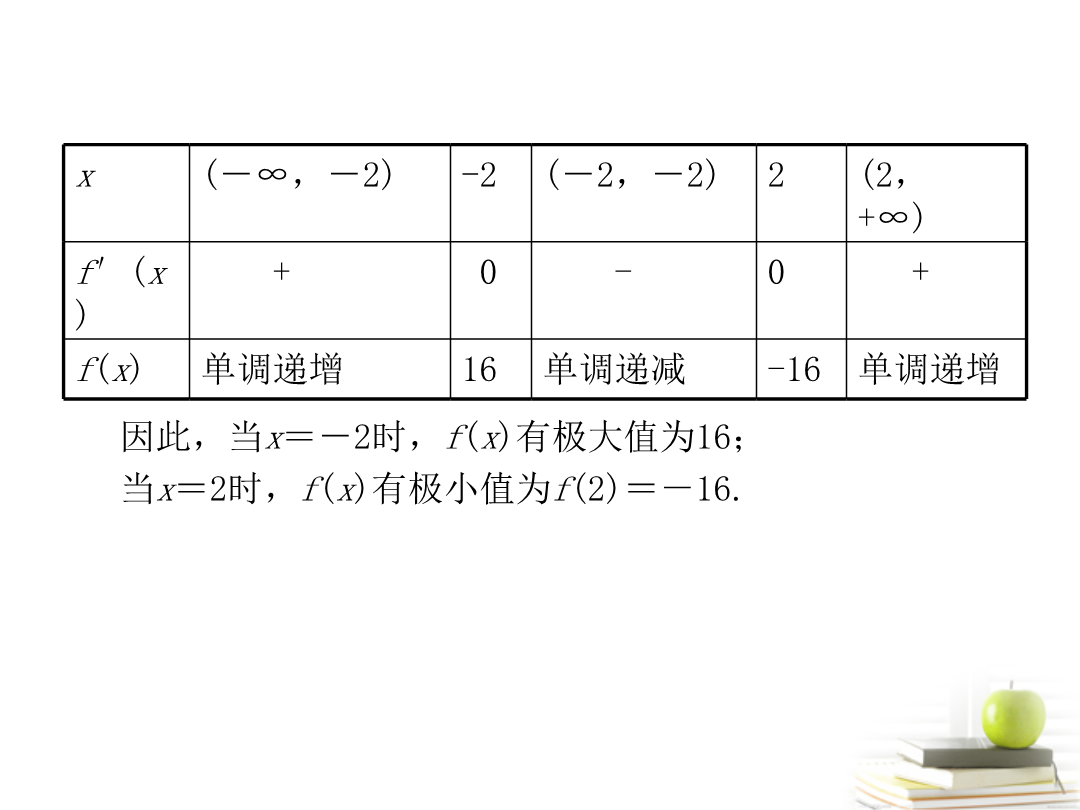
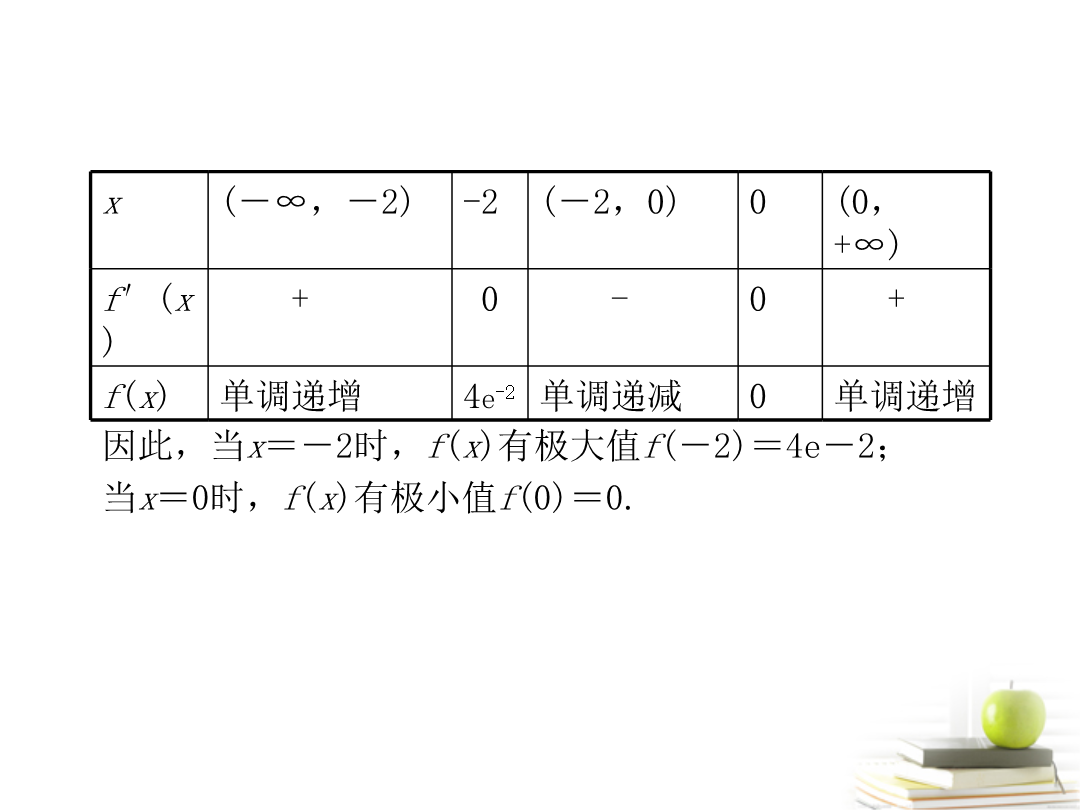
第三节导数的应用Ⅱ求函数的极值分析首先从方程f′(x)＝0求在函数f(x)定义域内所有可能的极值点然后按照函数极值的定义判断在这些点处是否取得极值．解f′(x)＝3x2－12＝3(x＋2)(x－2)令f′(x)＝0解得x＝－2或x＝2.当f′(x)＞0时x＜－2或x＞2；当f′(x)＜0时－2＜x＜2.故当x变化时f′(x)f(x)的变化情况如下表：x规律总结求可导函数f(x)极值的步骤：(1)确定函数的定义域；(2)求导数f′(x)；(3)求方程f′(x)＝0的根；(4)检验f′(x)在方程f′(x)＝0的根的左右两侧的符号如果在根的左侧附近f′(x)＞0右侧附近f′(x)＜0那么函数y＝f(x)在这个根处取得极大值；如果在根的左侧附近f′(x)＜0右侧附近f′(x)＞0那么函数y＝f(x)在这个根处取得极小值．变式训练1求函数f(x)＝x2ex的极值．【解析】函数的定义域为Rf′(x)＝2xex＋x2ex＝x(x＋2)ex.令f′(x)＝0解得x＝－2或x＝0.当x变化时f′(x)f(x)的变化情况如下表：x利用函数极值求参数的问题分析本题考查函数极值的概念考查运用导数研究函数性质的方法．首先借助极值点求出函数的解析式再利用导数求出函数的极值．解f′(x)＝3ax2＋2bx－3.依题意得f′(1)＝f′(－1)＝0即解得∴f(x)＝x3－3xf′(x)＝3x2－3＝3(x＋1)(x－1)．令f′(x)＝0得x＝－1或x＝1.若x∈(－∞－1)∪(1＋∞)则f′(x)＞0∴f(x)在(－∞－1)和(1＋∞)上是增函数若x∈(－11)则f′(x)＜0∴f(x)在(－11)上是减函数．∴f(－1)＝2是极大值f(1)＝－2是极小值．规律总结注意多项式可导函数的极值点与导数为零的根之间关系的应用变式训练2设函数f(x)＝2x3＋3ax2＋3bx＋8c在x＝1及x＝2时取得极值．(1)求a、b的值；(2)若对于任意的x∈[03]都有f(x)＜c2成立求c的取值范围．【解析】(1)f′(x)＝6x2＋6ax＋3b∵函数f(x)在x＝1及x＝2时取得极值∴f′(1)＝0f′(2)＝0即解得a＝－3b＝4.(2)由(1)可知f(x)＝2x3－9x2＋12x＋8cf′(x)＝6x2－18x＋12＝6(x－1)(x－2)．当x∈[01)时f′(x)＞0；当x∈(12)时f′(x)＜0；当x∈(23]时f′(x)＞0.∴当x＝1时f(x)取得极大值f(1)＝5＋8c.又f(0)＝8cf(3)＝9＋8c∴当x∈[03]时f(x)的最大值为f(3)＝9＋8c.∵对于任意的x∈[03]有f(x)＜c2恒成立∴9＋8c＜c2解得c＜－1或c＞9∴c的取值范围为(－∞－1)∪(9＋∞)．求函数的最值∴函数f(x)的单调增区间是(－∞－)(＋∞)．∵f(－1)＝10f()＝－8f(3)＝18∴f(x)在[－13]上的最大值是f(3)＝18最小值是f()＝－8规律总结求可导函数在[ab]内的最大值和最小值的步骤：(1)求函数f(x)在(ab)内的极值；(2)求f(x)在区间端点的值f(a)f(b)；(3)将函数f(x)的各极值与f(a)f(b)比较其中最大的一个为最大值最小的一个为最小值．变式训练3已知函数f(x)＝x－lnx求f(x)在区间[1e]上的值域其中e＝2.71828…是自然对数的底数．【解析】令f′(x)＝0得x＝1.∵f(1)＝1f(x)在(1＋∞)上递增∴f(x)max＝f(e)＝e－1.∴f(x)在区间[1e]上的值域为[1e－1]．导数的综合应用统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比；比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比比例系数为k.当垃圾处理厂建在弧AB的中点时对城A和城B的总影响度为0.065.(1)将y表示成x的函数；(2)讨论(1)中函数的单调性并判断弧AB上是否存在一点使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在求出该点到城A的距离；若不存在说明理由分析(1)总影响度y为C厂对城A和对城B影响度之和所以分别表示出C厂对城A和对城B的影响度．从而求出函数表达式．(2)求函数的最小值解(1)当点C在弧AB中点时|AC|＝10C厂对城A影响