预览加载中，请您耐心等待几秒...

高中数学 335函数的极值与导数课件 新人教A版选修1 1 课件.ppt

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共14页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

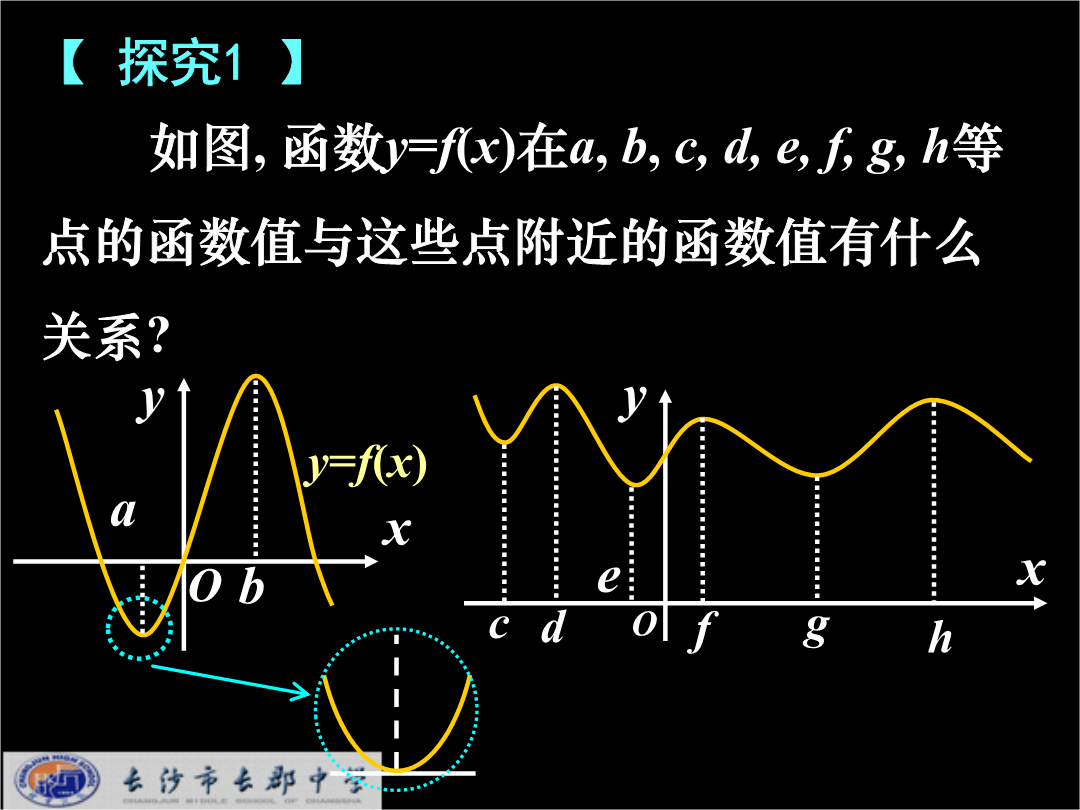
一、温故知新2.用导数法讨论函数单调区间的基本步骤:如图函数y=f(x)在abcdefgh等点的函数值与这些点附近的函数值有什么关系?1、极值点与极值的概念我们把点a叫做函数y=f(x)的极小值点f(a)叫做函数y=f(x)的极小值;点b叫做函数y=f(x)的极大值点f(b)叫做函数y=f(x)的极大值.极小值点、极大值点统称为极值点极大值和极小值统称为极值。【注】（1）极值反映了函数在某一点附近的大小情况刻画的是函数的局部性质.（2）函数的极大值一定大于函数的极小值吗？【注】（1）极值反映了函数在某一点附近的大小情况刻画的是函数的局部性质；（2）函数的极值不是唯一的；（3）函数的极大值不一定大于函数的极小值。y=f(x)在这些点的导数值是多少?在这些点附近y=f(x)的导数的符号有什么规律?【归纳】【归纳】【归纳】[例1]求函数f(x)=x3－4x+4的极值.[变式训练]已知f(x)=x3+3ax2+bx+a2在x=-1处有极值0求常数ab的值.一般地求函数y=f(x)的极值的方法是: