
中考数学复习课件:几何型综合问题 课件.ppt

子璇****君淑








亲,该文档总共21页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

中考数学复习课件:几何型综合问题 课件.ppt
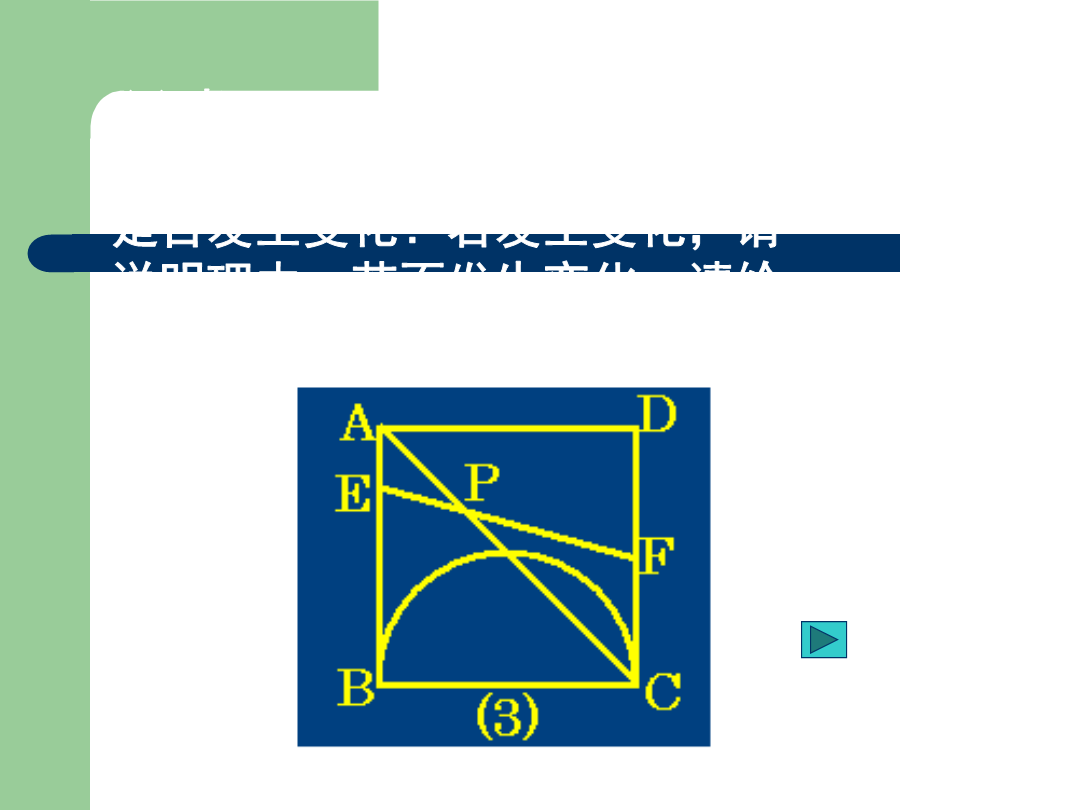
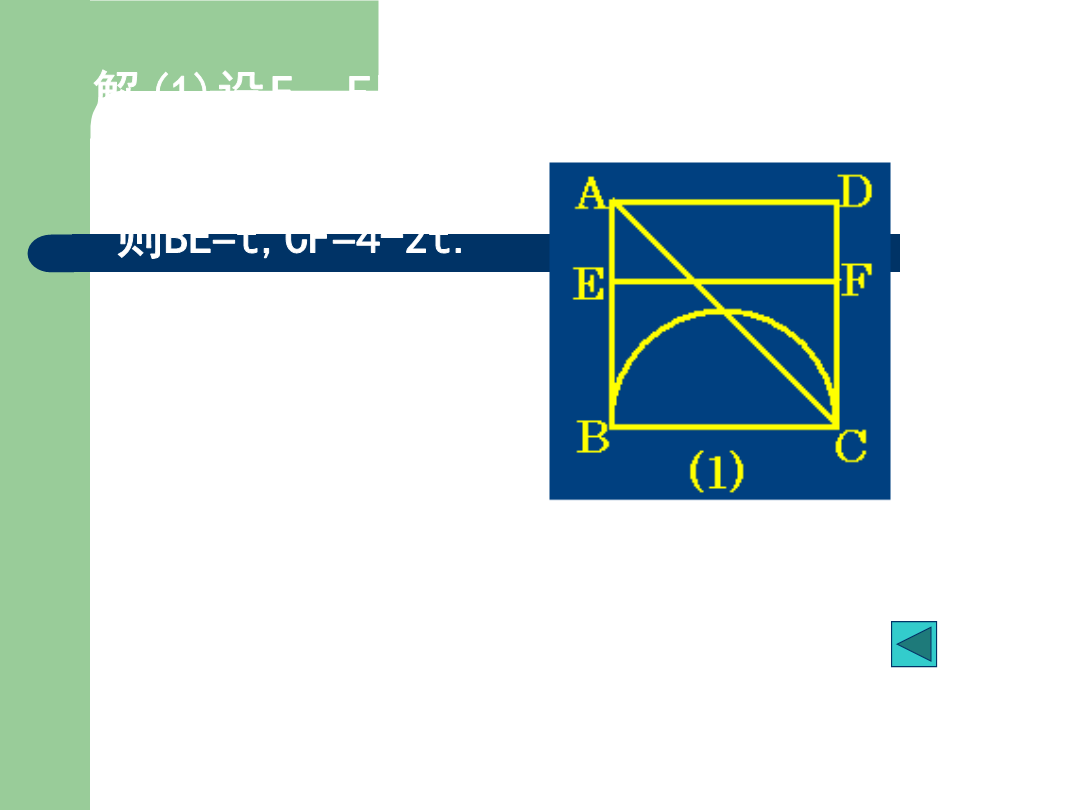
动态几何问题[例1](南昌市2001)如图示正方形ABCD中有一直径为BC的半圆BC=2cm现有两点E、F分别从点B、A同时出发点E沿线段BA以1cm/秒的速度向点C运动点F沿折线A-D-C以2cm/秒的速度向点C运动设点E离开点B的时间为t秒。(1)当t为何值时线段EF与BC平行?(2)设1<t<2时当t为何值时EF与半圆相切?(3)当1≤t<2时设EF与AC相交于点P问点E、F运动时点P的位置是否发生变化?若发生变化请说明理由;若不发生变化请给予证明并求AP:PC的值。解(1)设E、F出发后

课件-全国-2009_中考数学复习课件:几何型综合问题.rar
动态几何问题[例1](南昌市,2001)如图示,正方形ABCD中,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、A同时出发,点E沿线段BA以1cm/秒的速度向点C运动,点F沿折线A-D-C以2cm/秒的速度向点C运动,设点E离开点B的时间为t秒。(1)当t为何值时,线段EF与BC平行?(2)设1<t<2时,当t为何值时,EF与半圆相切?(3)当1≤t<2时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP:PC的

中考数学几何型综合问题课件新人教版 课件.ppt
动态几何问题[例1](南昌市2001)如图示正方形ABCD中有一直径为BC的半圆BC=2cm现有两点E、F分别从点B、A同时出发点E沿线段BA以1cm/秒的速度向点C运动点F沿折线A-D-C以2cm/秒的速度向点C运动设点E离开点B的时间为t秒。(1)当t为何值时线段EF与BC平行?(2)设1<t<2时当t为何值时EF与半圆相切?(3)当1≤t<2时设EF与AC相交于点P问点E、F运动时点P的位置是否发生变化?若发生变化请说明理由;若不发生变化请给予证明并求AP:PC的值。解(1)设E、F出发后

初中数学复习课件:几何型综合问题(2).ppt
动态几何问题[例1](南昌市,2001)如图示,正方形ABCD中,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、A同时出发,点E沿线段BA以1cm/秒的速度向点C运动,点F沿折线A-D-C以2cm/秒的速度向点C运动,设点E离开点B的时间为t秒。(1)当t为何值时,线段EF与BC平行?(2)设1<t<2时,当t为何值时,EF与半圆相切?(3)当1≤t<2时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP:PC的

初中数学复习课件:几何型综合问题(2).ppt
动态几何问题[例1](南昌市,2001)如图示,正方形ABCD中,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、A同时出发,点E沿线段BA以1cm/秒的速度向点C运动,点F沿折线A-D-C以2cm/秒的速度向点C运动,设点E离开点B的时间为t秒。(1)当t为何值时,线段EF与BC平行?(2)设1<t<2时,当t为何值时,EF与半圆相切?(3)当1≤t<2时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP:PC的
