4直接证明与间接证明课件 新人教A版 课件.ppt

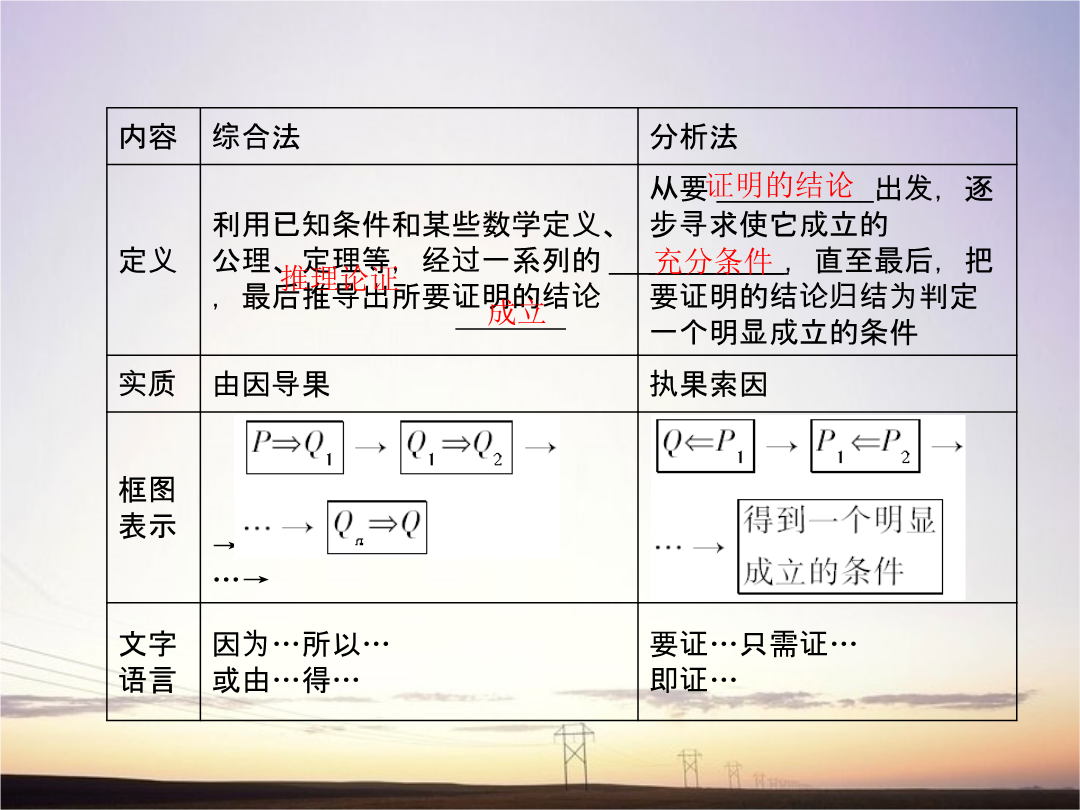
1．直接证明内容综合法和分析法有什么区别与联系？提示：分析法的特点是：从“未知”看“需知”逐步靠拢“已知”其逐步推理实际上是寻求它的充分条件；综合法的特点是：从“已知”看“可知”逐步推向“未知”其逐步推理实际上是寻找它的必要条件．分析法与综合法各有其特点有些具体的待证命题用分析法或综合法均能证明出来往往选择较简单的一种.2.间接证明反证法：假设原命题(即在原命题的条件下结论不成立)经过正确的推理最后得出因此说明假设错误从而证明了原命题成立这样的证明方法叫反证法．答案：A答案：B3．用反证法证明命题：若整系数一元二次方程ax2＋bx＋c＝0(a≠0)有有理数根那么a、b、c中至少有一个是偶数时下列假设中正确的是()A．假设a、b、c都是偶数B．假设a、b、c都不是偶数C．假设a、b、c至多有一个偶数D．假设a、b、c至多有两个偶数答案：B4．设a、b、c∈(0＋∞)P＝a＋b－cQ＝b＋c－aR＝c＋a－b则“PQR>0”是“P、Q、R同时大于零”的()A．充分而不必要条件B．必要而不充分条件C．充分且必要条件D．即不充分又不必要条件解析：必要性是显然成立的当PQR>0时若P、Q、R不同时大于零则其中两个为负一个为正不妨设P>0Q<0R<0则Q＋R＝2c<0这与c>0矛盾即充分性也成立．答案：C当要证的不等式较复杂两端差异难以消除或者已知条件信息量太少已知与待证间的联系不明显时一般可采用分析法分析法是步步寻求不等式成立的充分条件而实际操作时往往是先从要证的不等式出发寻找使不等式成立的必要条件再考虑这个必要条件是否充分这种“逆求”过程能培养学生的发散思维能力也是分析问题、解决问题时常用的思考方法.证明：要证只需证b2－ac<3a2∵a＋b＋c＝0只需证b2＋a(a＋b)<3a2只需证2a2－ab－b2>0只需证(a－b)(2a＋b)>0只需证(a－b)(a－c)>0.因为a>b>c所以a－b>0a－c>0所以(a－b)(a－c)>0显然成立故原不等式成立思路分析：题目中出现了“不是”这个词语要直接去进行解答会有困难通常用反证法来证明．本题若用直接法证明难以入手用反证法证明假设数列{an}是等比数列得出矛盾即可．题目中如果出现“不是”“至少”“不可能”等词语时通常采用反证法证明.变式迁移3已知a、b、c是互不相等的非零实数．求证：三个方程ax2＋2bx＋c＝0bx2＋2cx＋a＝0cx2＋2ax＋b＝0至少有一个方程有两个相异实根．证明：假设三个方程中都没有两个相异实根则Δ1＝4b2－4ac≤0Δ2＝4c2－4ab≤0Δ3＝4a2－4bc≤0相加有a2－2ab＋b2＋b2－2bc＋c2＋c2－2ac＋a2≤0即(a－b)2＋(b－c)2＋(c－a)2≤0.①由题意a、b、c互不相等∴①式不成立．∴假设不成立即三个方程中至少有一个方程有两个相异实根．【例4】已知常数a>0n为正整数fn(x)＝xn－(x＋a)n(x>0)是关于x的函数．(1)判定函数fn(x)的单调性并证明你的结论；(2)对任意n>a证明f′n＋1(n＋1)<(n＋1)f′n(n)．证明：(1)f′n(x)＝nxn－1－n(x＋a)n－1＝n[xn－1－(x＋a)n－1]∵a>0x>0∴f′n(x)<0∴fn(x)在(0＋∞)上单调递减．(2)由(1)知当x>a>0时fn(x)＝xn－(x＋a)n是关于x的减函数∴当n≥2时有(n＋1)n－(n＋1＋a)n<nn－(n＋a)n.又∵f′n＋1(x)＝(n＋1)[xn－(x＋a)n]∴f′n＋1(n＋1)＝(n＋1)[(n＋1)n－(n＋1＋a)n]<(n＋1)[nn－(n＋a)n]＝(n＋1)[nn－(n＋a)(n＋a)n－1]．(n＋1)f′n(n)＝(n＋1)n[nn－1－(n＋a)n－1]＝(n＋1)[nn－n(n＋a)n－1]∵n＋a>n∴f′n＋1(n＋1)<(n＋1)f′n(n)．解：(1)∵f′(x)＝ax2＋2bx＋c由题意及导数的几何意义得f′(1)＝a＋2b＋c＝0①f′(m)＝am2＋2bm＋c＝－a②由a<b<c可得4a<a＋2b＋c<4c即4a<0<4c故a<0c>0由①得c＝－a－2b代入a<b<c再由a<01．关于综合法与分析法(1)综合法是“由因导果”．它是从已知条件出发顺着推证．用综合法证明命题的逻辑关系是：A⇒B1⇒B2⇒…⇒Bn⇒B(A为已经证明过的结论B为要证明的结论．它的常见书面表达是“∵∴”或“⇒”．(2)分析法是“执果索因”一步步寻求上一步成立的充分条件．它是从要求证的结论出发倒着分析由未知想需知由需知逐渐地靠近已知(已知条件已经学过的定义、定理、公理、公式、法则等)．用分析法证明命题的逻辑关系是：B⇐B1⇐B2…⇐Bn⇐A.它的常